摘要
在本文中,我们提出并讨论了先导电流、电荷、速度和先导传播模式之间的关系。 通过使用能量考虑,我们建立了一个数学表达式,该表达式只需要物理参数,并允许人们评估前导的速度或前导传播过程中消耗的能量的小数部分 β。 获得的 β 值给出的先导速度在形状和幅度上与长气隙放电的实验测量结果非常一致。
1. 引言
使用模型来帮助物理理解空气放电并预测对电气工程有用的值,其历史几乎与研究击穿现象本身一样长。 非均匀场中的正先导形成和传播已成为许多实验和理论工作的主题(Klewe 等人 1987,Les Renardières group 1977,Gallimberti 1979,Gary 等人 1984)。 已经提出了不同的模型来描述放电机制。 这些主要是定性的。 事实上,有许多不同的模型涵盖了放电过程的每个阶段,但不存在完美的模型。 它们要么是纯经验的、半经验的、半物理的,甚至是纯物理的(Klewe 等,1974)。
制作可靠模型的困难在于放电中发生的现象的复杂性。 出于连续性的目的,我们总结了构成正脉冲电压放电事件的主要时间顺序。 当电场强度达到足够高的值时,在产生适当的自由电子的时滞之后开始放电。 然后,发生第一次电离过程:这是第一次电晕。 这通常采用丝状通道或飘带的形式。 作为电晕生长的结果,净正电荷迅速注入间隙。 在日冕飘带的根部,观察到一个短的明亮通道(茎)。 放电的进一步发展起源于这个茎。 下一阶段取决于可能导致火花引导通道的间隙中电场的不均匀程度。 在任何情况下,先导生长通常先于二次电晕放电。 其传播速度取决于电极的几何形状和施加的电压。 平面方向前导的增长是连续的或不连续的。 当外加电压的增加率太低时,先导会逐步增长。 领导者传播的最后阶段被称为最终跳转。 这是leader传播的最后阶段,不可避免地会导致gap的短路。
已经提出了各种数学表达式(Pigini et al 1989)来关联瞬时先导速度。 这些通常取决于电压和间隙中领先者的位置。 其中一些纯粹是经验性的,仅在必须准确定义的某些条件下才有效。 由于存在偏离其有效性领域的风险,因此在处理经验模型时必须小心。
在这项工作中,我们提出了一个基于能量考虑的数学表达式,它允许人们评估传播速度或用于前导位移的动能的分数部分。 将获得的结果与其他人通过实验获得的结果进行比较。
2. 能量输入
我们使用的方法类似于 Béroual (1993) 在另一种电介质中提出的方法。 在先导的传播过程中,总能量$W_t$以不同的形式消耗:热能、电离、辐射等。$W_t$的一部分(动能)将转移到前导通道,使其延长距离$dl_j$。 称 $W_c$ 为动能,我们可以写成
\[W_c = \beta W_t \tag{1}\]β 是先导位移所需的全部能量的小数部分。 它在 0 < β ≤ 1 的范围内。
近年来,对长火花开发的理解的重大改进是基于对先导通道中发生的流体动力过程的分析(Les Renardières group 1986)。 引线在膨胀中表现为流体。 在时间 $dt$ 期间,添加到通道的质量等于气体密度 $ρ$和体积增量 ($\pi r _ { j } ^ { 2 } d l _ { j }$) 的乘积:$m = \rho \pi r _ { j } ^ { 2 } d l _ { j }$(其中$r_j$是分支 j 的半径 )。
在这项工作中,我们将假设通道新分支的半径$r_j$和后者的温度 T 是常数:$r_j = r_0$ 和 $T = T_0$
\[W _ { c } = \frac { 1 } { 2 } \rho \pi r _ { j } ^ { 2 } d l _ { j } v _ { j } ^ { 2 } \tag{2}\]其中 $v_j$是分支 j 的速度。 考虑到放电由$n$ 个步骤组成,每个步骤都可以同化为一个圆柱形通道,我们可以写出任何时间(Béroual 1993):
\[\sum _ { j = 1 } ^ { n } \frac { 1 } { 2 } ( \rho \pi r _ { j } ^ { 2 } d l _ { j } ) v _ { j } ^ { 2 } = \beta \sum _ { j = 1 } ^ { n } q _ { j } E _ { j } d l _ { j } \tag{3}\]其中 $q_j$和 $E_j$ 分别是分支 j 的电荷和其头部的电场。 因此,领导者的每个位移$dl_j$对应的速度将为
\[v _ { j } ^ { 2 } = \frac { 2 \beta } { \pi r _ { j } ^ { 2 } \rho } ( \int i _ { j } d t ) E _ { j } \tag{4}\]3. 先导的平均速度
通常,先导电流由许多离散脉冲构成(Gary et al 1984, Ortéga 1992)。 总电荷是从电流脉冲的积分中推导出来的所有基本电荷的总和(Ortéga 1992),它会随着步骤而变化。 每个基本电荷都有助于领导者的部分传播。 需要注意的是,两个连续电流脉冲之间的电流所对应的电荷相对于单个脉冲所对应的电荷可以忽略不计。
令$t_j$ 为脉冲时间$t_{pj}$与停顿时间$t_{0j}$到下一个脉冲的时间之和所对应的时间,即
\[t _ { j } = t _ { p j } + t _ { 0 j } \tag{5}\]和$v_{pj}$和 $v_{0j}$,分别是$t_{pj}$和$t_{0j}$期间的速度。 设 $v_{al}$ 是前导通过电极间隙的平均速度。 然后
\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( v _ { p j } t _ { p j } + v _ { 0 j } t _ { 0 j } ) \tag{6}\]n 是先导放电的step。
根据公式(4)
\[v _ { p j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { p j } E _ { j } \tag{7}\] \[v _ { 0 j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { 0 j } E _ { j } \tag{8}\]将(7)和(8)代入(6)中,我们得到
\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } [ ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ] \tag{9}\]$v_{0j}$通常相对于$v_{pj}$可以忽略不计。 实际上,$v _ { 0 j }$是在时间$t_{0}$期间前导器的平均速度,这是在前导器尖端重建电荷并达到允许前导器移动新一步的电场临界值所必需的。
假设 $r_j$, β, ρ 和 $E_j$ 在整个传播过程中保持不变,我们将获得领导者的平均速度如下:
\[v _ { a l } = ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ) \tag{10}\]当忽略$v_{0j}$时,我们将有
\[v _ { a l } \cong ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{11}\]似乎$E_j$和/或 $q_{pj}$ 越高,先导发展的平均速度就越高。
3.1 密度的测定
在高温下,所有气体都被认为是完美的。 由于先导是高度电离的等离子体 (T ≥ 1000 K) (Gallimberti 1979, Domens 1987),因此可以应用完美气体定律。 因此
\[p V = \frac { m } { M } R T \tag{12}\]其中 p、V、m、R、T 和 M 分别是压力、体积、通道质量、理想气体常数、温度和通道的摩尔质量。
由于密度 ρ 等于 m/V,我们得到
\[\rho = \frac { M } { R } \frac { p } { T } \tag{13}\]前导阶段是非爆炸性的,前导压力可以被认为是恒定的(Les Renardières group 1977,Domens 1987)并且大约等于大气压力(Gallimberti 1979)。 因此
\[\rho ( kg m ^ { - 3 } ) = \frac { k } { T ( K ) R } \tag{14}\]其中,$k = Mp$
在目前的情况下,R 与温度有关(Les Renardières group 1986)。 事实上,它取决于气体粒子的平均分子质量,它受 $O_2$ 和 $N_2$分子解离的影响,反之,受 O 和 N 原子重组的影响。 因此,方程 (14) 表示 ρ 和 T 之间的非线性状态关系。
3.2 先导头处的场计算
频道的结局值得怀疑。 该结束对于尖端上的合成场强 $E_j$ 是必不可少的。 $E_j$ 是通道向下增长的重要情况。 该场$E_j$ 与沿通道分布的总电荷有关。 Szpor (1971) 提出了这一假设。 可以使用双曲线近似来估计(Hutzler 和 Hutzler 1982):
\[E _ { j } = \frac { 2 U _ { j } } { R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } \tag{15}\]$L_z$和 D 分别是前导轴向长度和间隙长度,$U_j = U − \Delta U_j$是前导尖端上的电压(其中 U 是电极上施加的电压,$\Delta U_j$是沿通道的电压降)和 $R_e$ 等效电极的半径。
根据 Hutzler 和 Hutzler (1982),$R_e$ 可以表示为线性关系
\[R _ { e } = \alpha S \tag{16}\]其中 S 是拖缆长度,α 是取决于电极形状的比例系数。 通过凭经验调整 α,他们获得了令人满意的结果,其值等于 1/17。
对实验结果的分析表明,拖缆长度取决于许多参数。 当先导开始传播时,S 的值特别受阳极形状和电压增加率的影响:第一次电晕放电区域的大小决定了流光的长度(Hutzler 和 赫茨勒 1982)。 最终,第一次电晕放电区域的影响下降并最终消失。 然后,流注长度 S 取决于前导长度和“过电压系数”。 后者由比率 U j /U 0 定义,U 0 是要施加到前导尖端的电压,允许其获得与空气中的临界场相等的局部场。 已经表明(Hutzler 和 Hutzler 1982)实验结果可以正确地由以下 S 表达式表示:
\[S = \frac { U _ { j } } { U _ { 0 } } \frac { 4.25 } { 1 + ( 3.5 / L ) } + S _ { i } \operatorname { exp } ( \frac { L _ { z } } { - 0.8 S _ { i } } ) \tag{17}\]其中 $S_i$和 $L$ 分别是第一条日冕流光和前导的长度。 术语 $exp[−L_z /(0.8S_i )]$简单地解释了这样一个事实,即领导者一旦时间足够长就会“忘记”第一个日冕。 因此,只有第一项具有显着的权重。 当传播发生在最佳条件下时,U j 与U 0 有很大不同。 对于较长的前导,流光长度 S 趋向于极限形式:
\[S = \frac { 4.25 } { 1 + ( 3.5 / L ) } \tag{18}\]3.3 先导平均速度
等式 (11)、(14) 和 (15) 给出
\[v _ { a l } = ( \frac { 4 \beta T _ { 0 } U _ { j } R } { \pi r _ { 0 } ^ { 2 } k R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } ) ^ { 1 / 2 } \times ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{19}\]前导的速度似乎取决于前导尖端 $U_j$ 处的电压、其轴向长度 $L_z$ 和其他物理参数。 速度的知识需要 β 的参数。
4. 分数动能
对先导平均速度的了解使我们能够确定前导位移中使用的可用能量的平均部分。 可以根据等式 (19) 推导出通过电极间隙直到最终跳跃阶段之前的步骤的不同传播步骤的 β 值:
\[\beta = \frac { v _ { a l } ^ { 2 } \pi r _ { 0 } ^ { 2 } \rho R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { s f } } { R _ { c } } ) ] } { 4 U _ { s f } } ( \frac { \sum _ { j = 1 } ^ { n } t _ { j } } { \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) } ) ^ { 2 } \tag{20}\]$L_{sf}$和$U_{sf}$ 分别是最后一次跳跃开始时的前导长度和前导尖端上的电压。 这些可以从经验方程确定。 通过让 $U_{sf}$等于 50% 的闪络电压 ($U_{50}$),它变成 (Ortéga 1992):
\[L _ { s f } = D - \frac { U _ { 50 } - 0.15 } { 0.44 } \tag{21}\]$U_{50}$由以下经验方程确定(Ortéga 1992):
\[U _ { 50 } = \frac { 3400 } { 1 + 8 / D } \quad ( KV m ) \quad \text { for } 2 m < D < 15 m \tag{22}\] \[U _ { 50 } = 1400 + 55 D \quad ( kV m ) \quad \text { for } 15 m < D < 30 m \tag{23}\]According to Garcia and Hutzler (1974)
\[U _ { s f } = 0.15 + 0.44 h _ { s f } \tag{24}\]其中 $h_{sf}$ 是最后一次跳跃的高度。
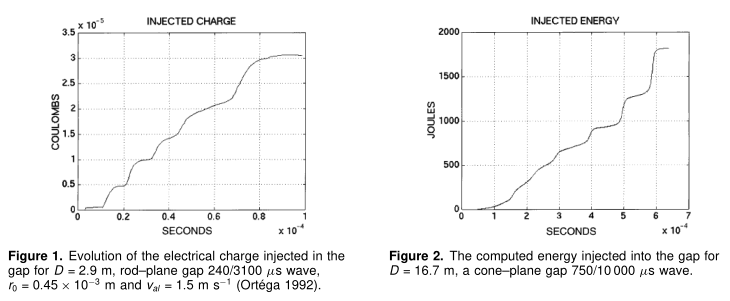
例如,让我们考虑具有电极间隙的实验数据,我们知道注入间隙的电荷形状以及 r 0 和 v al 的平均值(图 1)(Ortéga 1992)。 根据文献报道的结果,T 0 = 1000 K(Les Renardières group 1977,Gary et al 1984),因此气体密度为ρ = 0.15 kg m -3 (Les Renardières group 1986)。(Les Renardières group 1986)。 通过计算方程 (20),我们得到 D = 2.9 m,β = 0.10。
对于另一组实验数据(D = 16.7 m,锥面间隙 750/10000 µs),我们知道注入间隙的电荷形状(Domens 1987)和平均值 v al = 2 ms -1 并且r 0 = 0.5 × 10 -3 m,我们得到β = 0.09。 第一印象是几乎恒定的 β 值。 这两个例子表明,只有 10% 的总能量转化为动能。 下面我们考虑 β 的平均值:让 β = 0.10。
等式(20)表明β取决于许多参数,其中一些参数例如L sf 、V al 、D 和R e 是相互关联的。 所以,我们必须强调,温度T 0 也随着领导者的发展而变化。 由于我们只考虑前导尖端的速度,我们假设 T 0 是常数。
5. 先导的瞬时速度
根据等式(1),我们可以写成
\[d W _ { c } = \beta d W _ { t }\](假设 β 是常数)。 因此,对于每个位移 dl j ,我们将有
\[\frac { 1 } { 2 } \rho \pi r _ { j } ^ { 2 } d l _ { j } v _ { j } ^ { 2 } ( t ) = \beta d W _ { j } ( t ) \tag{25}\](dW j (t) = dW t (t) 对于步骤 j)。 由于 dl j = v j dt(dt 是步骤的持续时间),T = T 0 和 r j = r 0,我们得到
\[\frac { 1 } { 2 } \rho \pi r _ { 0 } ^ { 2 } v _ { j } ^ { 3 } ( t ) d t = \beta d W _ { j } ( t ) \tag{26}\]然后可以得到
\[v _ { j } ( t ) = ( \frac { 2 \beta } { \rho \pi r _ { 0 } ^ { 2 } } \frac { d W _ { j } ( t ) } { d t } ) ^ { 1 / 3 } \tag{27}\]或者
\[v _ { j } ( t ) = ( \frac { 2 \beta } { \rho \pi r _ { 0 } ^ { 2 } } P _ { j } ( t ) ) ^ { 1 / 3 } \tag{28}\]P j (t) 是瞬时注入功率
\[P _ { j } ( t ) = \frac { d W _ { j } ( t ) } { d t } \tag{29}\]最后,根据(14),我们将有
\[v _ { j } ( t ) = ( \frac { 2 \beta T _ { 0 } R } { k \pi r _ { 0 } } P _ { j } ( t ) ) ^ { 1 / 3 } \tag{30}\]从上面的表达式看来,W j 或P j 的知识是计算v j 所必需的。 在最近的一项工作中(Fofana 和 Béroual 1995b),我们开发了一个数学模型,使我们能够使用等效的电气网络评估引线和回程电流。 除了电流(前导和回程)外,该模型还允许我们确定相应的电荷、沿前导通道的电位降、功率和注入间隙的能量(对于给定的电压和电极配置)。