时频流形稀疏重构:一种新的轴承故障特征提取方法
Time–frequency manifold sparse reconstruction: A novel method for bearing fault feature extraction
2. 理论背景
2.1 时频流形(TFM)学习
TFM 是 TF 域中的固有非线性流形结构,嵌入到有缺陷的轴承振动信号的 TFD 上,并且可以通过在重构相空间中对一系列 TFD 进行流形学习来提取 [12,13]。 TFM结合了非平稳信息和非线性信息,因此可以针对不同的振动信号显示不同的TF模式。 关于 TFM 技术的详细信息,读者可以参考[12]。
要学习 TFM,首先应通过相空间重构 (PSR) 技术在高维相空间中重构信号的流形。 对于具有 N 个数据点的信号 x(t),m 维相空间中的第 i 个相位点向量给出为:
\[\mathbf{X}_{i}^{m}=\left[x_{i}, x_{i+\tau}, \ldots, x_{i+(m-1) \tau}\right] \tag{1}\]其中$x_i$是$x(t)$的第i点数据,m是嵌入维数,$\tau$是延迟系数。对齐向量$ \left{\mathbf{X}_{i}^{m} \mid i=1,2,…,n}\right. $得到按时间顺序,时间相关的数据矩阵$ \mathbf{P} \in \mathrm{R}^{m \times n}(\tau=1, n=N-m+1) $在相空间中构造,其元素与 x(t) 具有以下关系:
\[P_{(j, k)}=x_{k+(j-1) \tau} \tag{2}\]其中$j \in[1, m], k \in[1, n] .$
然后通过进行短时傅里叶变换 (STFT) 在 TF 域中表示相空间轨迹。 数据矩阵 P 的每一行(具有时间感)由 STFT 分析以提供 TF 表示,如以下等式所示:
\[\mathbf{S}_{j}(k, v)=\sum_{l=-\infty}^{\infty} \mathbf{P}_{j}[l] w[k-l] e^{-i \frac{2\pi}{Z} v l} \tag{3}\]其中k和$v$分别是时间轴和频率轴的位置,Z是STFT中离散频点的个数,w(k)是短时分析窗口。 结果 $\mathbf{S}{j}(k, v)$为复数形式,也可以用两部分表示:幅度 $\mathbf{A}{j}(k, v)$和相位$\mathbf{\theta}_{j}(k, v)$。 幅度部分只是用于 TFM 学习的 TFD,相应的相位部分可以稍后用于 STFT 结果更新。 因此,可以从构建的数据 P 中生成 m 个 TFD,由 m 个大小为 $L \times n$的矩阵表示(L 为频点数,n 为时间点数)。
然后通过将上述 TFD 输入到流形学习算法中,在重建的相空间中计算 TFM。 在这一步中,使用局部切线空间对齐(LTSA)算法 [34] 来计算大小为 L?n 的 d(d 远小于 m)TFM。 有关 TFM 学习过程的更多详细信息,请参阅 [12]。 在本文中,第一个 TFM 签名被用作后续 TF 原子学习的图像。
2.2 TFD 脊分析
对于物理描述,TFD 提供了对 TF 结构的洞察,并给出了非平稳信号的潜在能量分布。 在原始信号的 TFD 中,能量主要分布在 TF 域中的瞬时频率(IF)曲线周围,称为 TFD 脊。 由于 TFD 脊分析是一种 TF 域解调方法,它不仅可以提供 TF 域的瞬时幅度 (IA),还可以给出非线性信号的 IF [35-37]。 基于 TFD 岭,可以推断在 TF 域具有局部最大值的位置代表 TFD 中的 IF。 应用 TFD 脊提取来获取频率集 F,这可以构建有效的 TF 字典并提供匹配路径以更准确地从 TFD 图像中提取瞬态分量。 STFT 脊是一个窗口傅立叶脊。 岭算法根据功率谱或幅度谱的局部最大值计算新的时间序列 IFs,它们通常定义为 STFT 幅度模数达到其局部最大值的位置 (k, v(k))。 TF 点的相应幅度为 IAs。
有几种脊提取算法[36-37]。 与简单的直接最大脊检测不同,Liu [36] 提出了一种成本函数脊检测算法,如方程式。 (4),可以自适应地选择具有动态规划优化的岭。 本研究采用成本算法[36]。 代价算法的主要思想是沿着时间轴寻找一条路径,以最小化在每一点结束的代价函数,并且只关注每一列的局部最大值。 对于大小为 M?N 的 TFD 矩阵,有 (N?1) 个成本函数:
\[C F_{k}=-\alpha[S(k, v)]^{2}+|v(k)-v(k-1)|^{2}, \quad k=2,3, \ldots, N \tag{4}\]确定最后一个山脊上的 N 个点。 参数α是TFD的幅度与频率位置之间的幅度权重。 幅度权重α的默认值为1。当背景噪声过强时,应设置较小的权重α值,以降低幅度的惩罚比例。 通过最小化第k个代价函数CF k 从第k列的候选点{(k, v(k))}中选择第k个脊点(k, v(k))。 这是在确定第(k≤1)个脊点(k≤1,v(k≤1))之后进行的。 因此,脊点是逐步确定的,从 k=2 扫描到k = N。 然而,对于第一点,前两列的所有候选者都应该考虑最小化函数 CF 2 。 通过成本算法,提取中频作为最终结果,这是一个一维时间序列,同时捕获嵌入在给定振动信号中的真实中频信息。 在本文中,从待分析的原始信号的 TFD 中提取的 IF 用于为第 3 节中的图像稀疏分解设置有效路径。
2.3 用于稀疏重建的 OMP
给定希尔伯特空间 $ \mathrm{H}=\mathrm{R}^{L}\left(K^{\text {» }}\right) $ with $ \left|d_{i}\right|=1$,中的集合 $ \mathbf{D}=\left{d_{i}, i=1,2, \ldots, K\right} $,D 称为字典,d i 是字典原子。 由于字典的冗余,di 不再是独立正交的。 对于任何实信号 S ϵ H,S 可以分解或稀疏地表示为 D [15,20] 中的 M 个原子的线性组合:
\[S=\sum_{m=1}^{M} g_{k_{m}} d_{k_{m}} \tag{5}\]其中 $k_m$ 是所选原子的标签,$g_{k_m}$ 是原子 $d_{k_m}$ 的相应系数。 上面的等式是信号的稀疏表示。
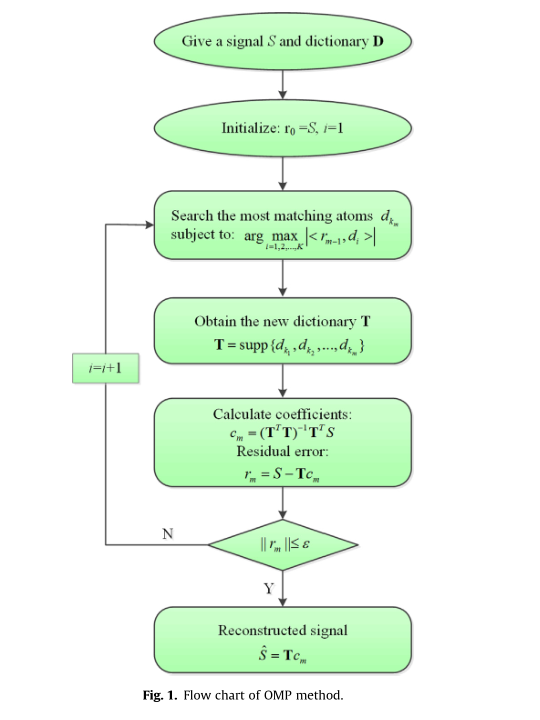
OMP 是对稀疏分解的传统 MP 算法的改进,如图 1 所示。 OMP 的主要思想是使用额外的正交化步骤来提高收敛性。 为了逼近原始信号S,通过OMP方法从过完备字典D中选出一系列最匹配的原子。 该算法是一个迭代过程,通过将信号投影到字典中最接近的匹配原子上,具有最小的近似误差。 在每个匹配过程中,需要注意的是,选择的原子被额外正交化以获得相应的系数。 因此,原始信号 S 被分解为 M 个原子的总和,具有近似信号 $ \hat{S} $ 和残差 $r_M$
对于原始信号 S 的 M 阶近似,重构后的信号可以用下式表示:
\[\hat{S}=\mathbf{T} c_{M} \tag{6}\]其中 T 是基于 OMP 的学习字典,$c_M$ 是相应的系数。 系数可以通过正交化学习字典获得并表示为:
\[\mathbf{T}=\operatorname{supp}\left\{d_{k_{1}}, d_{k_{2}}, \cdots, d_{k_{M}}\right\} \tag{7}\] \[c_{M}=\left(\mathbf{T}^{T} \mathbf{T}\right)^{-1} \mathbf{T}^{T} S \tag{8}\]| 对于迭代 OMP 算法,很容易知道原子数 M 对重建效果至关重要。 太多的原子会给结果带来无用的信息,太少的原子会失去重要的特征。 迭代终止条件通常由所需的精度决定,直到达到终止条件,迭代过程才会终止。 迭代终止条件可以通过残差信号的能量比(记为 R E1 )判断为 ε ε = | > < < R r r / , 0 1 E i 1 2 0 2 。 然而,确定真实信号的有效阈值并不容易。 另一种方法是计算每两个相邻迭代中的能量比变化(用R E2 表示),迭代过程将终止,直到能量比变化连续6次低于预定阈值。 R E2 的迭代终止条件描述为: |
其中 ε 是预定阈值,M 是选定原子的最终数量,r i 和 r i+1 是 OMP 算法的 i 和 i+1 迭代的残差。