1. 土壤放电的本质是辉光放电
单相接地故障的回路电路如图所示。
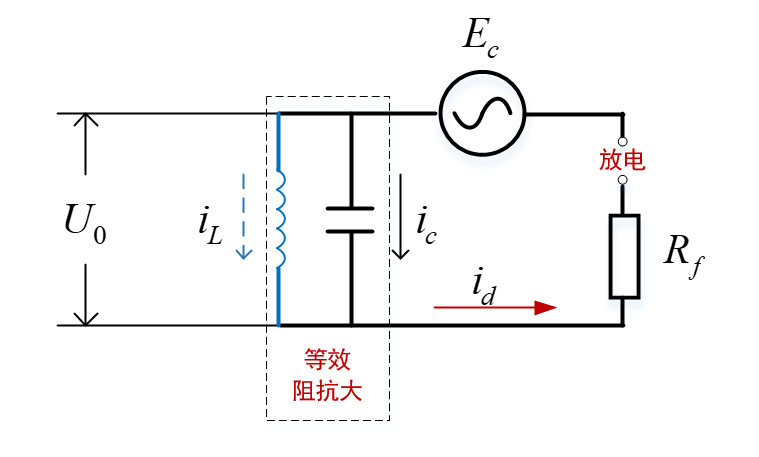
由于回路中的等效阻抗较大,限制了放电电流及功率,单相接地故障放电的本质上是辉光放电。
放电电压、电流波形如图2所示。
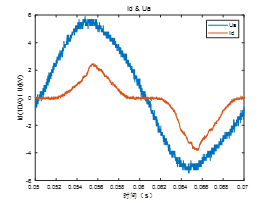
电阻变化波形,零休处的电阻应较大,还未修正的图如图3所示。
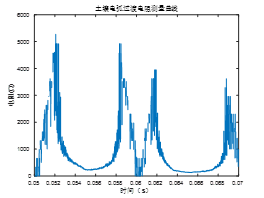
研究土壤接地故障辉光放电,其与高压电气产生的故障电弧,带火花效应的接地极冲击电弧不同之处主要有以下几点:
- 此放电持续时间长,一个完整的放电周期是工频的半个周波,即包括零休时间是10ms,如果去掉零休时间也达到6~7ms。
- 在放电的过程中,电压和电流不断的发生变化,即引起辉光放电的场强经历从小变大又从大变小的过程。
- 接地介质为土壤,土壤是一种导体,但导电性并没有导体那么强,这导致了其有一定的散流电阻,在散流过程中的发热导致其发生热电离,即先导放电,接地点电压越高,先导放电效应越强烈,会向土壤内部深入的更深。
- 又由于土壤本身的导电性,包裹等离子体的未充分电离的土壤能够导电,这使得电场分布与空气放电不同,没有绝对意义上的地,这种先导放电即不能同空气放电一样发展下去,也不会发生主放电。
- 先导放电所形成的等离子体通道,相当于向土壤内部插入一根金属导体,这使得从接地点位置看进去的接地电阻变小了,先导放电形成的等离子体通道在电压最大时刻附近最深,等效电阻最小,而此电阻由于串联在电力系统的零序回路中,会反过来影响接地点的电压,其本质上是一种场路的耦合系统。
所以,配电网发生单相土壤弧光接地故障的整个过程可以描述如下:
单相接地故障的辉光放电主要分为2个阶段,第一阶段是初次接地放电,第二阶段是初次放电电弧熄灭后的放电过程
第一阶段,当配电网架空线或电缆中的一相落到土地表面,此时会在导线和土壤的接触点的位置施加一个电压,这在土壤内部产生了电场,当电场强度达到足够高时,此时的土壤是一种导体,所以场强并不需要很高即可开始放电。土壤作为一种空气,固体和液体的混合介质,其中电场主要集中在空气两端,空气首先被电离,产生流注并迅速发展放热,从而发生先导放电,又由于前面所述原因,该放电并不会发展为主放电,所以维持在先导发展阶段,先导放电产生的等离子体通道向土壤内部延申,其延申长度与接地点施加的初始电压以及后续电压变化相关。当在第一阶段中接地电压逐步降低,由于土壤内的散热特性,使得电场已经维持先导放电所需的热量,电弧熄灭。而此时土壤性质被高温所改变,接地点连接着一种电的绝缘体。
第二阶段,由于土壤性质将接地点所接触的土壤变成了绝缘体,所以当电压再次反向升高时,土壤不会第一时间被击穿,而是当电压升高到一定程度,场强大于此介质的击穿电压时,介质被击穿,重复先导放电,随着电压抬升,先导放电强度增强,而当电压越高最大值逐渐变小时,先导放电逐步减弱,在增强和减弱的过程中,引起土壤等效散流电阻的变化。
由于土壤辉光放电的过程持续时间长,土壤辉光放电过程中,其流注发展的时间很短,这与一个完整的放电过程7~8ms相比,是一个极短的过程,几乎可以忽略,所以,研究土壤弧光接地故障的目的是研究土壤接地电阻如何变化,可以通过研究先导放电的发展着手。
下面是一种借鉴空气先导发展模型而提出的一种基于能量的土壤先导放电发展模型
2. 土壤先导放电发展模型
2.1 能量输入
在先导的发展过程中,总能量$W_t$以不同的形式消耗:热能、电离、辐射等。$W_t$的一部分(动能)将转移到先导通道,使其延长距离$dl_j$。 称 $W_c$ 为动能,记做
\[W_c = \beta W_t \tag{1}\]β 是先导位移所需能量占全部能量的系数。 0 < β ≤ 1 。
在单位时间$dt$内,由于通道发展增加的土壤密度 $ρ$和体积增量 ($\pi r _ { j } ^ { 2 } d l _ { j }$) 的乘积就是增加的等离子体的质量:$m = \rho \pi r _ { j } ^ { 2 } d l _ { j }$(其中$r_j$是分支 j 的半径,气体放电最开始会形成很多枝杈,土壤放电我想先把它简化看成只有1条分支,即j=1)
设通道的半径$r_j$和温度 T 是常数:$r_j = r_0$ 和 $T = T_0$
\[W _ { c } = \frac { 1 } { 2 } \rho \pi r _ { j } ^ { 2 } d l _ { j } v _ { j } ^ { 2 } \tag{2}\]其中 $v_j$是分支 j 的速度。可以将整个等离子体通道从上到下的发展分成若干个区域,因为每个区域的压力不同,所以质量也不同进行迭代。其中第n次迭代符合
\[\sum _ { j = 1 } ^ { n } \frac { 1 } { 2 } ( \rho \pi r _ { j } ^ { 2 } d l _ { j } ) v _ { j } ^ { 2 } = \beta \sum _ { j = 1 } ^ { n } q _ { j } E _ { j } d l _ { j } \tag{3}\]其中 $q_j$和 $E_j$ 分别是分支 j 的电荷和电场。 因此,先导通道的每个位移$dl_j$对应的速度为
\[v _ { j } ^ { 2 } = \frac { 2 \beta } { \pi r _ { j } ^ { 2 } \rho } ( \int i _ { j } d t ) E _ { j } \tag{4}\]2.2 先导发展的平均速度
在文献中描述先导放电电流由许多离散脉冲构成。
令$t_j$ 为脉冲时间$t_{pj}$与停顿时间$t_{0j}$到下一个脉冲的时间之和所对应的时间,即
\[t _ { j } = t _ { p j } + t _ { 0 j } \tag{5}\]和$v_{pj}$和 $v_{0j}$,分别是$t_{pj}$和$t_{0j}$期间的速度。 设 $v_{al}$ 是先导放电发展的平均速度。
\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( v _ { p j } t _ { p j } + v _ { 0 j } t _ { 0 j } ) \tag{6}\]根据公式(4)
\[v _ { p j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { p j } E _ { j } \tag{7}\] \[v _ { 0 j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { 0 j } E _ { j } \tag{8}\]将(7)和(8)代入(6)中,得到
\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } [ ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ] \tag{9}\]$v_{0j}$通常相对于$v_{pj}$可以忽略不计。 $v _ { 0 j }$是在时间$t_{0}$期间先导发展的平均速度。
假设 $r_j$, β, ρ 和 $E_j$ 在整个传播过程中保持不变,发展的平均速度可写作
\[v _ { a l } = ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ) \tag{10}\]当忽略$v_{0j}$时,有
\[v _ { a l } \cong ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{11}\]$E_j$和/或 $q_{pj}$ 越高,先导发展的平均速度就越高。
2.3 等离子体的密度
在高温下,所有气体都可以被认为是完美的。由于先导是高度电离的土壤等离子体 (T ≥ 1000 K) ,还不确定是否可以如此应用气体定律,如果按照完美的气体定律有
\[p V = \frac { m } { M } R T \tag{12}\]其中 p、V、m、R、T 和 M 分别是压力、体积、通道质量、理想气体常数、温度和通道的摩尔质量。
由于密度 ρ 等于 m/V,可以得到
\[\rho = \frac { M } { R } \frac { p } { T } \tag{13}\]因此式(13)可以写为
\[\rho ( kg m ^ { - 3 } ) = \frac { k } { T ( K ) R } \tag{14}\]其中,$k = Mp$
气体等离子体的压力是恒定的,所以k也是定值,但土壤由于深度不同,由于重力的影响,此时的k应该是变化的,如何变化还需要进一步确定。
2.4 先导发展头部电场计算
对每一步先导发展来说,场强 $E_j$ 是必不可少的。该场强$E_j$ 与沿通道分布的总电荷有关。 Szpor (1971) 提出了这一假设,可以使用双曲线近似来估计:
\[E _ { j } = \frac { 2 U _ { j } } { R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } \tag{15}\]$L_z$和 D 分别是前导轴向长度和间隙长度,$U_j = U − \Delta U_j$是先导尖端上的电压(其中 U 是电极上施加的电压,$\Delta U_j$是沿通道的电压降)和 $R_e$ 等效电极的半径。
$R_e$ 可以表示为等离子长度的线性关系
\[R _ { e } = \alpha L_z \tag{16}\]按照试验后的土壤挖掘结果,$\alpha \cong 1/10$
2.5 先导放电的平均速度计算
联立式 (11)、(14) 和 (15)
\[v _ { a l } = ( \frac { 4 \beta T _ { 0 } U _ { j } R } { \pi r _ { 0 } ^ { 2 } k R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } ) ^ { 1 / 2 } \times ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{19}\]先导的速度取决于先导尖端 $U_j$ 处的电压、其轴向长度 $L_z$ 和其他物理参数, 还有参数$\beta$。
3. 总结
通过以上计算,就可以按照发展步长计算出先导放电的等离子体通道深入土壤内的长度,该长度应该是和土壤的等效电阻挂钩的,这种长度和等效电阻的关系还需要进一步进行确定。
目前推导是一种可能的计算方法,还没进行更深入的研究,其中的一些参数的获取还需要做进一步研究。