1. 电弧故障定位：非线性时变故障模型和频域参数估计方法

1. Arc fault location: A nonlinear time varying fault model and frequency domain parameter estimation approach

1.1 摘要

本文提出了一种非线性电弧放电故障定位的频域公式。提出的故障定位公式将故障起始电压和电流之后的第一个周期用作输入数据。该公式基于电路分析和参数估计方法。为考虑非线性电弧故障的主要特征，提出并使用了嵌入非线性模型中的时变电阻。该公式是针对使用相分量的最常见单线接地故障而开发的。研究分析了故障起始角，时变串联电阻，源阻抗，潮流，采样频率等因素的影响。通过计算机仿真和从巴西南部能源公司获得的真实数据，成功测试了这种新方法。拟议的方法是作为专用软件开发的，CEEE-GT目前正在使用。

1.2 引言

传输线用于长距离传输电力，并且自然暴露于恶劣的天气条件下，尤其是架空线。这样的条件非常有利于故障的发生。统计数据显示，架空线路上70％到90％的故障是非永久性（或瞬态）的，并且存在电弧。这些故障中有90％以上是单线接地的[1,2]。电弧是这些故障的主要特征，并且是通电的导体与地面或接地物体之间接触不良的结果[3]。

在过去的几十年中，为提高传输系统的可靠性，安全性和电能质量做出了巨大的努力。为此，已经提出并实施了保护方案和故障检测/定位技术。准确的故障定位算法可通过减少故障引起的中断时间来提高电力系统的可靠性，安全性和电能质量[4]。在这方面，基于阻抗的故障定位方法由于其简单性和较低的实施成本而被广泛使用[5]。

基于基于阻抗的电力系统故障定位方法已经提出并发表了几篇著作[6,7]。然而，相对较不完善的方法是使用基于频域方法的基于阻抗的非线性电弧故障（NAF）技术，如高阻抗故障（HIF / NHIF）[2,8-10]。在[2,8,9]中，发展了电弧故障识别和故障距离估计。根据估算的电弧电压幅度，可以确定故障是永久故障还是瞬态故障。然而，在这些工作中并未考虑几种NAF特性（随时间变化的行为）。 [10]中提出的技术使用了来自两个端子的零序电流（适用于理想的换位线）和源阻抗数据，用于线对地NHIF公式。但是，在非换位线的情况下，不适合采用对称分量法。此外，源阻抗是动态的，难以实时估计。

NAF表现出一些不常见的故障特征[11]，当前的基于阻抗的最新配方并未考虑到这些特征，从而阻碍了它们的性能。在制定问题时必须解决和考虑此类故障特征。从这个意义上讲，在基于阻抗的公式中必须考虑时变，非对称和非线性特性[12]。

本文提出了一种在频域和相位分量中考虑NAF特性的基于阻抗的故障定位公式。本文提出的方法考虑基于最小二乘法（LSM）和在两个线路终端获得的同步相量测量的参数估计方法。仍然，所提出的方法仅将故障起始电压和电流之后的第一个周期用作输入数据。

通过考虑三个主要的NAF特性：时变，非对称和非线性特性，所提出的公式为基于阻抗的最新故障定位公式做出了明确的贡献。仍然可以将所提出的方法用于永久性和非永久性故障的故障定位。最后，正如目前在CEEE-GT上使用的那样，该配方能够进行预防性维护，因为绝大多数非永久性故障会演变成永久性故障。

本文的其余部分安排如下。 “ NAF建模”部分介绍了具有随时间变化的串联电阻的NAF建模。 “建议的NAF公式”部分介绍了建议的故障位置公式。 “结果和算法评估”部分介绍了包含模拟和现实数据的案例研究。结论在“结论”部分中给出。

1.3 Modeling a NAF

Nonlinear arcing faults(NAF)

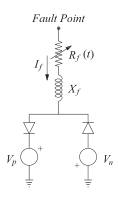
作为HIF的NAF是一种特殊的故障类别，例如，当通电的导体与高电阻表面进行电接触时会出现。这些故障的主要特征是：波形非常不稳定的故障电流，电弧[3]，累积，肩峰，非线性和不对称[11]。本文使用的NAF模型基于[12]的工作，其中电弧是通过两个直流电源Vp和Vn建模的，两个直流电源通过两个二极管反并联连接。二次和三次谐波电流表示为DV = Vn·Vp和tanh = Xf / R的函数。在这项工作中，建议对[12]提出的模型进行一些修改。该修改包括将恒定的R值替换为随时间变化的串联电阻Rf（t）。这样可以正确表示积聚和肩部特征。图1（a）描绘了使用的NAF，图1（b）显示了典型故障电流，其中非线性模型中嵌入了随时间变化的串联电阻。

图1（a）所示的NAF模型的参数Vp，Vn，Xf和Rf（t）取决于断层接触面的特征，例如孔隙率，湿度，密度和组成[13]。 ]。在这项工作中，可以使用具有不同接触表面的模拟NAF来访问拟议的配方性能，例如：本地土壤，树木，沙子，沥青和草。例如，图2给出了每种情况下此类故障电流行为的图示。

Rf（t）的时变行为可以通过多项式函数来近似：

\[R _ { f } ( t ) = \left\{ \begin{array} { l } { a _ { n } t ^ { n } + a _ { n - 1 } t ^ { n - 1 } + \cdots + a _ { 1 } t + a _ { 0 } , \text { for } t _ { fi } \leq t \leq t _ { ss } } \\ { a _ { 0 } , \text { for } t > t _ { ss } } \end{array} \right. \tag{1}\]

其中tfi是故障开始的瞬间，tss是Rf（t）达到稳态的瞬间。

此过程首先在[13]中提出，其中通过多个接触面的现场测试获得了HIF建模过程。使用在巴西南部230 kV输电线路上发生的实际断层情况的同步测量，估算了当地土壤和树木上的NAF的Rf（t）值。 Rf（t）的其他值是[13]中给出的修改后的版本。与前两种情况相比，进行这些修改是为了获得堆积现象的相似持续时间。调整Vp，Vn，Xf，以近似当地土壤曲线的行为。仿真中使用的所有值在附录表1中列出。

2. EMTP中两个串联时变电阻的配电系统高阻抗故障建模方法

2. A Modeling Method of a High Impedance Fault in a Distribution System Using Two Series Time-Varying Resistances in EMTP

2.1 摘要

用于检测高阻抗故障（HIF）的更可靠的算法需要在中继点而不是发生HIF时出现故障的分支的电压和电流数据。因此，HIF的精确建模方法对于开发可靠的检测算法至关重要。数据应包含HIF的复杂特征，例如堆积和肩部以及非线性和不对称性。本文提出了一种上述HIF特性的建模方法。在韩国电力公司（KEPCO）进行的22.9（kV）配电系统的实验数据中，本文选择了具有上述所有特征的实验数据。建模中采用了由EMTP中的控制系统瞬态分析（TACS）控制的两个串联时变电阻（TVRS）。一个TVR用于在HIF之后稳定状态下一个周期的电压-电流特性的非线性和不对称性，然后另一个TVR用于在HIF之后的瞬态状态下的波形建立和承受。建模结果与实验数据的比较显示出紧密的对应关系。利用改进的HIF模型，可以在各种负载条件和故障条件（例如故障距离和起始角度）的情况下获得中继点的电压和电流。

1. 引言

当HIF发生在配电系统中时，故障电流的大小不会比负载电流大。此外，它还具有复杂的特性，因此，据报道，用于HIF的继电器仅能检测到其中的50-60’？ZO。 HIF具有复杂的特征，例如堆积，肩峰，非线性和不对称。 [1,2]

应该基于包含负载条件和HIF特性的数据，开发出更可靠的HIF检测算法。为了获得这些数据，有必要开发一种具有上述HIF特性的建模方法。

已经提出了一些HIF的建模方法。在[3]中提出了使用二极管的建模方法，在[4,5]中将HIF建模为电压源。尽管这些方法很好地表示了HIF的非线性特性，但是当表示其他特性（例如堆积和肩部）时，就会出现困难。

本文提出了一种用于表示HIF的上述特征的建模方法。在由KEPCO进行的有关配电系统的各种实验数据中，本文选择了显示所有上述特征的实验数据。所提出的方法在EMTP中采用了由TACS控制的两个系列TVRS。一个TVR用于故障后稳态下一个周期内电压-电流特性的非线性和不对称性，然后，另一个TVR用于根据HIF后瞬态下的波形来表示累积和肩峰特性。在HIF之后的任何瞬间，两个TVRS的总和对应于故障电阻。根据开发的HIF模型，可以通过各种负载条件和故障条件（例如，使用EMTP的故障距离和起始角度）获得继电器点的电压和电流。

2. HIF故障建模

A. 高阻故障的特征

KEPCO在22,9（kV）配电系统上进行了HIF实验。实验总数为32，采样频率为10 kHz。但是，实验数据是在故障分支而不是中继点处测量的，这意味着在测量数据中不包含有关载荷的信息。

其中，图1显示了碎石上HIF实验数据的电流波形。在图1中，电流在大约15个周期内达到最大值，这意味着积聚。但是要注意的是，在这种情况下肩部几乎未示出。

图2表示在鲁棒卵石上进行HIF实验的电流波形。此图中的电流具有肩峰和积聚，在HIF后4’〜，12（〜和24’hh周期左右，积聚停止3-4个周期，电流在约35个周期内增长到最大值，达到稳态需要的时间比图1多，这是由于肩部引起的，如图2所示，堆积和肩部仅在HIF之后的稳态之前存在，而诸如非线性和不对称性的特征则在之前和之后出现。例如，图3例示了图2的HIF之后第20和40个周期的电流，这两个电流都具有非线性和不对称的特性，

B. HIF模型

由于具有上述所有特征，因此本文选择进行建模。本文旨在代表HIF的各种特征，即堆积和肩部以及非线性和不对称性。在K.EPCO进行的HIF实验结果中，由于具有上述所有特征，因此本文选择了图2的稳固卵石进行实验。

所提出的方法采用两个串联的TVRS来表示这些特性。

如图2所示，在HIF之后的稳态中仅存在非线性和不对称性，而堆积和肩部则不存在。此外，对于每个稳态，非线性和不对称性的特征在每个周期都是相似的。因此，可以在稳态下从一个周期的当前数据对非线性和不对称性进行建模。时变电阻R（t）用于表示非线性和不对称性，并且在每个周期的稳态下具有相同的特性。

另一方面，如图2所示，仅在稳态之前存在诸如堆积和肩峰之类的特性，并且故障电流在每个周期的每个周期具有不同的大小。因此，如果RI（t）也用于模型的建立和肩部，应在瞬态下的每个周期更改它。因此，在建模堆积和肩部方面会出现实际困难。

如上所述，在HIF之后，堆积和肩部在稳态下消失，而在HIF之后的每个循环中都存在非线性和不对称性。基于这个事实，另一个时变电阻R2（t）用于考虑累积和承受。所提出的方法将HIF建模为如图4所示的两个串联TVRS的总和，并且将HIF之后的时间t的总抗电阻R（t）给出为

\[R ( t ) = R _ { 1 } ( t ) + R _ { 2 } ( t ) \tag{1}\]

在（1）中，R，（t）具有周期性，这意味着RI（t）等于R，（t + T）； T是周期。另一方面，R2（t）在HIF的开始处具有非常大的值，然后其值在过渡状态下单调减小，在HIF之后的稳态下变为零。在本文中，由于在HIF之后没有在稳态下的堆积和肩峰，所以从稳态期间的电压和电流数据获得RI（t），然后从瞬态状态的数据确定R2（t）。

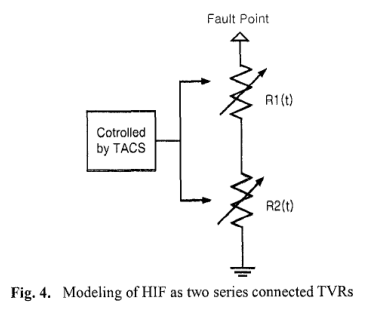
图5显示了图2中40r〜周期的电压-电流特性曲线，RI（t）由时间t的电压与电流之比定义，并从稳态下一个周期的电压和电流获得在HIF之后。为了将电压-电流曲线精确地实现到EMTP的TACS中，图5的曲线上的许多点是必需的，这很繁琐。因此，本文采用图6代替图5的线性化电压-电流特性曲线。在1’r和3” {象限上分别选择了七个点进行线性化。此外，一个电压值映射到两个电流值。为了区分两个值，使用了电压的导数。电压的正导数对应于1’〜象限的上线，而负导数对应于下线。

如果从故障分支带来的电压在Vfl <v（t）<Vfl + 1的范围内，则通过

\[i ( t ) = i _ { n } + \frac { i _ { n + 1 } - i _ { n } } { v _ { n + 1 } - v _ { n } } \times ( v ( t ) - v _ { n } ) \tag{2}\]

然后RI（t）估计为

\[R _ { 1 } ( t ) = \frac { v ( t ) } { i ( t ) } = \frac { v ( t ) } { i _ { n } + \frac { i _ { n + 1 } - i _ { n } } { v _ { n + 1 } - v _ { n } } \times ( v ( t ) - v _ { n } ) } \tag{3}\]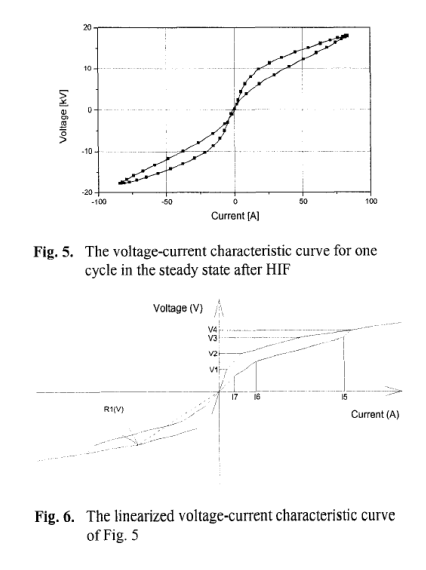

在分配线的末端进行了图5的HIF实验。因此，当在变电站附近的某个点模拟HIF时，故障分支处的电压v（t）会大于实验峰值电压V；。在本文中，如果v（t）大于V；，将RI（t）的斜率设置为前一个斜率，如图6所示。

3. 高阻接地故障，从实验到模型

3. High Impedance Faults: From Field Tests to Modeling

dos Santos W C, de Souza B A, Brito N S D, et al. High impedance faults: From field tests to modeling[J]. Journal of Control, Automation and Electrical Systems, 2013, 24(6): 885-896.

3.1 摘要

高阻抗故障（HIF）十分严重，并且干扰了配电系统的故障，因为主电源系统保护设备通常由于故障电流水平低而无法准确诊断它们。本文介绍了现场实验和HIF建模的详细信息。对HIF模型进行了文献综述，并建议使用文献中已知的模型进行一些调整。使用该模型，可以基于在不同接触表面获得的实际记录，获得一组模拟记录，这些记录代表了在大多数HIF中发现的最重要特征。

3.2 引言

从概念上讲，配电系统包括在其特许经营区域内属于配电商的配电线路和电气设备，包括按合同提供给配电商但不属于基本电网的其他配电和输电设施（ANEEL 2011）。根据《消费者保护法》（巴西，1990年）第22条，要求分销商提供适当，高效和安全的服务，并且基本服务必须是连续的。在这些参数中，服务的连续性被认为是至关重要的，因为它影响人们的日常生活，并通过损害对消费者的基本服务而造成重大破坏。

连续性是指用户可利用的电力的程度。理想的情况是不要中断电力供应；为此，应尽量减少这种情况，并及时告知消费者，以防止因能源不足而造成的可能损失。但是，由于缺陷以及网络预防性维护服务的执行，消费者会受到能源供应中断的影响。其中，最令人担忧的是由于电气，机械或故障问题而导致组件的非计划停机的故障。热性质，是由系统始终受到的不利条件引起的。在实践中，故障是由电缆线吸附设备故障引起的。通过定期维护设备可以避免某些故障；但是，大多数故障是由自然现象引起的，例如闪电，雨水，强风等。

在配电系统中，特殊的一类称为高阻抗故障（HIF）的故障通常会引起关注，主要是天线配电网。通常，在具有高电阻表面（例如树木，道路）的主网络电路的通电或故障的导体接触时，会发生HIF。结果，HIF可能会使人身遭受电击的危险，从而损害系统设备的完整性，严重损害性能，并导致保护系统启动后大量用户没有电源。由于主要是放射状的拓扑结构，带有大面积延伸的馈线和跨越较长的无人区，这种问题在农村配电网中更加严重。

由HIF引起的问题主要是由于产生的电流水平，不足以使常规保护熔断器和继电器的运行变得敏感。由于此特性，由于插入/移除负载或电容器组切换，HIF经常会与网络中的振荡瞬变相混淆。结果，缺陷可能会持续存在。

在巴西电力部门的当前情况下，特许公司通常通过消费者投诉来检测HIF发生的方法。此过程可能很耗时，并且取决于用户提出投诉之前的延迟，然后取决于将此信息传递给维护人员的速度。为了减少由HIF引起的停电时间和运营成本，公司已经投资开发了自动恢复电源的解决方案。为此，首先需要对事件进行详细描述，即进行诊断。在电力系统中，这转化为事件的检测，分类和定位的实施阶段。在当前的软硬件状态中，这是一个很重要的话题，并且越来越重要（Chan and Yibin 1998； Lazkano etal.2000； Moreto2005； Yangetal.2007； Souzaetal.2011）。

通常，诊断算法的开发需要使用计算机模拟的标准来构建，该标准代表了各种故障情况（Souza等，2005）。这种组合通常称为数据库。在HIF的特定情况下，提供的诊断的质量主要取决于用于表示现象的模型，因此取决于数据库的质量。模型越接近实际现象的特征，基于这些特征的诊断算法将越可靠。

在评估现有技术水平时，已经发现在HIF的构建模型方面有许多工作要做，因为迄今为止提出的模型未能完全代表这一现象（YuandKhan1994; YibinandChan1996; Nakagomi 2006; Santos 2011）。从这个意义上讲，本文提出了对HIF模型和使用该模型的文献综述，该模型结合了现有模型的特征和一些创新功能。最后，获得了代表在最HIF中发现的最重要特征的模型。该模型的实现是在ATP（鲁汶EMTP中心1987）上进行的，使用的是语言MODELS。

3.3 高阻模型综述

3.3.1 高阻模型的主要特征

HIF的主要特征是故障电流的幅值低，在大多数情况下，该幅值与由其他现象（例如负载通电/断电和电容器组切换）产生的电流大小相同（Wester 1998）。

在HIF形成过程中观察到其他重要特征。根据Nakagomi（2006）的说法，当一个导体破裂时，当它接触到一个高电阻的表面时，它并不会一开始就确定电接触。但是，随着空气中的自由电子被导体和表面之间形成的电场加速，这种接触会加剧。当达到给定的动能阈值时，空气中的中性分子被电离，释放出新的自由电子。然后，电子与中性分子连续碰撞的过程在短时间内启动。这个过程称为雪崩。因此，空气开始具有导体的作用，从而产生电弧。在电弧形成过程中，经常发生闪烁（电介质瞬时中断的快速序列）。

电弧在专业文献中得到了广泛的研究。然而，大多数研究涉及电力传输线故障产生的电弧，这些电弧通常具有以下特征：米级长度，数千安培范围内的初始电流，主要是感应阻抗和均匀的接触表面。在HIF的特殊情况下，弧长为：约几厘米的长度，小于百安培的电流，主要是电阻性阻抗以及不均匀的接触面（由不同电阻率的层表示）。因此，在HIF的情况下，可能不会充分发生金属汽化以保持电弧稳定，这可能导致故障电流不连续（Jeerings和Linders 1989）。

电击HIF的存在可能导致电流波形出现某些特殊情况，例如半波之间的不对称，波形失真，电流的逐渐增加（累积），振幅的恒定力矩（肩部）以及间歇性（图1）。 toEmanuel etal。（1990年），来自HIF的故障电流具有不对称特性，正半波的幅度大于负半波。根据作者的说法，此特征不取决于电极的形状或电极制造中使用的材料。影响最大的因素是表面接触的孔隙率和湿度。特别地，不对称性可归因于二氧化硅，二氧化硅是通常存在于接触表面中的物质。加热时，二氧化硅形成一种吸收电子的阴极斑点，当导体承受正电压时，会引起较小的电压降。

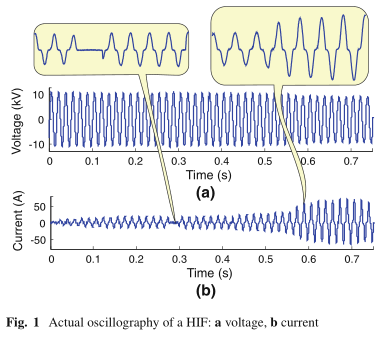
仍然根据伊曼纽尔等人。（1990年），当电弧开始时，土壤中电场的分布发生了很大的变化，导致导体和接触表面之间的电场急剧上升。诸如热离子发射和高场梯度等因素以及土壤导电层随时间变深的事实使得电弧进一步进入土壤。结果，通过接触表面的电流传导最终产生了辉石，该辉石是由于土壤中存在的二氧化硅玻璃化而形成的管状岩石结构。随着电弧渗透到接触表面中，其周围的区域开始失去水分，迫使其熄灭。从此阶段开始，另一区域的土壤水分可能扩散，导致电弧重新点燃或与接地导体的另一个接触点；以及可能会引发新电弧的形成。此过程发生在故障的初始阶段，称为间歇性故障，这会导致在故障点出现电压和电流的高频分量。

在HIF的示波器记录中，通常会观察到故障电流包络线的增长。这种行为被称为堆积，是由于电缆的物理适应性导致的现象，即电缆完全沉入土壤中时，确定了HIF的最后接触电阻。通常，这种生长会停止几个周期，这就是所谓的肩膀的特征。

所有这些特性都是系统的几何，空间，环境和电气条件的函数（Kaufmann和Page 1960）。结果，HIF中所涉及的电量的行为具有很强的随机性，因此需要对现象进行详细研究才能建立现实的模型。

3.3.2 高阻电弧模型综述

由于难以获得真实的示波器数据，因此HIF的研究并非易事。因此，使用模型是诊断此类事件的主要步骤。本节介绍了HIF的主要模型。

模型1： Sharaf and Wang (2003)

模型由具有恒定故障电感L f的可变故障电阻R f串联而成（图2）。

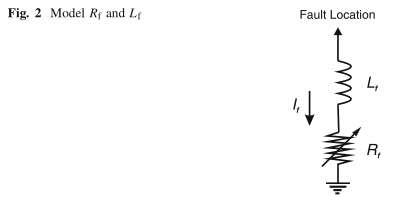
R f的值计算如下：

\[R _ { f } = R _ { f 0 } \cdot ( 1 + \alpha \cdot ( \frac { i _ { f } } { i _ { f 0 } } ) ^ { \beta } ) \tag{1}\]

其中R f0是初始故障电阻，α和β是预定参数； i f和i f0分别是当前和初始故障电流。该模型仅模拟电流的非线性和不对称特性。

模型2：Emanuel et al. (1990)

由恒定电感串联组成的模型，由两个反并联连接的二极管组成，每个二极管与一个连续电压源串联（图3）。

在正半周期内，故障电流通过平均软的电压源VP循环，而在负半周期内，VN的电源循环。由于故障电流的正半周大于负号，因此使用了VN> VP。谐波含量的发生由电源之间的差值控制（$\Delta V = V_N - V_P$）电抗XL和电阻R的比值（$tanθ= XL / R$）。

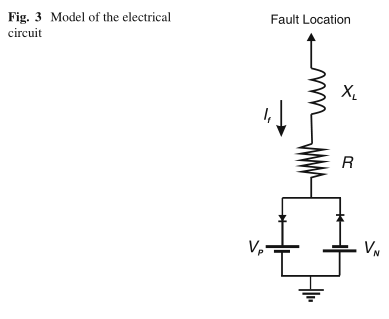
该模型仅模拟电流的非线性和不对称特性。

模型3：Nam et al. (2001)

模型由两个串联的电阻组成，两个电阻随时间变化，并由ATP的控制系统瞬态分析（TACS）程序控制（图4）。

电阻R 1模拟HIF的非线性和不对称特性，在过渡状态和永久状态下起作用。通过使用一个周期的电压-电流曲线来计算其值，在该曲线中，不存在与后续周期相关的幅度的明显变化。因此，可以认为在选定的周期中没有堆积现象和肩峰现象的影响，这允许在故障点处的电压和相应的电流之间进行分配，从而产生模拟不对称和非线性特性的电阻 HIF电流的。

电阻R 2模拟堆积（故障电流升高的周期）和肩部（故障电流在开始上升之前保持恒定的周期）的现象。通过将电压的半个周期的绝对最大值除以电流的绝对值来计算其值。由于稳态系统操作仅受R 1的影响，因此从预先获得的曲线中减去其稳定后的值（R 1），并且获得了与堆积和肩部特征有关的行为（R 2）。最后，进行回归分析，以通过方程作为时间的函数来近似R 2的点。因此，该模型模拟了非线性，电流不对称，累积和肩峰的特征。

3.4 高阻电弧模型建议

基于文献中讨论的模型，本文建议的HIF模型如图5所示。

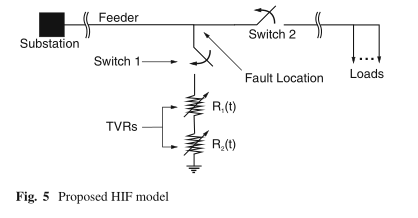
所提出的模型模拟了HIF的主要特征，例如非线性，不对称，堆积和肩峰。该模型执行如下：

TACS控制的串联两次时变电阻（TVR），例如Nam等人提出的。（2001）。电阻R 1：模拟非线性和不对称的特性。电阻R 2：模拟堆积和肩部现象。
在可变故障电阻模型中添加了两个时间控制的开关：开关1：将电阻连接到故障点并启动故障。开关2：连接到故障点的下游，模拟导体的断开。

HIF的某些诊断方法在其算法中考虑了电导体的断裂（Malagodi 1997）。此故障会导致故障点下游的电压明显失衡。插入开关2可以考虑馈线末端的这种现象。

图6显示了HIF的模拟记录，并在故障点的下游点采集了数据。由于在图6a中没有开关2模拟导体的断开，因此在相之间的电压没有很大的不平衡。在图6b中没有发生同样的情况，图6b中考虑了导体与土壤接触时的断裂。

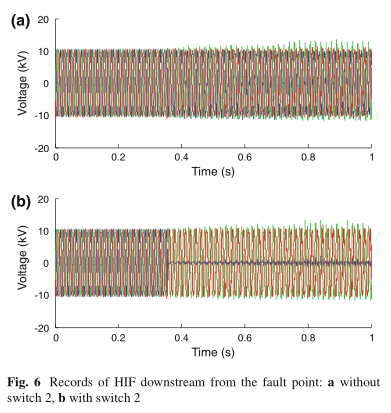
考虑到干燥和潮湿的表面，对7种类型的表面（草，鹅卵石，砾石，沥青，沙子，局部土壤和灌木丛）进行电气测试，可以完成对模型软件参数的调整。在测试中获得的示波器中，每种土壤中只有一种在所讨论的接触面模型的参数化中被滥用。该模型的有效作用是通过使用实际数据来考虑其参数中的不同接触面。

Nam等人计算出与故障间隔电压相对应的电流。（2001）：

\[i ( t ) = \left\{ \begin{array} { c l } { i _ { n } + \frac { i _ { n + 1 } - i _ { n } } { v _ { n + 1 } - v _ { n } } \times \Delta v , } & { \text { se } v _ { n } < v ( t ) < v _ { n + 1 } } \\ { i _ { n } , } & { \text { se } v ( t ) = v _ { n } } \end{array} \right. \tag{2}\]

其中v（t）是故障点馈线中的电压; $\Delta v = v（t）− v_n$； $v_n$和$i_n$分别是样本n中特性曲线的电压和电流。

由于特性曲线对每个对应的电压值显示两个电流值，因此使用了一种技巧来正确选择要在等式中使用的值。（2）：将总曲线分为两部分，一部分对应于变量的增长（上升曲线），另一部分对应于变量的下降（下降曲线）。

语言MODELS中实现的算法通过故障施加点处的电压导数的演算来区分正确的曲线。如果导数为正，则所选曲线将为上升曲线。否则，它将是下降曲线。

此外，根据图7，每种土壤在曲线vxi的特性和最大电流振幅的值上都有差异。这些差异是接触面成分的特定特性（例如孔隙率，湿度和密度）的函数。由于可以获得与现实最接近的模拟HIF模式集，因此这一考虑至关重要。

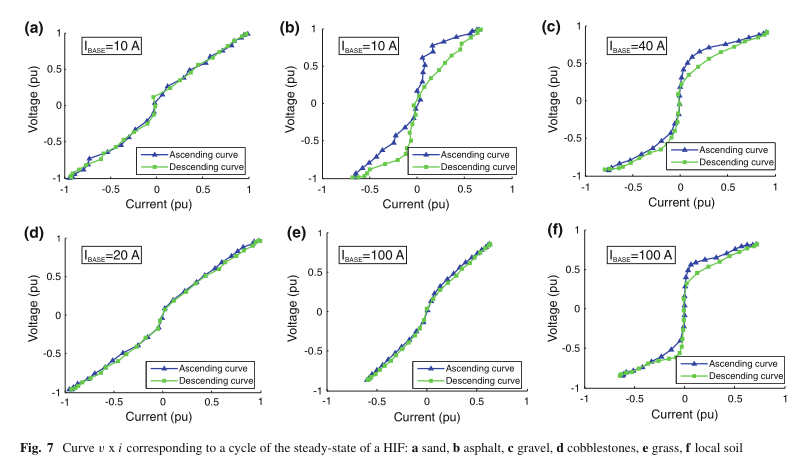
按照Nam等人提出的方法。（2001），电阻R 1通过以下方式估算：

\[R _ { 1 } ( t ) = \frac { v ( t ) } { i ( t ) } = \frac { v ( t ) } { i _ { n } + \frac { i _ { n + 1 } - i _ { n } } { v _ { n + 1 } - v _ { n } } \times ( v ( t ) - v _ { n } ) } \tag{3}\]

为了估计电阻R 2（以鹅卵石表面为例），完成了图8所示的过程。

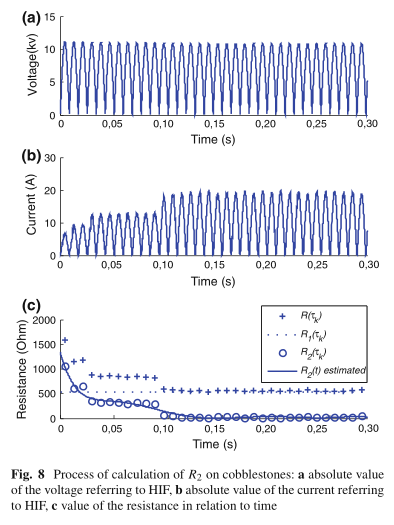
HIF中的电流主要具有电阻特性。因此，将电流与电压同相考虑（Nam等人，2001年）。因此，总电阻（R = R 1 + R 2）可以通过将v的值除以i来直接获得。

由于累积和肩峰现象与故障电流幅值的变化有关，因此仅考虑电压和电流的绝对最大值即可计算出电阻R 2。为此，τk被认为是第k个半周期中电压和电流达到最大值的瞬间。

假设故障电流的非线性和不对称特性在所有周期中都相同，则可以将R 1（τk）视为在所有HIF持续时间内近似恒定。通过这样做，可以通过从R（τk）减去R 1（τk）来获得电阻R 2（τk）。

为了保证在HIF期间仅电阻R 1具有影响，假定在该时段中电阻R 2的值近似为零。

最后，根据等式，通过多项式回归来近似电阻R 2。（4）：

\[R _ { 2 } ( t ) = \left\{ \begin{array} { c c } { a _ { n } \cdot t ^ { n } + a _ { n - 1 } \cdot t ^ { n - 1 } + \dots + a _ { 1 } \cdot t + a _ { 0 } , } & { \text { set } < \Delta t } \\ { 10 ^ { - 5 } , } & { \text { se } t \geq \Delta t } \end{array} \right. \tag{4}\]

其中n是函数度，系数a k是通过methodfleastsquares确定的，而t是HIF电流的增长周期。

为了使由$R_2（t）$的方程式提供的近似值与测量点$R_2（t）$相比较，选择确定系数$R^2$。该系数通常在实际情况下使用，例如在这种情况下显示的系数，因为该系数比对电阻图进行的可能的目视检查更为可靠的分析（Mathworks，Inc. 2007）。

确定系数$R^2$是对表示一组确定的数据的模型进行调整以适应一组参数的能力的度量（Lira2008）。它的定义为在计算和测量信号（SSE）的平方误差之和与总和之间减去1（一个）。根据以下方程式（The Mathworks，Inc. 2007; Spiegel et al。2001）相对于被测信号（SST）平均值的平方误差的平均值：

\[SSE = \sum _ { j = 1 } ^ { m } [ r _ { med } ( j ) - r _ { est } ( j ) ] ^ { 2 } \tag{5}\] \[SST = \sum _ { j = 1 } ^ { m } [ r _ { [ \operatorname { med } } ( j ) - \overline { r } _ { med } ] ^ { 2 } \tag{6}\] \[R ^ { 2 } = 1 - \frac { SSE } { SST } \tag{7}\]

其中$r_{med}（j）$和$r_{est}（j）$分别是电阻的测量值和估计值； m是样本数； $\overline { r } _ { med }$是测得的电阻的平均值。

为了获得良好的调整，必须使SSE低，即，估计值接近于测量值。在这种情况下，确定系数将接近1（一）（Lira 2008）。

表1列出了多项式函数的参数（直到八度才进行评估），这些参数应估算每种土壤的测得电阻值。除了参数之外，示出确定系数R 2以使得能够验证所执行的调整的质量。从每种类型的接触表面的多项式函数获得的曲线如图9所示。

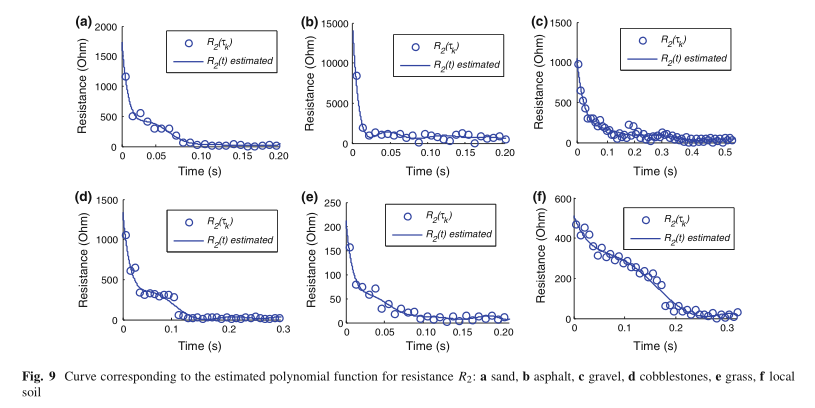
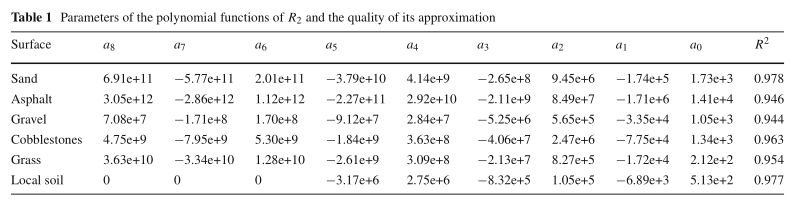
在测试和建模阶段，由于操作问题，并非所有理想的接触面都得到了解决。理想的实验是考虑该区域可能发生HIF的土壤的最大数量。但是，在其他HIF情况下，建议的方法可以完美地用于确定模型的参数。

对六种类型的表面执行了所有建模过程，这些表面具有从现场测试获得的实际数据（草，鹅卵石，沥青，沙子，砾石和局部土壤）。

目前，这还没有建立起HIF的检测方法，这主要是因为该故障对受保护设备监控的电压和电流的影响很小（Costa等人，2011年）。与电气系统中发生的现象相比，仿真模型的特征范围越大，基于这些仿真的诊断算法的可靠性就越高。此处介绍的模型检查了HIF的主要特征，在处理与检测和定位此类故障的未来研究中显示出巨大的潜力。