Modeling secondary arc based on identification of arc parameters from staged fault test records

PRIKLER L, KIZILCAY M, BAN G, et al. Modeling secondary arc based on identification of arc parameters from staged fault test records [J]. Int J Elec Power, 2003, 25(8): 581-9.

结果表明，除了故障相和声相之间的电容和电感耦合外，电弧参数的随机变化会显着影响电弧消光时间。电弧模型的参数已经从在双回路，未补偿的400kV互连线路上进行的分级故障测试记录中提取。仿真结果证明了输电线路的分布特性和电弧间歇区域电弧电阻的非线性特性的重要性。电弧电流由该间隔中的波浪过程确定。结果，表征第二次电弧放电周期的连续电流之后是更高幅度的单个电流脉冲。第二周期的高能量重新点火可以将电弧放电过程推回到连续状态，这使自消光时间倍增。

而本文采用的电弧模型依然是控制论模型。

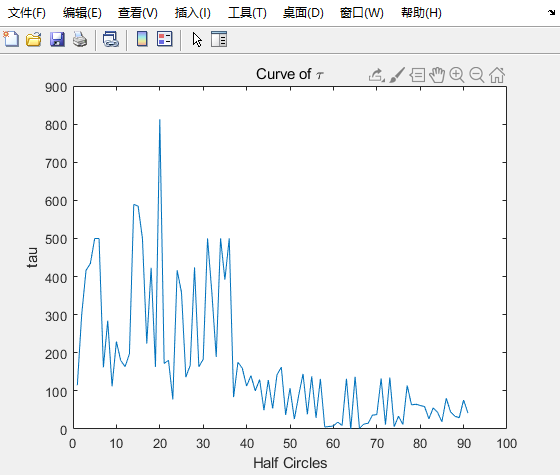
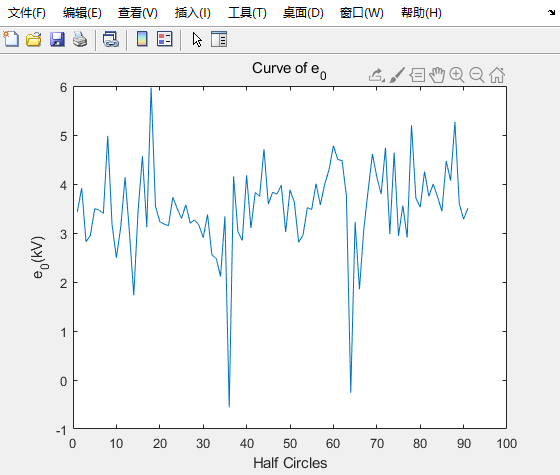
\[u _ { 0 } = \frac { \int _ { t _ { 1 } } ^ { t _ { 2 } } | i _ { \operatorname { arc } } | d t } { \int _ { t _ { 1 } } ^ { t _ { 2 } } g d t } \tag{1}\] \[\tau = \frac { \frac { 1 } { u _ { 0 } } \int _ { t _ { 1 } } ^ { t _ { 3 } } | i _ { arc } | d t - \int _ { t _ { 1 } } ^ { t _ { 3 } } g d t } { g ( t _ { 3 } ) - g ( t _ { 1 } ) } \tag{2}\]

程序

按照说明，我们需要从t1积分到t2，其中$g ( t _ { 1 } ) = g ( t _ { 2 } )$

那么按照曲线我们从50点积分到180点。

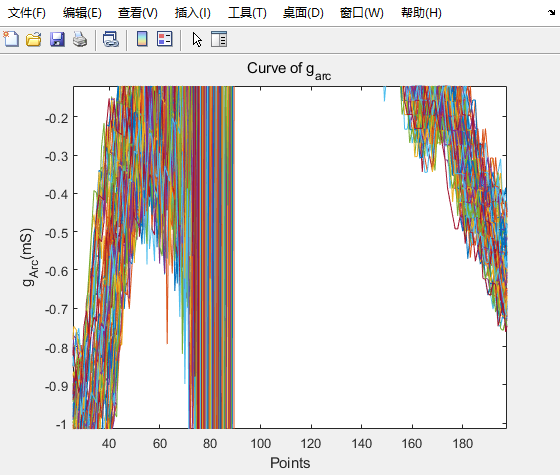
具体曲线放到过程如图

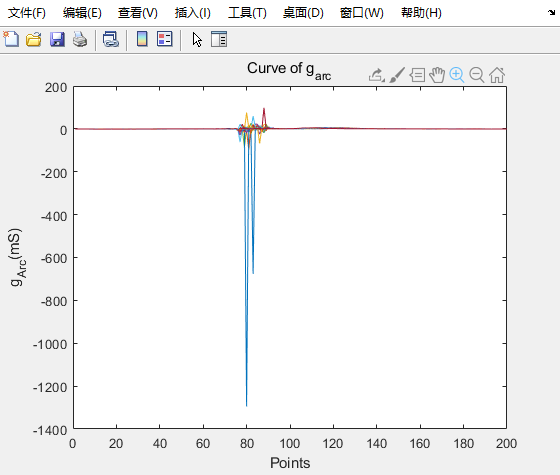
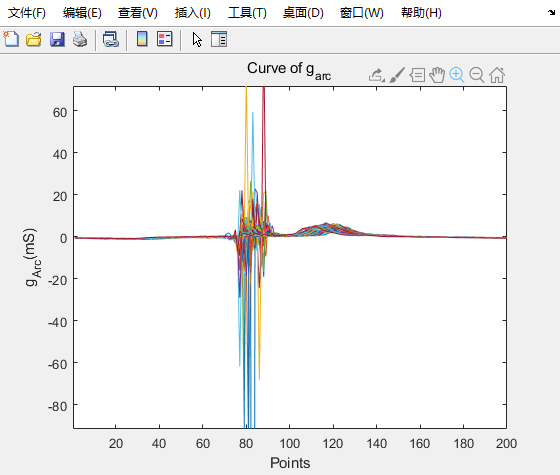
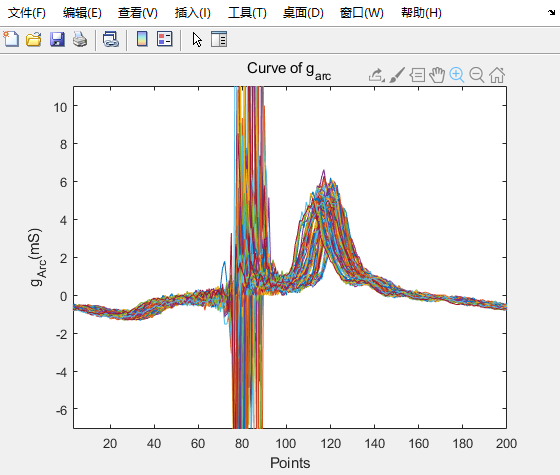
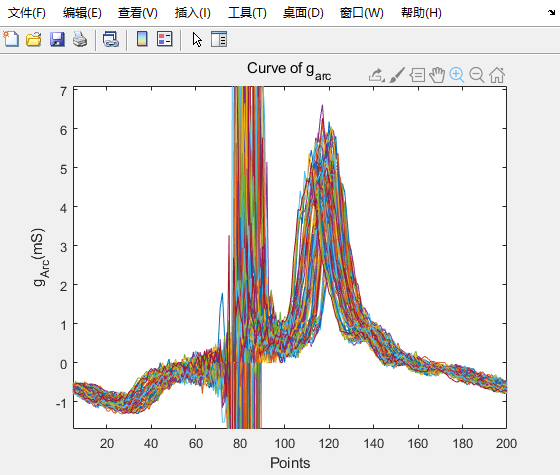
从50点积分到180点。