1. 从麦克斯韦方程组推导波动方程
其实导线和真空中电磁波的传播的波动方程是一致的,因为导线内并不存在电荷,整个导线是处于中性状态,故麦克斯韦方程组可以写为:
$\nabla \cdot E = 0\tag{1}$ $\nabla \cdot B = 0\tag{2}$ $\nabla \times E = - \frac { \partial B } { \partial t }\tag{3}$ $\nabla \times B = \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial E } { \partial t }\tag{4}$
对式(3)两边都去旋度。
$\nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E = - \frac { \partial } { \partial t } ( \nabla \times B )$
由于式(1),所以可以简写为
$0 - \nabla ^ { 2 } E = - \frac { \partial } { \partial t } ( \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial E } { \partial t } )$
这里用到一个矢量三重积公式:
$\nabla \times ( \nabla \times E ) = \nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E$
最后,波动方程为:
$\nabla ^ { 2 } E = \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial ^ { 2 } E } { \partial t ^ { 2 } }\tag{5}$
这里面把磁感应强度B消掉了,只包含电场E。
波速为$v = \frac { 1 } { \sqrt { \mu _ { 0 } \varepsilon _ { 0 } } }\tag{6}$
式(6)中,$\mu$是磁导率和$\varepsilon$是介电常数。
真空中的磁导率$\mu 0 = 4 \pi \times 10 ^ { - 7 } (N / A ^ { 2 })=1.2566371\times 10 ^ { - 6 } (N / A ^ { 2 })$ 真空中的介电常数$\varepsilon 0 = 8.854187818 \times 10 ^ { - 12}(F/m)$
铝导线中的磁导率$\mu_铝 = 1.256665\times 10 ^ { - 6 } (N / A ^ { 2 })$,与真空中的磁导率接近。
电磁波的传播和导线本身的介电常数不相关,和导线周围的环境相关,空气的节点常数接近真空,而土壤的介电常数则会大于真空。用真空中的介电常数去算对地电容,基本能够复合实验室测量结果。
需要研究这个电容,是如何等效成传统的对地电容的。
2. 场理论与传输线方程的等价性
上一章推导了波动方程,其假设条件是电磁波在真空中传播。假设沿z轴方向传播。再列写麦克斯韦方程。
$\left. \begin{array} { r l } { \nabla \times E _ { t } } & { = - j \omega \mu H _ { t } } \ { \nabla \times H _ { t } } & { = j \omega \varepsilon E _ { t } } \ { \nabla \cdot E _ { t } } & { = 0 } \ { \nabla \cdot H _ { t } } & { = 0 } \end{array} \right} \tag{2-1}$
其中,$\nabla$算子可表示为
$\nabla = \nabla _ { t } + \nabla _ { z } = \nabla _ { t } + e _ { z } \frac { \partial } { \partial z }\tag{2-2}$
麦克斯韦方程可写为
$\left. \begin{array} { c } {e _ { z } \times \frac { \partial E _ { 1 } } { \partial z } = - j \omega \mu H _ { 1 } } \ { e _ { z } \times \frac { \partial H _ { 1 } } { \partial z } = j \omega \varepsilon E _ { t } } \ { \nabla _ { 1 } \times E _ { i } = 0 } \ { \nabla _ { t } \times H _ { t } = 0 } \end{array} \right.\tag{2-3}$
通过矢量分析,可列写电压和电流的方程
$\left. \begin{array} { r l } { E _ { t } } & { = U ( z ) \nabla _ { 1 } \phi ( x , y ) } \ { H _ { t } } & { = I ( z ) \nabla _ { t } \psi ( x , y ) } \end{array} \right}\tag{2-4}$
对(2-3)前两式取旋度,可得
$\left. \begin{array} { c } { e _ { z } \times e _ { z } \times \frac { \partial ^ { 2 } E _ { 1 } } { \partial z ^ { 2 } } - \omega ^ { 2 } \mu \varepsilon E _ { 1 } = 0 } \ { e _ { z } ( e _ { z } \cdot \frac { \partial ^ { 2 } E _ { t } } { \partial z ^ { 2 } } ) - ( e _ { z } \cdot e _ { z } ) \frac { \partial ^ { 2 } E _ { 1 } } { \partial z ^ { 2 } } - \omega ^ { 2 } \mu \varepsilon E _ { 1 } = 0 } \end{array} \right.$
解得到
$\frac { \partial ^ { 2 } E _ { 1 } } { \partial z ^ { 2 } } + \beta ^ { 2 } E _ { t } = 0\tag{2-5}$
其中,$\beta ^ 2 = \omega^2 \varepsilon \mu$
同样可得
$\frac { \partial ^ { 2 } H _ { 1 } } { \partial z ^ { 2 } } + \beta ^ { 2 } H _ { i } = 0\tag{2-6}$
将(2-4)带入(2-5)和(2-6)中,得
$\left. \begin{array} { l } { \frac { d ^ { 2 } U } { d z ^ { 2 } } + \beta ^ { 2 } U = 0 } \ { \frac { d ^ { 2 } I } { d z ^ { 2 } } + \beta ^ { 2 } I = 0 } \end{array} \right.\tag{2-7}$
此即导出传输线波动方程。可以看出,在假设传输线中不产生电子运动情况下,用传统电路的分析方法是与场的分析方法等价的,而由于线路中确实不存在大量自由电子,所以用路的方法进行分析时可以有较高精度。
3. 时谐电磁波
将电磁波按照空间一维来表示,即表示空间中的某一点的幅值随时间的变化,即只有x轴和时间轴。
那么电场强度和磁场强度的变化可表示为复数形式
$\left. \begin{array} { l } { E ( x , t ) = E ( x ) e ^ { - i \omega t } } \ { B ( x , t ) = B ( x ) e ^ { - i \omega t } } \end{array} \right.\tag{3-1}$
代回到真空麦克斯韦方程组,可以得到。
$\left. \begin{array} { l } { \nabla \times E = i \omega E } \ { \mu \nabla \times B = - i \omega E } \ { \nabla \cdot E = 0 } \ { \nabla \cdot H = 0 } \end{array} \right.\tag{3-2}$
对式(3-2)中的第一式取旋度,同时结合第二式得到
$\nabla \times ( \nabla \times E ) = \omega ^ { 2 } \mu \varepsilon E\tag{3-3}$
带入矢量三重积,有
$\nabla \times ( \nabla \times E ) = \nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E = - \nabla \hat { E }$
$\nabla ^ { 2 } E + k ^ { 2 } E = 0\tag{3-4}$
其中$k = \omega \sqrt { \mu \varepsilon }$
考虑到$\nabla$算子的表达式,式(3-4)可以写作二阶微分方程
解出E后,可以用式(3-2)得到磁场B。
$B = - \frac { i } { \omega } \nabla \times E = - \frac { i } { k } \sqrt { \mu \varepsilon } \nabla \times E\tag{3-5}$
在固定频率下,麦克斯韦方程组可以写为以下方程
$\left. \begin{array} { c } { \nabla ^ { 2 } E + k ^ { 2 } E = 0 } \ { \nabla \cdot E = 0 } \ { B = - \frac { i } { \omega } \nabla \times E } \end{array} \right.$
类似的也可以写成以磁场为规划的方程组
$\left. \begin{array} { c } { \nabla ^ { 2 } B + k ^ { 2 } B = 0 } \ { \nabla \cdot B = 0 } \ { E = \frac { i } { \omega \mu \varepsilon } \nabla \times B = \frac { i } { k \sqrt { \mu \varepsilon } } \nabla \times B } \end{array} \right.\tag{3-6}$
4. 平面电磁波
将式(3-4)写成微分方程的形式,同样只考虑一维。
$\frac { d ^ { 2 } } { d x ^ { 2 } } E ( x ) + k ^ { 2 } E ( x ) = 0\tag{4-1}$
它的一个解是
$E ( x ) = E _ { 0 } e ^ { i k x }\tag{4-2}$
结合式(3-1)得
$E ( x , t ) = E _ { 0 } e ^ { i ( k x - \omega t ) }\tag{4-3}$
对于实际测量场强,只取实部,即实际测量电势
$E ( x , t ) = E _ { 0 } \operatorname { cos } ( k x - \omega t )\tag{4-4}$
这个公式的意义是在x轴上等于x处与时间t构成的平面上的一个波,也可以看作是沿x轴方向传播的平面波,当时间为0的时候,认为x=0时,$E=E_0$,处在波峰,在等于任意时间t时,波峰移至$k x - \omega t = 0$,即$x = \frac { \omega } { k } t$的平面上,因此平面波沿x轴的速度为
$v = \frac { \omega } { k } = \frac { 1 } { \sqrt { \mu \varepsilon } }\tag{4-5}$
对式(4-3)选择一个特殊坐标系,它的x轴沿电磁波传播方向,可以表示为式(4-6)
$E ( x , t ) = E _ { 0 } e ^ { i ( k \cdot x - \omega t ) }\tag{4-6}$
式中的$k$是一个矢量,当k的方向取x轴时,$k \cdot x = k x cos(\theta) = k x$,所以得到式(4-6).
对于式(4-6),必须满足$\nabla \cdot E = 0$才能得到电磁波,对式(4-6)取散度,有
$\nabla \cdot E = E _ { 0 } \cdot \nabla e ^ { i ( k \cdot x - \omega t ) } = i k \cdot E _ { 0 } e ^ { i ( k \cdot x - \omega k ) } = i k \cdot E = 0$
因此
$k \cdot E = 0\tag{4-7}$
上面表示E式横波,E可以在垂直于k的任意方向上震荡。E的取向称为电磁波的偏振方向,可以选与k垂直的任意两个互相正交的方向作为E的两个独立偏振方向,因此,对每一波矢量k,存在两个独立的偏振波。
平面电磁波的磁场可由式(3-5)求得,对(4-6)取旋度
$\nabla \times E = [ \nabla e ^ { i ( k \cdot x - a x ) } ] \times E _ { 0 } = i k \times E$
因此,
$B = \sqrt { \mu \varepsilon } \frac { k } { k } \times E = \sqrt { \mu } n \times E\tag{4-8}$
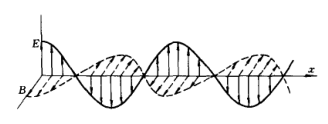
$n$为传播方向的单位矢量,由上式得$k \cdot B = 0$,因此磁场波动也是横波。$E、k、B$是三个互相正交的矢量。$E$和$B$同相位,振幅比为
| $ | \frac { E } { B } | = \frac { 1 } { \sqrt { \mu } \varepsilon } = v\tag{4-9}$ |
可得以下性质:
- 电磁波为横波,$E$和$B$都与传播方向垂直;
- $E$和$B$互相垂直,$E \times B$沿波矢$k$的方向;
- $E$和$B$同相位,振幅比为$\mu$。
平面电磁波传播方向各点上的电场和磁场的图如图所示。
5. 电磁波的能量密度-坡印廷向量
坡印廷矢量,也叫做能流密度矢量,其方向是电磁波能量的传输方向,大小为能流密度。其矢量的单位是瓦特每平方米$(W/m^2)$。
其矢量形式表示为:
$S = E \times H\tag{1}$
其中
$E$是电场强度 $H$是磁场强度
能流密度是标量,其表示形式为:
$u = \frac { 1 } { 2 } ( E \cdot D + B \cdot H )\tag{2}$
其中
$E$是电场强度 $D$是电位移矢量 $B$是磁感应强度 $H$是磁场强度
$D = \varepsilon E , H = \frac { 1 } { \mu } B$
实际上$u = \frac { 1 } { 2 } ( \varepsilon E \cdot E + \frac { 1 } { \mu } B \cdot B )$
$\varepsilon$是材料的电容率,即介电常数,空气磁导率和真空差不多,土壤中的磁导率和空气中区别较大。 $\mu$是材料的磁导率,在非磁材料中,磁导率基本一致
首先写出其对时间偏导的函数
$\frac { \partial u } { \partial t } = - \nabla \cdot S - J _ { f } \cdot E\tag{3}$
5.1 前提知识——三重积
$A \cdot ( B \times C ) = B \cdot ( C \times A ) = C \cdot ( A \times B )= - B \cdot ( A \times C )$
标量三重积代表的意义是体积
$\nabla \times ( \nabla \times E ) = \nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E$
矢量三重积的图形意义不明确。
5.2 坡印廷矢量的能流密度的推导
既然是矢量,那么该矢量就有散度和旋度,对坡印廷矢量取散度,并利用标量三重积进行运算。
$\nabla \cdot S = \nabla \cdot ( E \times H ) = H \cdot (\nabla \times E) = - E \cdot (\nabla \times H)\tag{4}$
麦克斯韦方程组中的第三项,表示变化的电场产生磁场。
$\nabla \times E = - \frac { \partial B } { \partial t }\tag{5}$
对两边取B的点积有
$B \cdot ( \nabla \times E ) = - B \cdot \frac { \partial B } { \partial t }\tag{6}$
麦克斯韦方程组中的第四项,表示变化的磁场会产生电场。
$\nabla \times H = \mu_0J + \varepsilon_0 \mu_0 \frac { \partial E } { \partial t }\tag{7}$
两边取E的点积有
$E \cdot ( \nabla \times B ) = E \cdot \mu _ { 0 } J + E \cdot \varepsilon _ { 0 } \mu _ { 0 } \frac { \partial E } { \partial t }\tag{8}$
引入标量三重积的恒等式
$- \nabla \cdot ( E \times B ) = E \cdot ( \nabla \times B ) - B \cdot ( \nabla \times E )\tag{9}$
将(6)和(8)带入(9)得
$- \nabla \cdot ( E \times B ) = E \cdot \mu _ { 0 } J + E \cdot \varepsilon _ { 0 } \mu _ { 0 } \frac { \partial E } { \partial t } + B \cdot \frac { \partial B } { \partial t }\tag{10}$
将坡印廷矢量的定义(1)改为电场强度和磁场强度形式
$S = E \times H = \frac { 1 } { \mu _ { 0 } } E \times B\tag{11}$
将(11)代回式(10)有
$\nabla \cdot S + \varepsilon _ { 0 } E \cdot \frac { \partial E } { \partial t } + \frac { B } { \mu _ { 0 } } \cdot \frac { \partial B } { \partial t } + J \cdot E = 0\tag{12}$
其中$J$表示导线中的电子流密度,在输电线中电子流很小。
可得围绕导线的坡印廷矢量的散度:
$\nabla \cdot S + \varepsilon _ { 0 } E \cdot \frac { \partial E } { \partial t } + \frac { B } { \mu _ { 0 } } \cdot \frac { \partial B } { \partial t }= 0\tag{13}$
对能流密度式(2)求偏导,结合式(11)可得坡印廷定理的微分形式
$\frac { \partial u } { \partial t } + \nabla \cdot S = - J \cdot E\tag{14}$
6. 有导体存在时的电磁波的传播
6.1 导体内的自由电荷
麦克斯韦方程组第一式,描述静电场性质。
$\nabla \cdot E = \frac { \rho } { \varepsilon _ { 0 } }\tag{6-1}$
其中,电荷密度为$\rho$。在电场作用下,形成电流$J$。
$J = \sigma E \tag{6-2}$
式中$\sigma$是电导率,带入(6-1)得
$\nabla \cdot J = \frac {\sigma} {\varepsilon} \rho \tag{6-3}$
根据电荷守恒定律,$\rho$的变化率为
$\frac { \partial \rho } { \partial t } = - \nabla \cdot J = - \frac { \sigma } { \varepsilon } \rho\tag{6-4}$
两面积分,解方程得
$\rho ( t ) = \rho _ { 0 } e ^ { - \frac { \sigma _ { t } } { \varepsilon } }\tag{6-5}$
$\rho_0$是$t = 0$时刻的电荷密度。由上式,电荷密度随时间指数衰减,衰减时间常数为$\tau$。
$\tau= \frac { \varepsilon } { \sigma }\tag{6-6}$
对于金属导线,$\tau$的数量级大约在$10^{-17}s$,电磁波频率50Hz,$\omega \ll \tau ^ { - 1 } = \sigma / \varepsilon$,即
$\underline { \sigma } \gg 1\tag{6-7}$
可以近似认为$\rho(t) = 0$,即导线可近似看作电磁波的良导体。良导体内部没有自由电荷,所有电荷分布在导体表面。
6.2 导体内的电磁波
对导体内部,$\rho = 0$,$J = \sigma E$,麦克斯韦方程组为
$\left. \begin{array} { l } { \nabla \times E = - \frac { \partial B } { \partial t } } \ { \nabla \times H = \frac { \partial D } { \partial t } + J } \ { \nabla \cdot D = 0 } \ { \nabla \cdot B = 0 } \end{array} \right.\tag{6-8}$
根据式(3-1)有
$\frac { \partial B } { \partial t } = - i \omega B$ $\frac { \partial E } { \partial t } = - i \omega E$
令$D = \varepsilon E , B = \mu H$,有
$\left. \begin{array} { l } { \nabla \times E = i \omega \mu H } \ { \nabla \times H = - i \omega \varepsilon E + \sigma E } \ { \nabla \cdot E = 0 } \ { \nabla \cdot H = 0 } \end{array} \right.$
与绝缘介质中的平面波方程组相比,只有第二项有区别,多了一项传导电流。
引入导体的“复电容率”
$\varepsilon ^ { \prime } = \varepsilon + i \frac { \sigma } { \omega } \tag{6-9}$
则,(6-8)的第二式可写为
$\nabla \times H = - i \omega \varepsilon ^ { \prime } E \tag{6-10}$
与真空中的平面波方程组一致,只是介电常数不同,所以
在式(6-8)第二项,右边两项分别代表位移电流和传导电流。传导电流与电场同向,它的耗散功率密度为$\frac { 1 } { 2 } \operatorname { Re } ( J ^ { * } \cdot E ) = \frac { 1 } { 2 } \sigma E _ { 0 } ^ { 2 }$。位移电流与电场有90°的相位差,但不消耗功率。在式(6-9)里,实数部分的$\varepsilon$代表位移电流的贡献,它不引起电磁波功率的耗散,虚数部分式传导电流的贡献,它引起能量耗散。
同样的,对于一定频率的电磁波,在导体内,满足亥姆霍兹方程。
$\nabla ^ { 2 } E + k ^ { 2 } E = 0 \tag{6-11}$
$k = \omega \sqrt { \mu \varepsilon ^ { \prime } } \tag{6-12}$
(6-11)也同样有平面波解
$E ( x ) = E _ { 0 } e ^ { i k \cdot x } \tag{6-13}$
k为复数,设
$k = \beta + i \alpha \tag{6-14}$
导体中电磁波的表示式为
$E ( x , t ) = E _ { 0 } e ^ { - \alpha \cdot x } e ^ { i ( \beta \cdot x - \omega t ) } \tag{6-15}$
其中,实部$\beta$描述波的传播的相位关系,虚部$\alpha$描述波的振幅衰减。$\beta$成为相位常数,$\alpha$成为衰减常数。
将式(6-14)和(6-9)带入(6-12)得
$k ^ { 2 } = \beta ^ { 2 } - \alpha ^ { 2 } + 2 i \alpha \cdot \beta = \omega ^ { 2 } \mu ( \varepsilon + i \frac { \sigma } { \omega } )\tag{6-16}$
比较式中实部与虚部有
$\left. \begin{array} { l } { \beta ^ { 2 } - \alpha ^ { 2 } = \omega ^ { 2 } \mu \varepsilon } \ { \alpha \cdot \beta = \frac { 1 } { 2 } \omega \mu \sigma } \end{array} \right. \tag{6-17}$
7. 磁流体动力学中的麦克斯韦方程组
磁流体动力学研究的是等离子体和磁场相互作用的物理学分支,磁流体力学中,等离子体被看作是良导体,假设磁场全部转化为电子流,而不转化为电场。
所以麦克斯韦方程写为:
$\left. \begin{array} { l } { \nabla \cdot E = \frac { \rho } { \varepsilon _ { 0 } } } \ { \nabla \times E = - \frac { \partial B } { \partial t } } \ { \nabla \cdot B = 0 } \ { \nabla \times B = \mu _ { 0 } J } \end{array} \right.$
与标准的麦克斯韦方程最主要的差别在第四项,标准的麦克斯韦方程组描述为。
$\left. \begin{array} { l } { \nabla \cdot E = \frac { \rho } { \varepsilon _ { 0 } } } \ { \nabla \cdot B = 0 } \ { \nabla \times E = - \frac { \partial B } { \partial t } } \ { \nabla \times B = \mu _ { 0 } ( J + \varepsilon _ { 0 } \frac { \partial E } { \partial t } ) } \end{array} \right.\tag{7-1}$
所以,结合导线内的电磁波传播分析中的式(6-9)有
$\varepsilon = i \frac { \sigma } { \omega } \tag{7-2}$
再与场路等价分析方法的麦克斯韦方程组进行对比有。
$\left. \begin{array}{l}{ \nabla \times E _ { t } = - j \omega \mu H _ { t } }\{ \nabla \times H _ { t } = j \omega \varepsilon E _ { t } }\{ \nabla \cdot E _ { t } = 0 }\{ \nabla \cdot H _ { t } = 0 }\end{array} \right. \tag{7-3}$
所以,若引入电弧,传统的电路分析方法是将电弧等效成一个可变电阻。
根据式(7-2),考虑空气中的电弧,我们可以看作当等离子体通道建立时,变化的磁场全部转换为电子和离子的相对运动,此时电压为0,而电流不为0。当等离子体通道不能维持时,电流能量转换为变化的磁场,而变化的磁场转换为变化的电场。而等离子体本身却是电中性的,将其看作是一个双端口的网络,那么其外特性可以看作是导线,而整体看就是一个开关。在整体分析上,仍然是场路等价的。
8. 传输线方程
重新仔细考虑传输线方程,
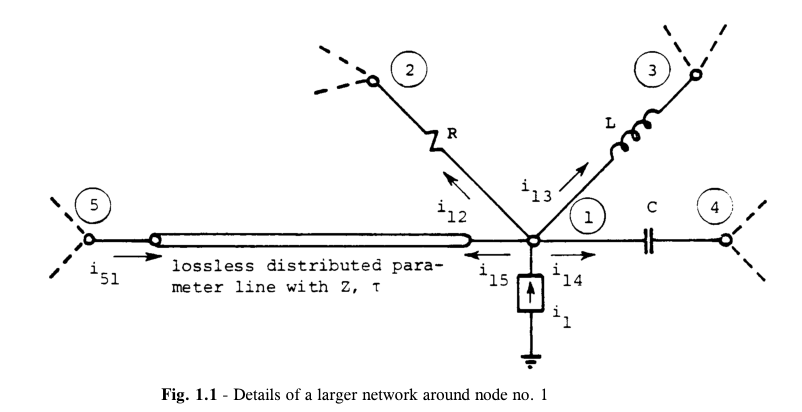
这是一个标准的电力网络,里面有电阻R、电感L、电容C、输电线路以及电流源激励。
\[i_{12}(t)+i_{13}(t)+i_{14}(t)+i_{15}(t)=i_{1}(t)\] \[i_{12}(t)=\frac{1}{R}\left\{v_{1}(t)-v_{2}(t)\right\}\] \[v=L \frac{d i}{d t}\] \[\frac{v(t)+v(t-\Delta t)}{2}=L \frac{i(t)-i(t-\Delta t)}{\Delta t}\] \[i_{13}(t)=\frac{\Delta t}{2 L}\left\{v_{1}(t)-v_{3}(t)\right\}+h i s t_{13}(t-\Delta t)\] \[h i s t_{13}(t-\Delta t)=i_{13}(t-\Delta t)+\frac{\Delta t}{2 L}\left\{v_{1}(t-\Delta t)-v_{3}(t-\Delta t)\right\}\] \[i_{14}(t)=\frac{2 C}{\Delta t}\left\{v_{1}(t)-v_{4}(t)\right\}+h i s t_{14}(t-\Delta t)\] \[h i s t_{14}(t-\Delta t)=-i_{14}(t-\Delta t)-\frac{2 C}{\Delta t}\left\langle v_{1}(t-\Delta t)-v_{4}(t-\Delta t)\right\}\]以上是电阻、电感、电容的计算方程,相对简单。
对于传输线,也就是node1~node5,先不考虑线路的阻抗损耗,则传输线方程为: \(-\frac{\partial v}{\partial x}=L^{\prime} \frac{\partial i}{\partial t}\)
\[-\frac{\partial i}{\partial x}=C^{\prime} \frac{\partial v}{\partial t}\]其中
$\mathbf{L}^{\prime}, \mathbf{C}^{\prime}$=单位长度传输线的电感和电容
x=从起始端的距离
传输线备注:
一个集中参数的传输线,若设单位距离很短,则可以近似用下图进行表示。
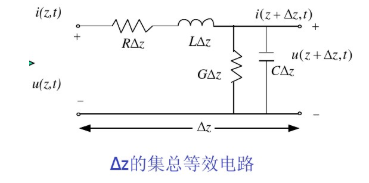
根据基尔霍夫定律有 \(u(z, t)-R \Delta z i(z, t)-L \Delta z \frac{\partial i(z, t)}{\partial t}-u(z+\Delta z, t)=0\)
\[i(z, t)-G \Delta z u(z+\Delta z, t)-C \Delta z \frac{\partial u(z+\Delta z, t)}{\partial t}-i(z+\Delta z, t)=0\]改写成微分方程形式 \(\frac{\partial u(z, t)}{\partial z}=-R i(z, t)-L \frac{\partial i(z, t)}{\partial t}\)
\[\frac{\partial i(z, t)}{\partial z}=-G u(z, t)-C \frac{\partial u(z, t)}{\partial t}\]若忽略线路电阻和对地电导,则有 \(\frac{\partial u(z, t)}{\partial z}=-L \frac{\partial i(z, t)}{\partial t}\)
\[\frac{\partial i(z, t)}{\partial z}=-C \frac{\partial u(z, t)}{\partial t}\]在分析传输线问题时,用“路”理论会引入另一条导线,也就是地线,所有的分析,电压是对地线的电压,电流要通过地线形成回路,这与实际情况不相符。
9. 导线对地电容的计算
导线对地电容的计算方法是Carson在1926年提出的,其理论假设为在大地里预设大地电流回路。
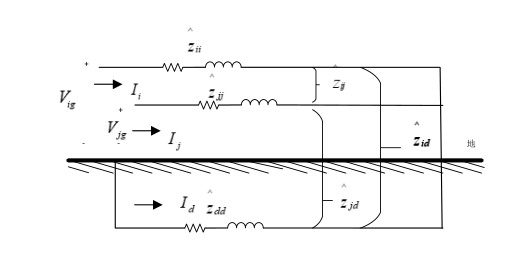
其导线对地电容则看作是架空线路和大地回路两导线间的感应电容。
而实际上并不存在大地回路,架空线所表现出的分布式电容特性是有导体存在下的麦克斯韦方程组中的第4项中,变化的磁场可转换为变化的电场+带电粒子流动,分别代表位移电流和传导电流。
$\nabla \times B = \mu _ { 0 } ( J + \varepsilon _ { 0 } \frac { \partial E } { \partial t } ) \tag{9-1}$
变化的电磁场在导体内形成的传导电流即表现出导线的阻抗特性,而位移电流与电场有90°的相位差,不消耗功率,即导线体现出的电容特性,其电容特性完全由“复电容率”所体现。
现在有2种主要的解释方式,一种是能量是通过电磁波的方式在导线周围空气中传播的,导线只是引导了传播的通道。另一种解释是电磁波在导线内传播,主要是变化的磁场集中于导线内部,在导线内部转换成电子的流动,从而传播能量。也就是以磁场的变化率形式存在还是以电子流的形式存在,或者是共存状态。
参考《关于金属介电常数的讨论》
在此情况下,$\varepsilon _ { r } = \varepsilon _ { r } ^ { \prime } + i \frac { \sigma } { \varepsilon _ { 0 } \omega }$的实部部分$\varepsilon _ { r } ^ { \prime }$并不为0。
可以进行大概的计算,取光波$\lambda = 3000$,$\omega _ { 0 } \approx 314$
$\varepsilon _ { r } ^ { \prime } = 1 + \frac { N e ^ { 2 } } { m \varepsilon _ { 0 } } \sum _ { j = 1 } ^ { K } \frac { f _ { j } } { \omega _ { j } ^ { 2 } } = 1 + \frac { 10 ^ { 29 } \times ( 1.6 \times 10 ^ { - 19 } ) ^ { 2 } } { 9.1 \times 10 ^ { - 31 } \times 8.85 \times 10 ^ { - 12 } \times ( 6 \times 10 ^ { 15 } ) ^ { 2 } } \approx 10$
结果大约是金属中的位移电流的介电常数约10倍的空气中的介电常数。
真空中的介电常数$\varepsilon 0 = 8.854187818 \times 10 ^ { - 12}(F/m)$
空气中的介电常数与真空中近似相等,电磁波传输3.5km,等效电容约$3.1 \times 10 ^ {-8}F$,按照集中参数计算容流约0.168A。
在武汉试验场进行数据测定,一条三相的3.5km长的架空线路产生的接地电流为测量两次,分别为0.144A和0.163A,在数量级上是相等的。
通过测定可以看出来,架空线上的能量主要还是通过架空线周围的空气进行传播的。
电缆的电磁波介电常数估计,按照电缆周围是电缆沟环境,旁边的电磁波传输介质为空气,土壤环境,土壤是由空气、固体和水组成的多孔介质,其中水的介电常数大约是80,固体的介电常数大约是4,而空气的介电常数大约是1,所以土壤的介电常数会介于4~80之间。
400的三芯电缆560m,测量到的产生的接地电流两次,分别是1.13A和1.24A。转换成介电常数约$3.71 \times 10 ^ {-10}(F/m)$~$4.07 \times 10 ^ {-10}(F/m)$
约架空线路的50倍,负荷估计预期。
这里由于电缆沟的环境复杂,还需要一些精确计算的手段。
利用Cason公式计算结果
利用Cason公式计算结果,架空线表现介电常数为$1.35 \times 10 ^ (-10)(F/m)$,是$\varepsilon 0 = 8.854187818 \times 10 ^ { - 12}(F/m)$的15倍,Cason公式的计算误差较大。
10. 利用场的方法进行电磁暂态仿真计算
$\frac { \partial ^ { 2 } E _ { 1 } } { \partial z ^ { 2 } } + \beta ^ { 2 } E _ { t } = 0\tag{2-5}$
其中,$\beta ^ 2 = \omega^2 \varepsilon \mu$
同样可得
$\frac { \partial ^ { 2 } H _ { 1 } } { \partial z ^ { 2 } } + \beta ^ { 2 } H _ { i } = 0\tag{2-6}$
用电磁场的波动方程进行电磁暂态仿真计算。