Comsol等离子体模块使用手册

2. 等离子体模型所需数据

低温等离子体的建模不仅因为发生了大量的物理过程，而且还因为需要提供给模型的数据量很大，因此建模很困难。本章概述了在尝试对等离子体建模之前需要收集的数据。

2.1 所需数据

本节概述了在尝试对等离子体建模之前要组装的数据。

主要困难之一是为感兴趣的等离子体找到完整且物理上正确的化学机制。这可能只涉及少数反应和物种（如氩气），或者在分子气体的情况下，可能有数百个反应和数以百计的物种。通常可以从文献搜索中找到化学机制，但如果它是一种独特的等离子体化学，那么化学机制可能是未知的。唯一的选择是找到一种与您的特定应用具有相似特性的等离子体化学物质并将其用作参考。

以下部分将指导您了解构成等离子模型的每个特征的数据需求。

2.1.1 电子撞击反应

对于每个电子碰撞反应，反应公式是需要的第一条信息。大多数已发表的涉及等离子体数值建模的论文都包含一个组成等离子体化学反应的表格。

输入公式后，您需要提供一些数据来表明反应速率对电子能量的依赖性。实现这一点的最常见方法是为每个电子碰撞反应指定横截面数据。横截面数据可能很难找到，甚至不存在。目前已经得到了对于大多数常见气体的横截面数据。以下链接提供了一些有用的横截面数据资源：

https://fr.lxcat.net/home/

横截面数据必须采用特定格式才能导入 COMSOL Multiphysics。请参阅导入碰撞横截面数据。

如果横截面数据不可用，则可以使用常数值、Arrhenius 表达式或查找表指定速率系数。对于 Arrhenius 表达式，必须指定 Arrhenius 系数。如果要使用速率系数查找表，则需要加载速率或汤森系数与平均电子能量的表。

根据电子碰撞碰撞的类型，还需要以下数据：

用于弹性碰撞的电子与目标物质的质量比。
非弹性碰撞的能量损失（以 eV 为单位）。
如果需要详细的平衡，目标和生产物种之间的统计权重比。

DETAILED BALANCE细节平衡？

如果需要详细的平衡，则创建逆反应的横截面数据。所以，假设你有一个电子激发反应，比如：

$e+Ar=>e+Ars$

并且您还希望在模型中包含逆反应：

$e+Ars=>e+Ar$

然后可以重新使用正向反应的横截面数据来计算逆向反应的横截面数据。为了构建详细的平衡，需要目标和产品种类之间的统计权重比。用于计算逆反应横截面数据的公式首先将电子能量数据 ε 移动激发能量 Δε ，$ \varepsilon \rightarrow \varepsilon+\Delta \varepsilon $然后将横截面数据 σ 按统计权重的比率 g 缩放 ,$ \sigma \rightarrow \sigma / g $ . 这形成了一个新的碰撞截面与逆反应能量的查找表。在实践中，所使用的值不应对总排放量产生太大影响特征。一些气体的数据可以在参考文献2中找到。

2.1.2 反应

对于气相反应，需要使用 Arrhenius 系数或数值数据的正向速率常数。如果反应是可逆的，则以相同的方式输入反向速率常数。

2.1.3 界面反应

对于表面反应，需要以下数据：

正向粘附或速率系数，可以是数值或根据阿累尼乌斯参数指定为表面温度的函数。
对于一级反应，需要总表面位点浓度。
对于导致发射二次电子的表面反应，需要二次发射系数和二次电子的平均能量。

2.1.4 类

对于每个重species，都需要以下信息：

物种的分子量
物种的潜在特征长度；需要计算正确的扩散率和迁移率
物种的势能最小值；需要计算正确的扩散率和迁移率

如果您有兴趣求解中性气体温度，则需要以下附加信息：

物种摩尔焓、熵和比热，可以直接作为温度的函数或使用 NASA 多项式输入
在电子激发的物质或离子的情况下，可以输入基态物质的性质，也可以输入对物质焓的额外贡献

等离子体模块为以下物种提供预定义的传输和热力学数据：

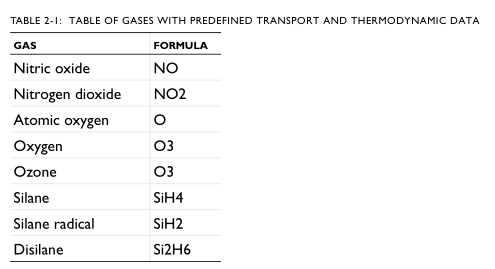
还预定义了以下表面物种属性：

许多其他物种的热力学和传输特性可以在以下链接中找到：

• Thermodynamic properties: http://burcat.technion.ac.il/dir/THERM.DAT • Transport properties: http://uigelz.eecs.umich.edu/pub/data/e_reactions.pdf • Additional transport properties: http://combustion.berkeley.edu/gri-mech/ version30/files30/transport.dat

2.2 导入碰撞横截面数据

为了简化建模过程，所有多物理场接口和玻尔兹曼方程、两项近似接口都可以从文件中导入碰撞截面集。本节详细介绍了所需的文件格式并包含以下主题：

横截面数据文件格式
文件格式
等离子模块横截面数据要求的参考资料

3. AC/DC 接口

在本章中有

静电接口
电流接口
电路接口
静电接口理论
电流接口理论
电路接口理论
连接到电路
材料导入

3.1 静电接口

静电学 (es) 接口在添加物理场接口时位于 AC/DC 分支下，用于在明确电荷分布的条件下计算电介质中的电场、电位移场和电势分布规定。除了与其他物理场接口一起使用外，该公式是固定的。所有空间维度都支持特征频率、频域、小信号分析和时域建模。

物理场接口使用标量电势作为因变量来求解电场的高斯定律。

电荷守恒是主要节点，它添加了电势方程，并具有一个设置窗口，用于定义电位移场的本构关系及其相关属性，例如相对介电常数。

添加此物理场接口后，这些默认节点也会添加到模型开发器中 - 电荷守恒、零电荷（默认边界条件）和初始值。然后，从物理工具栏中，添加实现边界条件和空间电荷等其他节点。您也可以右键单击静电以从上下文菜单中选择物理特性。

3.1.1 静电接口的域、边界、边、点和对节点

不同介质界面处的相关物理界面条件为

$ \mathbf{n}{2} \cdot\left(\mathbf{D}{1}-\mathbf{D}{2}\right)=\rho{\mathrm{s}} $

在没有表面电荷的情况下，该条件由自然边界条件满足

$ \mathbf{n} \cdot\left[\left(\varepsilon_{0} \nabla V-\mathbf{P}\right){1}-\left(\varepsilon{0} \nabla V-\mathbf{P}\right){2}\right]=-\mathbf{n} \cdot\left(\mathbf{D}{1}-\mathbf{D}_{2}\right)=0$