2020-04-11-基于土壤电离能平衡的电流相关接地电阻模型

Current-Dependent Grounding Resistance Model Based on Energy Balance of Soil Ionization

摘要

当土壤中的电流密度超过临界值并降低接地电阻时，土壤电离会在接地电极周围发生。 本文提出了一种考虑土壤电离的电流相关接地电阻模型。提出的模型是基于土壤电离的能量平衡得出的。 电离区的电阻率取决于该区中存储的能量。 提出了该模型的解析表达式以估计区域电阻率。 通过与实验结果进行比较来验证该模型。

1. 引言

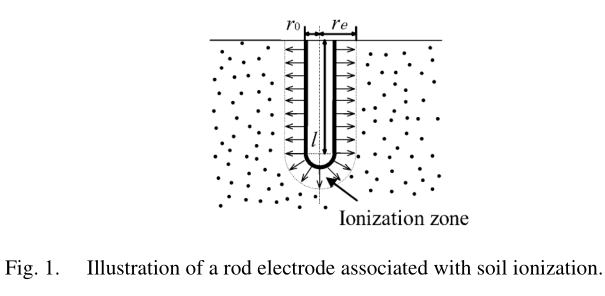
接地电阻随着注入电流的增加而减小。 这种现象是由接地电极周围的土壤电离引起的[1] – [11]。 研究了考虑土壤电离的两种计算非线性接地电阻的方法。 第一个考虑了土壤电离区的电阻率和尺寸。 另一个是根据电压-电流曲线的经验关系确定的[12]。 Bellaschi引入了有效半径和长度，该半径和长度取决于从动杆的注入电流，以估算接地电阻的电流依赖性。如图1所示，低电阻率的离子化区域随注入电流的增加而增长。假设该区域的电阻率为零，Bellaschi模型可方便地估计与电流有关的接地电阻。 但是，区域电阻率不会突然变为零。Liew和Darveniza提出了一个动态接地电阻模型，该模型考虑了区域电阻率和磁滞效应[4]。 他们模型中的区域电阻率是时间和电流密度的函数。 使用Liew-Darveniza模型的计算结果与实验结果令人满意。 但是，该模型的物理含义和推导并未充分提及。

土壤电离受许多因素影响，例如土壤电阻率，温度和水分含量。 考虑到土壤电离类似于放电[13]，土壤电离应根据能量平衡来表示，该能量平衡将输入能量与电阻率的变化相关联。用经验公式来表示接地电阻的电流依赖性与所施加电流的峰值之间的关系，以用来模拟传输线的过电压[14]。 该公式没有考虑滞后效应，并且使用该公式进行的仿真结果表明小波的精度较低。 因此，应该开发一个更准确的模型来考虑影响接地电阻的参数。 本文提出了一种基于土壤电离能平衡的电流相关接地电阻模型。 所提出的模型由电极尺寸，注入电流和电离区中存储的能量确定。 推导并讨论了模型的解析表达式。 一位作者对高脉冲电流的接地电阻进行了许多实验[7] – [9]。 通过与实验结果进行比较验证了所提出的模型。

2. 电阻R的电流-D相关接地电阻的测量结果

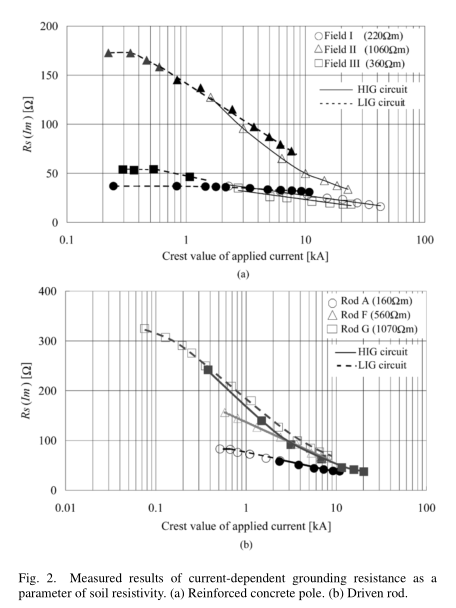
图2显示了高脉冲电流下钢筋混凝土杆（半径mm，长度m）和从动杆（mm，m）的测量接地电阻[9]。 由于时间依赖性和土壤电离的固有滞后效应，到达峰值的电压与施加的电流的峰值不一致。 本文对高脉冲电流采用以下接地电阻定义[8]

\[R _ { s } \left( I _ { m } \right) = \frac { V _ { m } } { I _ { m } }\tag{1}\]

其中，$V_m$是峰值电压，$I_m$是峰值电流，$R_s$是接地电阻的变化。

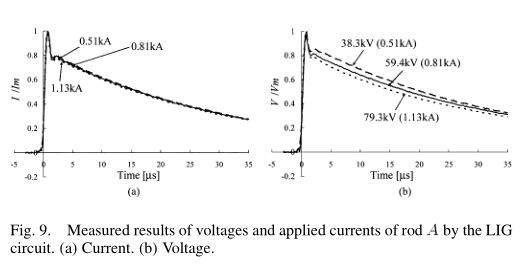
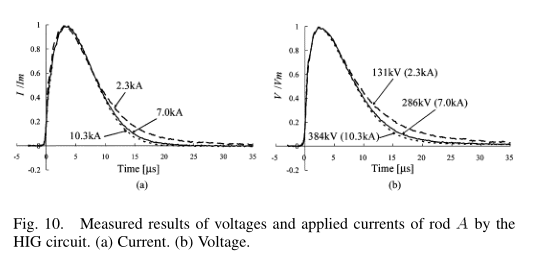
图2中的低脉冲电流发生器（LIG）电路与高脉冲电流发生器（HIG）电路不同，这是因为存在阻尼电阻器，该电阻器连接在测试的接地电极和电流引线导体之间 降低HIG电路的电流。 LIG电路的电流波形与HIG电路的电流波形通过阻尼电阻不同，如附录A所示。图2中的土壤电阻率是使用表[4]根据表I中所示的未土壤化的测得的稳态接地电阻估算的 。

\[R _ { s } = \frac { \rho _ { 0 } } { 2 \pi l } \ln \left( 1 + \frac { l } { r _ { 0 } } \right)\tag{2}\]

其中，$\rho_0$是不考虑土壤电离的电阻率。

实际的土壤电阻率不是均匀分布的，图2（b）中的电阻率不同于图2（a）中的电阻率。

从图2可以明显看出，接地电阻很大程度上取决于施加电流的峰值，尽管土壤电阻率不同，但对于10 kA以上的高脉冲电流，接地电阻几乎变为相同的值。

土壤的电阻率变化是随着电流的值的变化而动态变化的，那么单相接地电阻

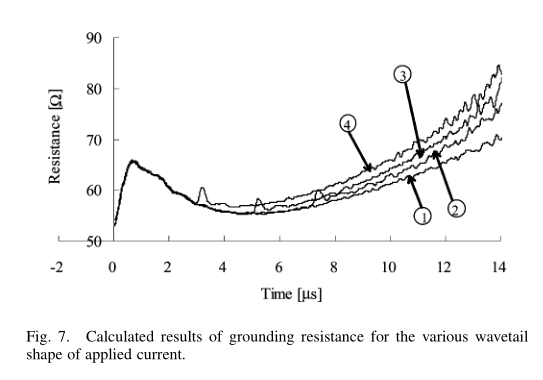
图3显示了杆的测量结果，即施加的电流，杆电压和接地电阻时间波形。 给出了所有施加电流的几种波形的所有波形[9]。 接地电阻时间函数定义为瞬时杆电压与同一时刻施加的电流之比。 波形1是由HIG电路产生的，而波形2至4是通过改变棒-棒间隙的长度和电阻器的值来控制的，这些值串联在脉冲发生器的顶部和接地之间。

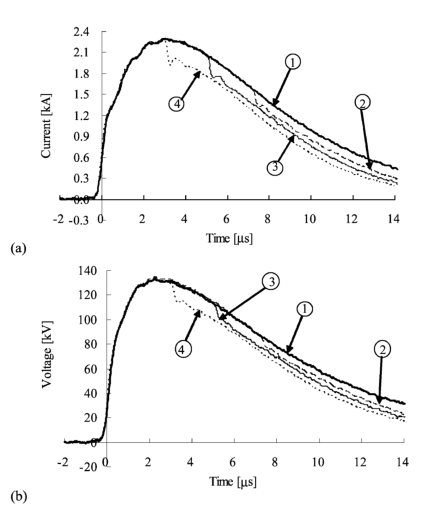
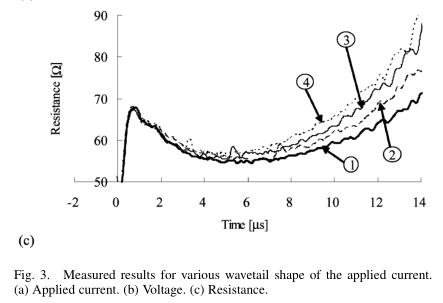
如附录II所示，使用带有步进电流的脉冲发生器测量的杆的接地电阻的时间常数约为1 s。 这个时间常数足够短，比在波形中施加电流改变之后的持续时间要短，对于粗略估计，接地电阻的瞬态特性可以忽略不计。 因此，接地电阻的差异受电流波形的影响，区域电阻率取决于波形。

3. 基于土壤电离的能量平衡的基于电流接地电阻模型

接地电阻的非线性表现为土壤电离区的增加和区域电阻率的变化。 参考文献[13]通过观察X射线胶片上的放电来描述电离区的发展，该胶片设置在接地电极下方进行测试。 观察结果表明，电离区的发展表现出与空气中放电相似的特征。参考文献[6]研究了许多关于土壤电离的论文，并支持土壤电离与空气电离分解之间的相似性。 能量平衡是推导所有描述放电过程的模型的基础。 因此，土壤电离可以看作是一种放电，而区域电阻率应根据土壤电离的能量平衡来确定。

A. 增加土壤电离区

每当电流密度通过电极分支并超过临界值时，就会发生土壤电离。 随着注入电流的增加，其电阻率远低于初始土壤电阻率的土壤电离区会增长。 临界注入电流$I_c$与土壤电离梯度$E_c$的关系。

\[E _ { c } = \rho _ { 0 } \frac { I _ { c } } { S \left( r _ { c } \right) }\tag{3}\]

其中，$S(r_c)$是离接地电极一定距离$r_c$的电离区的表面积。

用（3）代入来确定波前瞬时注入电流的电离区轮廓。 大电流的接地电阻在波尾中显示出较低的值[8]。 所提出的模型假定即使注入电流变得低于峰值，电离区仍保持其轮廓。

B. 土壤电离区的电阻率变化

由于放电，土壤电离区的电阻率降低。 通过选择适当的模型，可以简单地估算与电流相关的接地电阻，其中将区域的电阻率假定为零。 但是，电阻率不会突然变为零，而是取决于诸如电流密度，时间常数[3]，水含量[15]和温度[8]之类的因素。 接地电阻在小波中逐渐恢复其初始值。 这一事实表明，在土壤去离子过程中，电离区的电阻率增加了。

C. 土壤电离的能量平衡

每次放电的能量平衡由[16]给出

\[\frac { d Q } { d t } = u i - P\tag{4}\]

其中

$u$ 放电电压(V/m) $i$ 放电电流(A) $Q$ 累积能量(J/m) $P$ 能量损耗(W/m) $t$ 时间(s)

可以认为土壤电离过程类似于在电流中断期间断路器内部发生的电弧现象。 因此，在准确模拟接地系统的土壤电离的努力中，可以利用在开关电弧建模方面积累的国际经验。 因此，Mayr方程[17]是处理能量平衡的结果（4）

\[g = K \exp \left( \frac { Q } { Q _ { 0 } } \right)\tag{5}\]

其中g是电弧电导（Sm），K和$Q_0$是常数，基于可应用的能量平衡方程描述电弧的演化机理，并推导以下微分方程：

\[\frac { 1 } { g } \cdot \frac { d g } { d t } = \frac { 1 } { Q _ { 0 } } ( u i - P )\tag{6}\]

功率损耗主要由散热/传导产生，应表示为温度和焓的函数。 考虑到离电极的距离越长，电离区中的温度可能会变得越低，热量损失会移到电离区之外。 这种传导会产生功率损耗。 因此，根据Cassie的弧形模型[18]，所提出的模型中的功率损耗被假定为与分段的表面积成比例。 功率损耗为

\[P = \lambda S\tag{7}\]

D. 计算接地阻抗

公式（6）应同时用外部电路求解。注入电流at是计算中的一个时间步长，它是通过在数字仿真中选择一个小电流而得出的精确电流的近似解。 提出的模型中的电流可以通过采用来视为外力。 因此，可以使用处的电压和电流将接地电导估计为（6）的解。 电流相关的接地电阻通过将每个段的电阻相加得出

\[R _ { s } ( i ) = \int _ { r _ { 0 } } ^ { r _ { c } } g ^ { - 1 } ( r ) d r + \int _ { r _ { e } } ^ { \infty } g ^ { - 1 } ( r ) d r\]

其中r是离接地电极的距离（m），$r_e$是电离区的有效半径，g(r)是r处的电导。

当电阻率达到初始值时，提出的模型将停止计算分段的电阻率。忽略（8）中的第一项给出一个简单的模型。考虑到接地电极附近的电阻率会影响接地电阻，因此该简单模型需要较高的土壤电离梯度，因此使用该简单模型计算的结果与实验结果吻合[6]，[9]。

4. 土壤电离区的电阻率的近似表达式和一般表达式

微分方程可以在一个假设条件下解析求解。 本章描述了所提出模型的解析表达式。

A. 模型的近似表达

电弧起弧后，其电功率输入与电阻率大致保持恒定，随着电弧电流的增加而迅速减小[19]。 该过程类似于土壤电离的过程。 假设输入的电功率与电导无关，则土壤电离区的电导和电阻率表示如下：

\[g = g _ { 0 } \exp \left( \frac { E _ { n } - N } { Q _ { 0 } } \right)\tag{9}\] \[\rho = \rho _ { 0 } \exp \left( - \frac { E _ { n } - N } { Q _ { 0 } } \right)\tag{10}\]

其中，$E _ { n } = \int u i d t[ \mathrm { J } / \mathrm { m }$，$N = \int p d t [ \mathrm { J } / \mathrm { m } ]$，$g_0$是初始电导。因此所提出的模型显示出能量依赖性，并考虑了电压和电流波形的影响。 图4示出了土壤电离区的电阻率$\rho$的曲线。 当注入电流超过临界电流时，电阻率将减小。在注入电流开始减小之后，电阻率不会迅速增加，因为存储在该段中的能量会持续增加一段时间。 土的去离子过程中电阻率逐渐增加。 结果，接地电阻显示出磁滞特性。 在实验结果中观察到了这一特征[8]。

等式（8）和（10）表明所提出的模型具有以下物理意义。

1. 电流依赖性：注入电流越高，土壤电离区越大。 该区域的增长等同于有效半径的增加，并且会减小接地电阻。
2. 能量依赖性：随着区域中存储的能量的增加，区域电阻率会降低。
3. 土壤去离子：当功率输入小于功率损耗时，区域电阻率增加，最后，降低的电阻率将恢复初始值。
4. 磁滞效应：注入电流达到峰值后，区域电阻率会持续下降一段时间，并在土壤去离子过程中逐渐增加。 电离过程中的区域电阻率曲线与去离子过程中的区域电阻率曲线不同。 因此，电阻率显示出磁滞特性。

4. 模型的一般表达式

考虑到关系式$i = gu$（6）可以解决，并且电导率和电阻率由下式给出

\[g = g _ { 0 } \exp \left( \frac { - t } { \tau } \right) \left[ 1 + \frac { 1 } { g _ { 0 } Q _ { 0 } } \int i ^ { 2 } \exp \left( \frac { t } { \tau } \right) d t \right]\tag{11}\]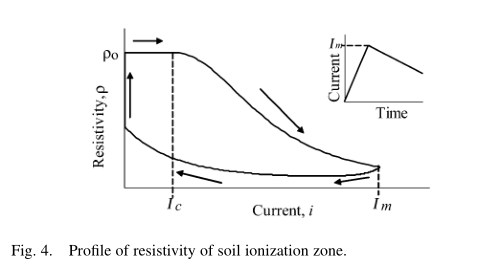

\[\rho = \rho _ { 0 } \exp \left( \frac { t } { \tau } \right) \left[ 1 + \frac { 1 } { g _ { 0 } Q _ { 0 } } \int i ^ { 2 } \exp \left( \frac { t } { \tau } \right) d t \right] ^ { - 1 }\tag{12}\]

其中$t$是土壤电离后的时间常数，$\tau = Q _ { 0 } / P [ \mathrm { s } ]$

\[\rho = \rho _ { i } \exp \left( \frac { t ^ { \prime } } { \tau } \right)\tag{13}\]

其中，$t ^ { \prime } = 0$，电流等于零。式（13）表示恢复初始值时的电阻率的时间常数。

等式（11）和（12）包括一个散度函数$\exp ( t / \tau )$，并且对一般表达式的计算经常导致数值散度。 附录III描述了一种计算（11）和（12）的方法。

5. 讨论

A. 提出的模型与Liew-Darveniza模型的比较

设置$(ui - P)/Q_0 = \alpha(constant)$，(10)可以写成：

\[\rho = \rho _ { 0 } \exp ( - \alpha t )\tag{14}\]

方程（14）与土壤电离过程中的Liew-Darveniza模型相同。 另一方面，去离子过程中的Liew-Darveniza模型由下式给出：

\[\rho = \rho _ { i } + \left( \rho _ { 0 } - \rho _ { i } \right) \left( 1 - \exp \frac { - t } { \tau _ { 2 } } \right) \left( 1 - \frac { J } { J _ { C } } \right) ^ { 2 }\tag{15}\]

其中

$\tau_2$ 去离子时间常数(s) $J$ 当前密度(A/m^2) $J_c$ 临界电流密度 $\rho_i$ 电流衰减时的电阻率与电离过程中的电阻率不同。

当$J=0$时，（15）

\[\rho = \rho _ { i } + \left( \rho _ { 0 } - \rho _ { i } \right) \left( 1 - \exp \frac { - t } { \tau _ { 2 } } \right)\tag{16}\]

公式（16）和公式（13）不同，时间常数$\tau_d$被定义为

\[\tau _ { d } = \int _ { 0 } ^ { T } \left( 1 - \frac { \rho } { \rho _ { 0 } } \right) d t\tag{17}\]

其中T时当$\rho$到$\rho_0$的时间T，引入以比较电阻率的瞬态特性。用（13）代入土壤去离子的时间常数。$T = \tau ln ( \rho_0 / \rho_i )$，不太好写，直接截图吧。

考虑到k足够小，小于unity，如果采用相同的值，Liew-Darveniza模型的去离子时间常数是所提出模型的去离子时间常数的几倍。 因此，使用较大的去离子时间常数，电阻率从最低值到Liew-Darveniza模型的初始值的变化几乎与所提出的模型相同。 因此，Liew-Darveniza模型是提出的模型的一种，而提出的模型提供了其模型的物理含义。

B. 提出模型的常数

1. 土壤电离梯度：建议为300 kV / m [6]，400 kV / m [14]和1000 kV / m [5]。 因此，该值不成立。 应该选择一个较低的值来考虑土壤电离区的电阻率。
2. 功率损耗：当土壤电离刚开始时，即等于$i = I_c$。 因此，从（10）起应满足以下关系： \(( u i - P ) _ { i = I c } = 0\tag{19}\) 从（3），（7）和（19），获得以下关系： \(\begin{aligned} u I _ { c } - P & = S \left( \frac { E _ { c } ^ { 2 } } { \rho _ { 0 } } - \lambda \right) = 0 \\ \therefore \lambda & = \frac { E _ { c } ^ { 2 } } { \rho _ { 0 } } \end{aligned}\tag{20}\) 当输入功率大于临界值时，可以认为发生土壤电离。
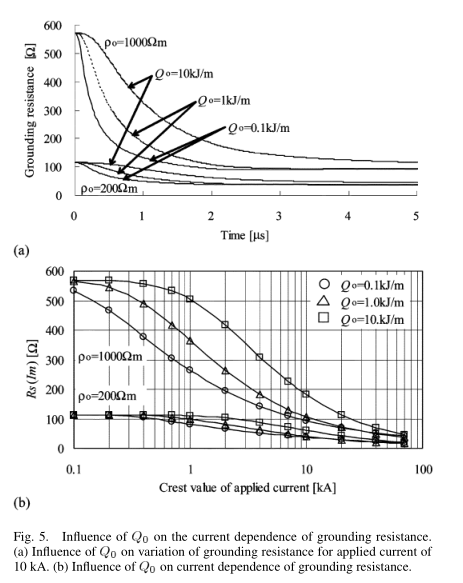
3. 图5显示了使用和的参数测量接地电阻时间演变的计算结果，其中所施加的电流具有2/40us和$E_c = 300kV / m$的斜坡波形。

土壤电离的时间常数与。因此，接地电阻越小则下降越快，最后变为与图5（a）所示几乎相同的值。 图5（b）表示，接地电阻的电流依赖性越小则越大，但施加的电流越高则接地电阻的影响越小。

C. 计算结果与实验结果比较中所提议模型的验证

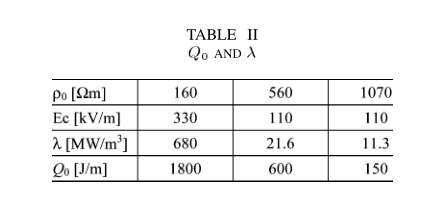
图6和图7给出了图2(b)和图3(c)所对应的接地电阻的计算结果。模型的常数如表二所示，其中为线段的宽度。接地电阻的时间依赖性由图12(b)中的等效电路表示。假设电路各电阻的电流依赖性与总接地电阻的电流依赖性成正比，而等效电路的电容不依赖于电流。由Liew - Darveniza计算的结果包括在图6中。

计算结果与实测结果的对比表明，该模型具有较好的精度。测量结果与计算结果的差异可能是由式(7)中能量损耗的简化假设和等效电路的时间依赖性造成的。Liew-Draveniza模型对于小电流具有足够的准确性，因为其模型的误差随着外加电流的增加而增加。

\[\tau _ { d } = \left\{ \begin{array} { l l } \tau [ - \ln k - ( 1 - k ) ] & \approx \tau \sum _ { n = 2 } ^ { \infty } \frac { ( 1 - k ) ^ { n } } { n } ; \text { proposed model } \\ \tau _ { 2 } ( 1 - k ) ; & \text { Liew-Darveniza model } \end{array} \right.\tag{18}\]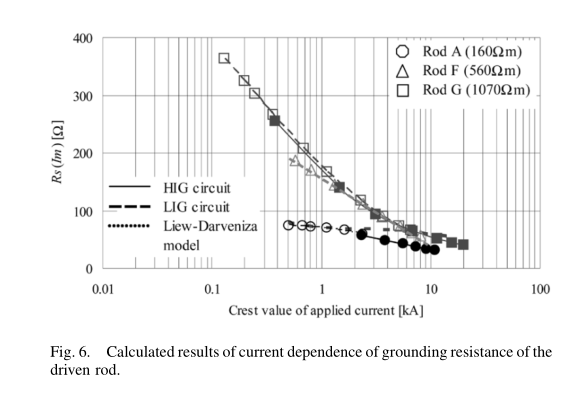

D. 近似表达式与一般表达式的比较

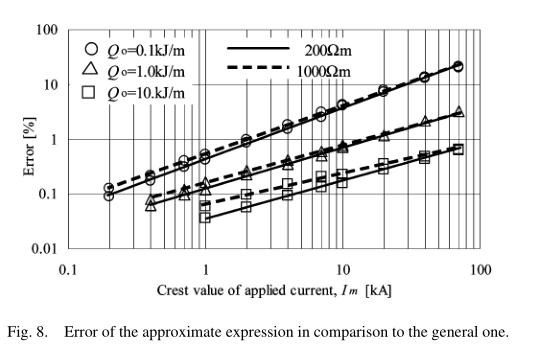
本节通过与一般表达式的比较来考察近似表达式的准确性。图8显示了与图5对应的情况下近似表达式与一般表达式的比较误差。

由图8可知，近似表达式的误差与该近似表达式在小于10ka时具有足够的精度。

6. 结论

本文提出了一种基于土壤电离能平衡的电流相关接地电阻模型。所提出的模型考虑了油化带的增加和区域电阻率的变化，以代表当前的依赖关系。 该模型由能量函数表示。图8。与一般表达式相比，近似表达式的误差。存储在电离区中，并显示出对接地电阻的滞后效应。 已经描述了所提议模型的近似表达式和一般表达式。该模型具有线性特征的物理含义，例如由于土壤电离和去离子作用而引起的电流依赖性和接地电阻的磁滞效应。 该模型已通过与实验结果进行比较进行了验证。

参考文献

[1] P. L. Bellaschi, “Impulse 60-cycle characteristics of driven grounds,” AIEE Trans., vol. 60, pp. 123–128, 1941. [2] P. L. Bellaschi, R. E. Armington, and A. E. Snowdon, “Impulse 60-cycle characteristics of driven grounds,” AIEE Trans., pt. II, vol. 61, pp. 349–363, 1942. [3] A. V. Korsuntcev, “Application of the theory of similitude to the calculation of concentrated earth electrodes,” Electrichestvo, no. 5, pp. 31–35, 1958. [4] A. C. Liew and M. Darveniza, “Dynamic model of impulse characteristicsofconcentratedearth,”Proc.Inst.Elect.Eng.,vol.121,pp.123–135, 1974. [5] E. E. Oettle, “A new general estimation curve for predicting the impulse impedance of concentrated earth electrodes,” IEEE Trans. Power Del., vol. 3, no. 4, pp. 2020–2029, Oct. 1988. [6] A. M. Mousa, “The soil ionization gradient associated with discharge of high currents into concentrated electrodes,” IEEE Trans. Power Del., vol. 9, no. 3, pp. 1669–1677, Jul. 1994. [7] T. Matsui, M. Adachi, H. Fukuzono, S. Sekioka, O. Yamamoto, and T. Hara, “Measurements of grounding resistances of a transmission-line tower base connected with auxiliary grounding electrodes for high impulse currents,” in Proc. 10th Int. Symp. High Voltage Engineering, vol. 5, Montreal, QC, Canada, 1997, pp. 257–260. [8] S. Sekioka, H. Hayashida, T. Hara, and A. Ametani, “Measurements of grounding resistancesforhigh impulsecurrents,” Proc.Inst.Elect. Eng., Gen., Transm. Distrib., vol. 145, no. 6, pp. 693–699, 1998. [9] S. Sekioka, T. Sonoda, and A. Ametani, “Experimental study of currentdependent grounding resistances of rod electrode,” IEEE Trans. Power Del., vol. 20, no. 2, pp. 1569–1576, Apr. 2005. [10] J. M. Prousalidis, M. P. Philippakou, N. D. Hatziargyriou, and B. C. Papadias,“Theeffectofionizationinwindturbinegroundingmodeling,”in Proc. Mediterranean Electrotechnical Conf., Cyprus, 2000, pp. 28–31. [11] M.I.Lorentzou,N.D.Hatziargyriou,andB.C.Papadias,“Time domain analysis of grounding electrodes impulse response,” IEEE Trans. Power Del., vol. 18, no. 2, pp. 517–5124, Apr. 2003. [12] “Perspectives on soil ionization,” in Proc. International Conference on Grounding and Earthing, Belo Horizonte, Brazil, 2000, CIGRE Task Force on Soil Ionization—WG 33.01, pp. 105–106. [13] M. Hayashi, “Observation of streamer in the soil by surge current” (in Japanese), J. Inst. Elect. Eng. Jpn., vol. 87-1, pp. 133–141, 1967. [14] “Guide to Procedures for Estimating the Lightning Performance of Transmission Lines,”, CIGRE Working Group 33.01, 1991. [15] D. P. Snowdon and J. W. Erler, “Initiation of electrical breakdown of soil by water vaporization,” IEEE Trans. Nucl. Sci., vol. 30, no. 6, pp. 4568–4571, Dec. 1983. [16] “Applications of Black Box Modeling to Circuit Breakers,” ELECTRA, no. 139, pp. 40–71, 1993. [17] O. Mayr, “Beitrage zur theorie des statschen und des dynamischen lichtbogens,” Arch. fur Elektrotechnik, vol. 37, pp. 588–608, 1943. [18] A. M. Cassie, “Arc Rupture and Circuit Severity: A New Theory,” CIGRE, Paris, France, Report no. 102, 1939. [19] T. Inaba, “Analytical similarity between stabilized arc characteristics and transport properties in gases” (in Japanese), Trans. Inst. Elect. Eng. Jpn., vol. 94-A, no. 3, pp. 83–90, 1974. [20] A. Ametani, “The application of the fast Fourier transform to electrical transients phenomena,” Int. J. Elect. Eng. Educ., vol. 10, pp. 277–281, 1973.