Principle and design of a single-phase inverter-based grounding system for neutral-to-ground voltage compensation in distribution networks
配电网中性点接地补偿的单相逆变器接地系统原理与设计
Wang W, Yan L, Zeng X, et al. Principle and design of a single-phase inverter-based grounding system for neutral-to-ground voltage compensation in distribution networks[J]. IEEE Transactions on Industrial electronics, 2016, 64(2): 1204-1213.
摘要
由于Petersen线圈与分布电容之间的分布参数不对称和谐振,在无效接地的电源系统中可能会发生中性点对地过电压。 因此,中性点对地电压的约束对于配电网络的安全至关重要。 为此,提出了一种基于单相逆变器的有源接地系统及其控制参数设计方法。 推导了其输出电流与中性点对地电压之间的关系,以解释中性点对地电压补偿的原理。 然后,提出了一种实用的电流检测方法来指定补偿电流的参考。 然后提出了一种由比例谐振(PR)和比例积分(PI)以及电容性电流反馈组成的电流控制方法,以确保在较大的负载变化范围内具有足够的输出电流精度和稳定性裕度。 以PI方法为比较方法,详细介绍了两种控制方法的性能。 实验结果证明了所提出的接地系统和控制方法的有效性和新颖性。
1. 引言
无论从理论上还是实践上,配电网接地系统的主要目的都是限制接地电流以消除由单线接地故障引起的电弧。 但是,通常不考虑接地系统的其他目的,即将中性点到地电压控制在一定范围内[1]。 这对于电力系统的安全至关重要,特别是当固有不对称性很高时。
固有的不对称性直接决定了未接地系统或高电阻接地(HRG)系统中的中性点到地电压[2]。 这是由分布参数的不对称性引起的,即,对地电容和泄漏电阻。 可能导致不对称的原因有很多,包括架空线路中的换位不当,单相或两相开路,中压(MV)单相负载[3]等。而且,中性点对地电压与接地方法。 显然,在有效接地的系统中,它被限制为很小的值。而在谐振接地(RG)系统中,由于Peterson线圈与分布电容之间发生谐振,它甚至可能超过线对中性电压[4]。 为了维护电源的可靠性和消除故障电弧,大多数中压配电网采用HRG或RG方法,这不可避免地产生了中性点对地电压高的问题。
在无效接地的系统中,采取了几种措施来限制中性点到地的电压[3]。 换位增强是架空线降低不对称电压的常用方法。 但是,这种方法需要大量的工作并且实现起来很复杂。 三相耦合电容用于平衡分布电容。 然而,它不足以适应电力系统中操作模式的变化。 RG系统中失谐和阻尼比的提高可以降低由上述谐振引起的中性点对地电压[4]。 但是,这种方法不能消除由于分布参数不对称而引起的中性点对地电压。
为了消除中性点到地的过电压,需要一个有源接地系统,该系统具有向中性点注入某些电流并使它看起来像接地短路的特性。 显然,该系统无法通过电阻,电抗器或电容器之类的无源组件来实现。 因此,本文采用基于单相逆变器的接地系统。
电流检测和控制方法对于逆变器的控制系统至关重要。 这两个方面对于有源接地系统的设计和实施都是巨大的挑战。 关于电流检测方法,文献[5]-[10]介绍了几种充电电流检测方法。 在[5]中,通过两次改变彼得森线圈电感并测量相应的中性点到地电压和彼得森线圈电流来检测分布电容。 然后可以通过测量的参数和线-垂直电压轻松计算出充电电流。 但是,这种方法依赖于彼得森线圈的存在,因此不能在有源接地系统中采用。 文献[7]通过故障馈线的相电压和三相电流的变化介绍了一种充电电流检测方法。 该方法可以通过馈线终端单元轻松实现。 但是,该方法使用了太多的传感器,因此很难保证精度。 在[10]中引入了通过固定电阻和接触器将一相接地的螺栓连接,以检测充电电流。 这种方法可以很容易地保证电流精度。 但是,它仍然需要一个接地电阻,并且检测过程对于有源接地系统的控制来说太复杂了。 另外,由于用于电压补偿的电流与充电电流不同,因此这些方法不能直接用于补偿中性点至地电压。
配电变压器始终处于三角形/星形连接,因此馈线的三相负载对零序阻抗没有影响。 由于零线对地电压仅取决于零序电路,因此接地系统的实际负载就是分布式阻抗。 显然,负载主要是电容性的,并且可能会在基本频率附近与接地系统的LC滤波器发生谐振。 这可能会导致稳态误差并破坏控制系统的稳定性裕度。这些功能使有源接地系统控制器的拓扑和参数设计变得复杂。 已有几篇文献讨论了载荷效应和共振现象,并提出了许多有效措施[11]-[14]。文献[11]提出了一种比例积分微分(PID)和谐振加负载电流反馈的混合控制器,以减少稳态误差并在处理不同负载类型时改善动态响应。然而,没有详细讨论控制器参数的设计。 文献[12]讨论了有源电力滤波器中LCL滤波器的固有不稳定性,并介绍了电容性电流反馈(CCF)的有源阻尼方法以提高稳定性裕度。 降级方法可以简化LCL滤波器控制系统的设计[14]。 但是,由于接地系统的负载类型与LCL滤波器的负载类型不同,因此,未经修改就不能采用这些方法。
本文提出了一种基于单相逆变器的新型接地系统,可以灵活地控制中性点对地电压。 首先推导了接地系统注入电流与中性点对地电压之间的关系。 然后,通过分析这种关系,介绍了一种用于补偿中性点至地电压的实用电流检测方法。 此外,详细讨论了负载效应和共振现象,然后提出了当前的控制策略。 然后提出了控制器设计方法,以满足控制系统的要求。随后提供用于验证所提出的控制拓扑和设计方法的实验结果。
2. 主动接地系统原理
A. 中性点接地电压补偿原理
本文研究了一个带有一个馈线的典型10kV非有效接地配电网[15]。 图1显示了带有本文提出的有源接地系统的配电网络拓扑。 由于10kV母线是通过星形/三角形变压器$T_d$从110kV系统提供的,因此没有实际的中性点。 因此,使用了一个Z/星形变压器$T_z$来接地变压器,并将接地系统连接在该点和地面之间。 图2显示了简化的配电网络,其中$E_A$,$E_B$,$E_C$是三相电压。X相(X = A,B或C)的分布电容和电阻分别为$C_X$和$R_X$。 接地系统由单相全桥逆变器,LC型输出滤波器和耦合变压器$T_i$组成。逆变器的DC总线由一个三相非受控整流器供电,该整流器连接到$T_z$的次级绕组。 系统的输出电流由IGBT的PWM脉冲控制,以执行补偿电流基准检测和中性点至地电压补偿。 变压器用于调节逆变器输出电压,并将逆变器与配电网络隔离。
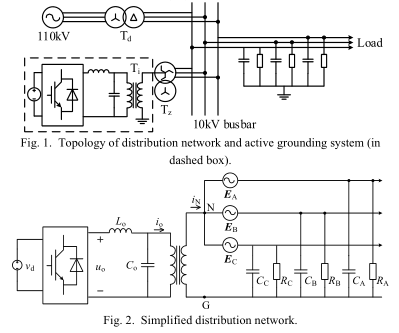
假设逆变器的输出电流完全受控,则可以将接地系统视为理想的电流源。 根据电路理论,配电网的划分可以简化为与阻抗串联的电压源。 因此,整个系统的电路可以简化为图3,其中$E_{eq}$和$G_∑$分别表示配电网的等效电压源和阻抗。 它们由(1)和(2)表达,其中$Y_X$是相对地导纳,即$Y_X =jω_0C_X+ 1 / R_X$,而ω0表示基本角频率。
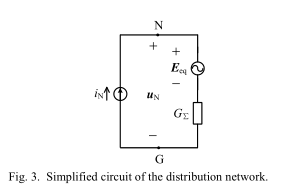
\[E _ { eq } = - G _ { \Sigma } ( E _ { A } Y _ { A } + E _ { B } Y _ { B } + E _ { C } Y _ { C } )\tag{1}\] \[G _ { \Sigma } = \frac { 1 } { Y _ { \Sigma } } = \frac { 1 } { Y _ { A } + Y _ { B } + Y _ { C } }\tag{2}\]一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电压源和电阻的串联组合等效置换,此电压源的激励电压等于一端口的开路电压,电阻等于一端口内全部独立电源置零后的输入电阻。《电路》(邱关源) 当使用戴维南定理简化电路时,最重要的法则是:电压源要短路,电流源要开路。
因此,接地系统$i_N$的输出电流与中性点对地电压$u_N$的关系为
\[u _ { N } = i _ { N } G _ { \Sigma } + E _ { eq } = G _ { \Sigma } ( i _ { N } - E _ { A } Y _ { A } - E _ { B } Y _ { B } - E _ { C } Y _ { C } )\tag{3}\]显然,控制$i_N$可以控制中性点对地电压为0,也就是全补偿。
\[i _ { 0 } = E _ { A } Y _ { A } + E _ { B } Y _ { B } + E _ { C } Y _ { C }\tag{4}\]可以进一步得出结论,当电感器或电阻器并联连接到接地系统时,补偿电流参考也满足(4)。 这表明该接地系统适用于带有HRG和RG接地的配电网络。 然而,由于配电网络的分布式参数很复杂,难以精确检测,因此直接计算$i_0$是不切实际的。
由于线对中性点电压也就是相电势平衡,且正序。所以$E_B$、$E_C$可以用$E_A$进行表示,互差120°。以$E_A$的相角作为启示相角,也就是0°,那么$u_N$可以被写成
\[u _ { N } = G _ { \Sigma } ( i _ { N } e ^ { j \theta } - i _ { 0 } e ^ { j \theta _ { 0 } } )\tag{5}\]欧拉公式 $e ^ { i x } = \operatorname { cos } x + i \operatorname { sin } x$
在式(5)中,$\theta$和$\theta_0$分别表示$i_N$和$i_0$的相角。因此,相对地电压幅值可由下式获得。
\[u _ { N } ( i _ { N } , \theta ) = | G _ { \Sigma } | \sqrt { i _ { N } ^ { 2 } + i _ { 0 } ^ { 2 } - 2 i _ { N } i _ { 0 } \operatorname { cos } ( \theta - \theta _ { 0 } ) }\tag{6}\]对上式取一阶偏微分,获得$u_N$的变化率。
\[\frac { \partial u _ { N } ( i _ { N } , \theta ) } { \partial i _ { N } } = | G _ { \Sigma } | \frac { i _ { N } - i _ { 0 } \operatorname { cos } ( \theta - \theta _ { 0 } ) } { \sqrt { i _ { N } ^ { 2 } + i _ { 0 } ^ { 2 } - 2 i _ { N } i _ { 0 } \operatorname { cos } ( \theta - \theta _ { 0 } ) } }\tag{7}\] \[\frac { \partial u _ { N } ( i _ { N } , \theta ) } { \partial \theta } = | G _ { L } | \frac { i _ { N } i _ { 0 } \operatorname { sin } ( \theta - \theta _ { 0 } ) } { \sqrt { i _ { N } ^ { 2 } + i _ { 0 } ^ { 2 } - 2 i _ { N } i _ { 0 } \operatorname { cos } ( \theta - \theta _ { 0 } ) } }\tag{8}\]从式(4)可以看出,在一个确定结构的配电网下,$i_0$和$\theta_0$是确定的。从式(7)可以看出,当设置$\theta$为固定值$\theta^*$时,$u_N$如式(9)所示。
\[i _ { N } = i _ { 0 } \operatorname { cos } ( \theta ^ { * } - \theta _ { 0 } )\tag{9}\]当$\theta$固定为一个$\theta_0$时,既然微分的本质就是无线接近0的一小段,那么可以近似看作式(7)的左半边为0,那么结论就是式(7)的右半边的分子为0,即可得出式(9)结论。
$u_N$的变化趋势可以在几种不同的情况下进行讨论, 若$- \pi / 2 \leq \theta ^ { * } - \theta _ { 0 } < \pi / 2$,随着$i_N$从0增大到无穷大,$u_N$会先降后升。着意味着$u_N$由一个最小值。当$\pi / 2 \leq \theta ^ { * } - \theta _ { 0 } < 3 \pi / 2$,$u_N$会单调增加,所以,$u_N$也会由一个最小值。
从式(8)可以看出,当设置$i_N$为一个固定值$i^*$时,$u_N$会有另外一个拐点,拐点位置在
\[\theta = \theta_0\tag{10}\]B. 补偿电流检测方法
对比公式(9)和(10)可得得出有趣的结论,公式(9)的拐点由$\theta^*$决定,那么它会由设定值$\theta$决定。然而,公式(10)的拐点由$i_N$决定,那么,无论选择什么样的$i_N$,拐点总会变化。第二,$\theta$必须选择$\theta_0$,确保式(9)的拐点与$i_0$幅值相等,这就是补偿电流。这时,式(10)的拐点值正是$i_0$的相角。这些特性可用用于快速定位$i_0$的幅值和相位。
通过上面的分析,如果将具有任何固定大小和变化相位的正弦电流注入中性线,则$i_0$的相位可以通过探测$u_N$的最小值获得。相应的,只有当注入电流的相位设成$\theta_0$时,$i_0$的幅值可以被顶位,这可以从图4和图5中的矢量图更直接地看到。在这些图中,$u_N$的大小除以$G_∑$的大小用以简化分析。
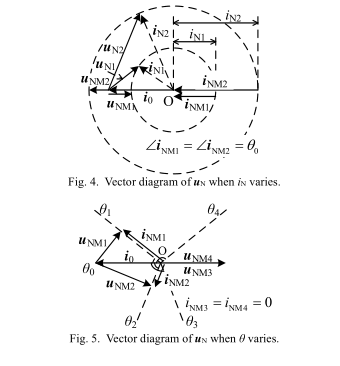
图4显示了不同$i_N$下$u_N$的变化。可以选择两种典型的值,$i_{n1}$和$i_{N2}$,第一个比$i_0$小,第二个比$i_0$大,假设两组$i_N$注入中性点,相应的$u_N$可以被式(5)描述。显然,它们的起始点固定在i0的尾部,并且它们的终点遵循虚线中的圆,如$u_{N1}$和$u_{N2}$所示。根据几何定律,径向矢量在两组中都具有最小的幅度,如$u_{NM1}$和$u_{NM2}$所示。 相应的注入电流矢量由$i_{NM1}$和$i_{NM2}$表示。 显然,它们具有与$θ_0$相同的相角,因此可以得出结论,无论选择多少注入电流幅度,对应于$u_N$最小幅度的电流的相角都与$θ_0$相同。
图5显示了当选择不同的$i_N$相角时$u_N$的变化。 选择$θ_1$至$θ_4$进行比较; 它们中的两个相对于$i_0$的角度差($θ_1$和$θ_2$)的夹角小于π/ 2,其余较大($θ_3$和$θ_4$)。 假设将具有这些相角的四组$i_N$注入中性点,则可以根据(5)绘制相应的$u_N$组。 对于$u_N$的前两组,很明显,当$u_N$垂直于$i_N$时,出现最小量级,如$u_{NM1}$和$u_{NM2}$所示。 与其对应的注入电流矢量分别为$i_{NM1}$和$i_{NM2}$。 对于$i_N$的其他两个角度,最小$u_N$仅在$i_N$变为零时才出现,如$u_{NM3}$和$u_{NM4}$所示。 可以看出,对应于最小$u_N$的电流幅值均不等于$θ_0$。
可以得出结论,当将$i_N$的大小预设并固定到足够大的值以进行精确检测时,可以通过检测最小的$u_N$来确定$i_0$的角度。 反之,如果将$i_N$的角度预设并固定为某个值,则通过检测最小的$u_N$很难确定$i_0$的大小。因此,可以画出检测$i_0$的幅值和相位的简便方法。
首先,将$i_N$的大小预设为一定值; 通过改变$i_N$的角度并将其注入中性点来搜索$u_N$的最小量; 对应于最小$u_N$的相位角为$θ_r$。 然后,将$i_N$的角度固定为$θ_r$; 通过改变iN的大小并将其注入中性点来再次搜索$u_N$的最小大小; 相应的幅度即为$i_r$。 最后,用于补偿配电网不对称性的当前参考值是$i_r$的大小和$θ_r$的角度。
3. 电流控制策略
A. 控制模型
由于线间电压很少变化,因此在控制分析期间我们将其视为零。 因此,可以将图3中的电压源$E_{eq}$视为短路。 通过将等效阻抗$G_∑$转换为$C_S$和$R_S$到耦合变压器的转换器侧,主电路因此简化为图6。
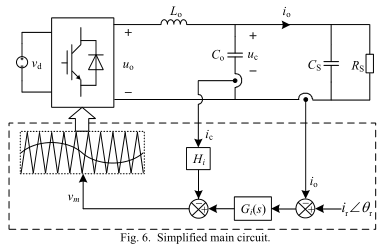
在进行电流控制时,一种典型的方法是使用输出电流反馈。 图7显示了系统的反馈控制图,其中$Δi_0$是输出电流误差。从该图可以看出,调制信号$v_m$与逆变器输出电流$i_0$之间的关系由$G_1$表示。
\[G _ { 1 } ( s ) = \frac { i _ { 0 } ( s ) } { v _ { m } ( s ) } = \frac { K _ { pwm } ( s R _ { s } C _ { s } + 1 ) } { s ^ { 2 } R _ { s } L _ { 0 } ( C _ { o } + C _ { s } ) + s L _ { o } + R _ { s } }\tag{11}\]通常将LC滤波器的电感$L_o$设置为较小,当频率达到$ω_r$时会发生谐振。
\[\omega _ { r } = \sqrt { \frac { 1 } { L _ { 0 } ( C _ { 0 } + C _ { s } ) } }\tag{12}\]图8显示了$G_1$的Bode图,表1中列出了典型参数。配电网络的参数与具有50A充电电流的实际参数相同。 在图8中,可以明显地看到$ω_r$的共振。 该谐振使$G_1$相移。 谐振频率与$C_s$有关,$C_s$随配电网络参数而变化。如果频率落在低频段,则稳态误差会增加。
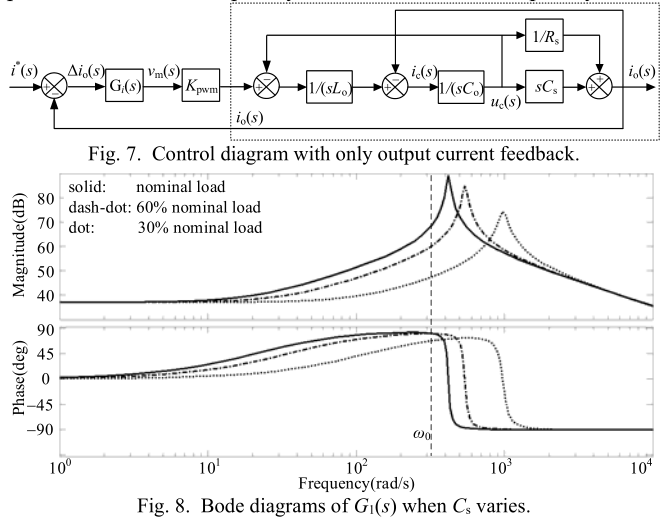

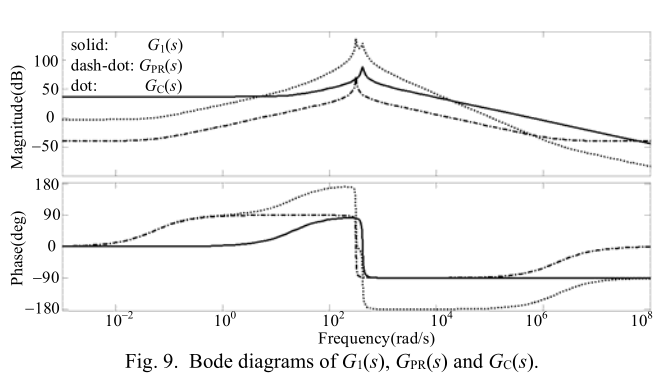
图8还显示了随着$C_s$标称值,标称值的60%和30%变化的伯德图。随着$C_s$的减小,基本角频率的幅度从67.7 dB减小到47.1 dB,这意味着在基本频率处稳态误差显着增加。此外,如果谐振频率位于中频带,则控制系统的相位裕度可能会降低。 为了保证基频的最小稳态误差,通常采用比例谐振控制器[16]。 但是,如图9中的伯德图所示,控制器也会带来-180°相移。 由于交叉频率$ω_c$始终处于中频带,可能大于$ω_r$和$ω_0$,因此整个控制系统的相位裕度$G_C(s)= G_{PR}(s)G_1(s)$接近零,这使得系统很容易不稳定。
B. 电容电流反馈
根据以上分析,应仔细抑制共振,以满足控制性能要求[17]-[19]。本文提出了一种主动阻尼方法,该方法可以灵活地阻尼共振,而不会造成任何损失,如图10所示。在这种方法中,$C_0$的电流以$H_i$的比率反馈到控制回路。 因此,从电流调节器输出$v_r$到输出电流$i_0$的传递函数为
\[G _ { 2 } ( s ) = \frac { i _ { o } ( s ) } { v _ { r } ( s ) } = \frac { K _ { pwm } ( s R _ { s } C _ { s } + 1 ) } { s ^ { 2 } R _ { s } L _ { o } ( C _ { o } + C _ { s } ) + s ( L _ { o } + K _ { pwm } H _ { i } R _ { s } C _ { o } ) + R _ { s } }\tag{13}\]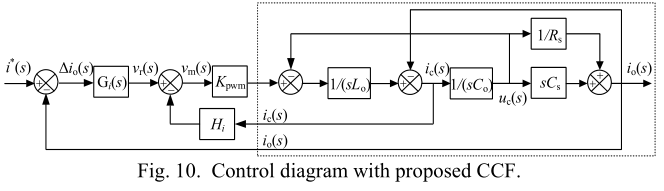
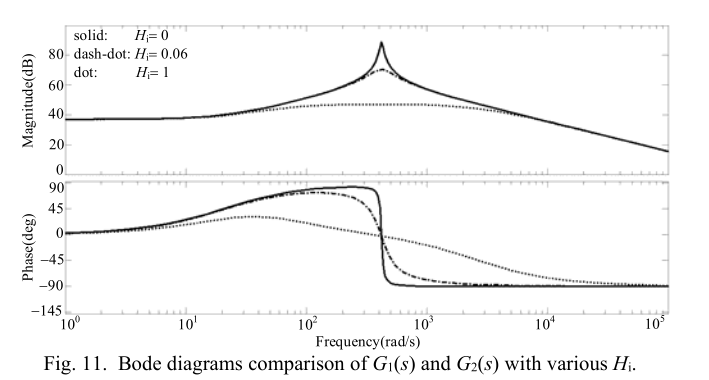
显然,电容性电流反馈(CCF)引入了$K_{pwm}H_iR_sC_o$与分母s项的比值。 结果,$G_2$的大小在原始谐振频率$ω_r$处显着减小,这有效地抑制了控制系统。 图11显示了原始系统和阻尼系统的Bode图。 显然,CCF会衰减谐振频率下的幅度,并增强系统的相位裕度。 阻尼度随着反馈比Hi的增加而增加,这意味着谐振频率的幅度较小,相位裕量较大。同时,CCF在基频处也带来较小的幅度,破坏稳态性能。 因此,电流调节器必须在基频处具有很大的幅度,以实现最小的稳态误差。
C. 电流调节器
电流调节器采用阻尼形式的PR控制器,以增强稳态性能并适应电力系统的频率变化。
\[G _ { PR } ( s ) = k _ { p _ { - } PR } + \frac { 2 k _ { r } \omega _ { i } S } { s ^ { 2 } + 2 \omega _ { i } S + \omega _ { 0 } ^ { 2 } }\tag{14}\]在低频带和高频带中,PR控制器的大小仅由比例比$k_{p_PR}$确定。 为了避免高阶谐波干扰,整个控制系统的交叉频率始终设置在中频带,通常为开关频率的1/10 [20]。 为了满足此要求,$k_{p_PR}$不应太大。 但是,受限的$k_{p_PR}$可能无法确保系统稳定性,如稍后所示。 因此,PR控制器几乎不能同时满足抗干扰和控制系统稳定性的要求。 因此,引入了附加的PI控制器。
\[G _ { PI } ( s ) = k _ { p _ { - } PI } + \frac { k _ { i } } { s }\tag{15}\]复合控制器的优点是零频率时增益无限大,高频时增益固定。 因此,容易在低频带上扩大系统增益并避免其对交叉频率的影响。 还应仔细选择积分比$k_i$,以防止低频的-90◦相移破坏相位裕量。因此,整个系统的电流调节器和开环传递函数可以描述如下。
\[G _ { i } ( s ) = G _ { PR } ( s ) G _ { PI } ( s )\tag{16}\] \[G _ { t } ( s ) = G _ { PR } ( s ) G _ { PI } ( s ) G _ { 2 } ( s )\tag{17}\]4. 控制参数设计
A. PWM 约束
首先描述PWM约束,以便可以在以下分析中使用该结论。 为了实现可实现的脉冲宽度调制,调制波形在一个开关周期内仅应与载波波形交叉一次。 也就是说,调制波形的最大频率不应超过开关频率[21]。因此,以下表达式成立。
\[H _ { i } \leq \frac { 4 f _ { sw } L _ { o } } { K _ { pwm } }\tag{18}\]B. PI控制器
由于PI控制器在低频段具有-90◦相移,这可能会降低控制系统的相位裕度,因此控制器的转折频率应远小于交叉频率。 那是
\[\frac { k _ { i } } { k _ { p _{ —PI} } } \ll \omega _ { c }\tag{19}\]可以调整比例比例$k_p{PI}$以略微改变整个系统的性能。 为了简化参数设计,将$kp_PI$设置为1,因此在中频及以上频段,PI控制器的影响可忽略不计。 因此,下面的积分比表示成立。
\[k _ { i } \ll \omega _ { c }\tag{20}\]C. 交叉频率$\omega_c$
为了防止PR控制器的相移减小相位裕量,交叉频率$ω_c$始终设置为远离基频的中频带。因此,PR控制器可以简化为以比例比确定的分频频率下的纯放大器环路。 如上所述,可以将交叉频率处的PI控制器视为具有$kp_PI$增益的比例环路。 因此,电流控制器在交叉频率处的增益为
\[| G _ { i } ( j \omega _ { c } ) | = | G _ { PR } ( j \omega _ { c } ) G _ { PI } ( j \omega _ { c } ) | = k _ { p _ { - } PR }\tag{21}\]由于交叉频率处的开环增益的大小为1,因此可以通过以下公式获得$ω_c$,$k_p_{PR}$和$H_i$的关系。
\[| G _ { t } ( j \omega _ { c } ) | = 1\tag{22}\]使用(13)至(21),可以得出以下等式。
\[| \frac { k _ { p , PR } K _ { pwm } ( 1 + j \omega _ { c } R _ { s } C _ { s } ) } { R _ { s } [ 1 - \omega _ { c } ^ { 2 } L _ { 0 } ( C _ { o } + C _ { s } ) ] + j \omega _ { c } ( L _ { o } + K _ { pwm } H _ { i } R _ { s } C _ { o } ) } | = 1\tag{23}\]请注意,配电网的阻尼比$d = 1 /(ω_0R_sC_s)$的典型值为0.03至0.08。 与一个相比,它可以忽略不计。 LC滤波器$C_0$的电容总是被设置为比分布电容$C_s$小得多。 因此,可以将(23)重写为
\[| \frac { k _ { p _ { DR } } ( 1 - j d \frac { \omega _ { 0 } } { \omega _ { c } } ) } { \frac { d \omega _ { 0 } L _ { o } } { K _ { pwm } } + H _ { i } \frac { C _ { o } } { C _ { s } } - j \frac { 1 } { K _ { pwm } } ( \frac { 1 } { \omega _ { c } C _ { s } } - \omega _ { c } L _ { o } ) } | = 1\tag{24}\]考虑到Cs在分频频率下的电抗远小于$L_0$的电抗,因此,(24)可以进一步简化为
\[k _ { p _ { - } PR } ^ { 2 } - H _ { i } ^ { 2 } ( \frac { C _ { o } } { C _ { s } } ) ^ { 2 } = ( \frac { \omega _ { c } L _ { o } } { K _ { pwm } } ) ^ { 2 }\tag{25}\]从(18)可以看出,$H_i$被限制为较小的值。此外,$C_0$远小于$C_s$,因此以下表达式成立。
\[k _ { p _ { - } PR } = \frac { \omega _ { c } L _ { o } } { K _ { pwm } }\tag{26}\]由于$G_2(s)$的零频增益为(13)的$K_{pwm} / R_s$,如果使用具有一定比例比(26)的单个PR控制器,则整个系统在零频时的增益为
\[\frac { \omega _ { c } L _ { o } } { K _ { pwm } } \frac { K _ { pwm } } { R _ { s } } = \frac { \omega _ { c } L _ { o } } { R _ { s } }\tag{27}\]通过表1中列出的典型值,可以看出$ω_c L_0 / R_s$小于1。 因此,具有单个PR控制器的零频率控制系统的增益低于0 dB线,这意味着整个控制系统在某种程度上处于不稳定状态,如图12所示。它还显示了添加PI控制器后的稳定控制系统。
D. 稳态误差和稳定裕度约束
基频下输出电流误差的大小用于描述稳态误差。
\[E _ { i } = | \frac { i ^ { * } ( j \omega _ { 0 } ) - i _ { o } ( j \omega _ { 0 } ) } { i ^ { * } ( j \omega _ { 0 } ) } | \tag{28}\]假设施加了输出电流的单位反馈,则上式可以用开环传递函数来描述
\[E _ { i } = | 1 - \frac { G _ { t } ( j \omega _ { 0 } ) } { 1 + G _ { t } ( j \omega _ { 0 } ) } | = | \frac { 1 } { 1 + G _ { t } ( j \omega _ { 0 } ) } | \tag{29}\]由于PR控制器的幅度在基频处为$k_{p_PR} + k_r$,因此使用式(13)至(17),可以将(29)转换为
\[\frac { 1 } { E _ { i } } = | 1 + \frac { ( k _ { p _ { - } PR } + k _ { r } ) K _ { pwm } } { d \omega _ { 0 } L _ { o } + K _ { pwm } H _ { i } C _ { o } / C _ { s } - j ( 1 / \omega _ { 0 } C _ { s } - \omega _ { 0 } L _ { o } ) } | \tag{30}\]在基频,$L_0$的电抗可以忽略不计。此外,与$k_{p_PR} + kr$相比,$H_iC_0 / C_s$可以忽略不计。 为了简化分析,也忽略了基频$C_s$的电抗。 结果,稳态误差约束可以描述为
\[\frac { k _ { p _ { LR } } + k _ { r } } { H _ { i } } \approx \frac { C _ { o } } { C _ { s } E _ { i } } \tag{31}\]显然,电流控制器在基频处的增益与稳态误差成反比。增加增益可以获得更好的稳态性能。但是,CCF比值$H_i$与误差成正比,即意味着更好的负载共振阻尼会带来更大的稳态误差。
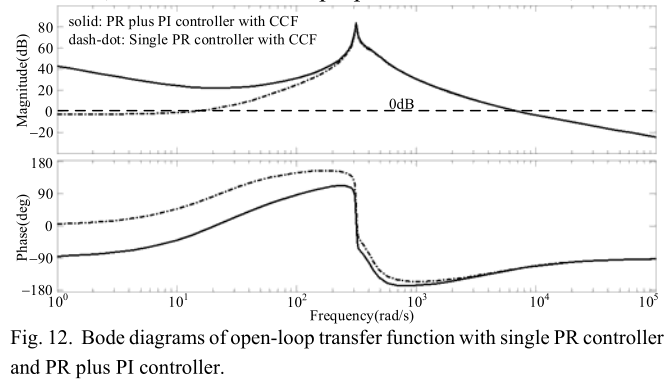
从图12中可以看出,通过仔细选择控制器参数,开环传递函数的相位将不会超过-180◦线。 这些选择技巧包括:PI控制器的转折频率应远离分频频率,并且PR控制器的谐振截止频率应尽可能小。因此,可以实现无限的增益裕度。
在处理相位裕量约束时,有必要考虑谐振比对相移的影响。 考虑交叉频率下的PR控制器,
\[G _ { PR } ( j \omega _ { c } ) = k _ { p _ { - } PR } + 2 k _ { r } \omega _ { i } / s \tag{32}\]如上所述,可以将PI控制器视为交叉频率处的纯放大器环路。 因此,相位裕度(PM)可以表示如下。
\[P M = 180 ^ { \circ } + \angle G _ { PR } ( j \omega _ { c } ) + \angle G _ { 2 } ( j \omega _ { c } ) \tag{33}\]使用(13)和(32),考虑到$C_s$在交叉频率下的电抗可以忽略不计,在附录中推导了相位裕度的约束,并表示如下。
\[\frac { k _ { r } } { k _ { p _ { p _ { PR } } } } \geq \frac { \omega _ { c } ( \omega _ { c } L _ { o } C _ { s } + K _ { pwm } C _ { o } H _ { i } \operatorname { tan } P M ) } { 2 \omega _ { i } ( \omega _ { c } L _ { o } C _ { s } \operatorname { tan } P M - K _ { pwm } C _ { o } H _ { i } ) } \tag{34}\]5. 参数设计及实验结果
为了验证理论分析,对PI和PR以及带或不带CCF的PI(复合控制器)的两种控制方法进行了比较研究。 由于在实验结果中不容易观察到稳定裕度,因此使用伯德图进行说明。 实验分析着重于动态和稳态性能。
A. 参数设计
根据理论分析,PI和PR控制器的参数受表达式(20),(26),(31)和(34)约束。 因此,需要设置交叉频率,稳态误差和相位裕度。
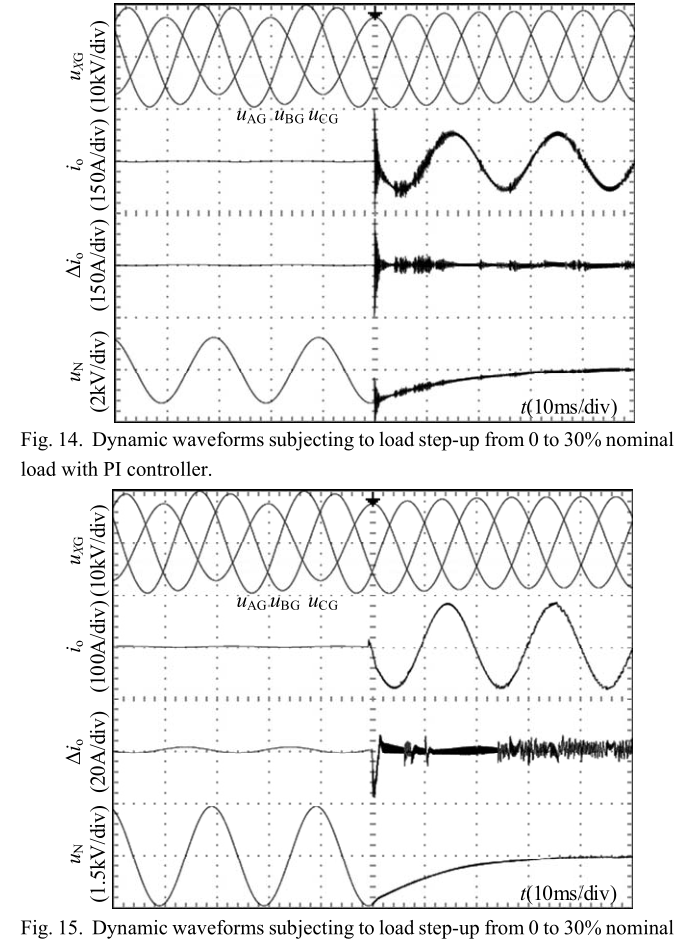
由于开关频率固定为10 kHz,因此交叉频率设置为1 kHz。 稳态误差设置为0.5%,以保证良好的稳态性能。 相位裕度设置为60°,以确保足够的稳定性裕度。 PI控制器的转折频率设置为30 Hz,以避免干扰稳态精度和稳定性裕度。 因此,可以如表II所示获得两个控制器的参数。 调节后的开环传递函数的伯德图如图13所示。可以看出,控制系统的交叉频率为7.13×103 rad / s,略高于设定值。基频增益为83.3 dB,这意味着稳态误差为6.45×10-5,远小于设定值。 这是因为谐振率kr不仅由稳态误差约束表达式(31)确定,而且还由PM约束表达式(34)确定。 在此选择较大的kr即可满足这两个要求。 开环功能的相位不超过-180◦线,这表明增益裕量是无限的。 此外,相位裕度为61.3°,接近设定值。
PI和复合控制器的比较Bode图也显示在图13中,两者都没有CCF。 显然,前者具有更大的分频频率和相位裕度,比拟议的具有更快的响应和更好的稳定性。 但是,它不能有效地抑制输出电流的谐波。 没有CCF的复合控制器遭受负载谐振的the180°相移,因此由于负增益裕量而不稳定。建议的接地系统的额定电压和额定电流也需要讨论。 从系统拓扑结构来看,额定电压与(1)和(2)中所示的中性点到地电压有关。 接地系统的补偿电流由分布参数的不对称性确定,如(4)所示。 从这些表达式可以看出,最坏的情况发生在两相开路条件下。 在这种情况下,中性点电压上升到线对中性点电压,并且补偿后的电流基准达到系统充电电流的1/3。
B. 实验结果
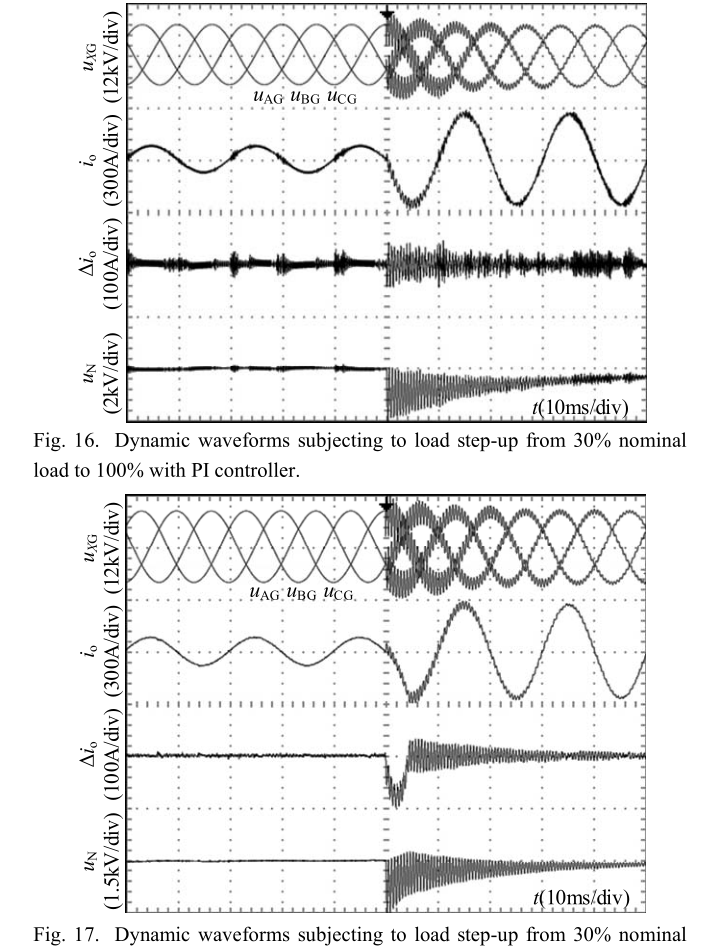
为了在实践中验证提议的有源接地系统,在实验室中根据图1中的拓扑和表I中的参数构建了一个100kVA的原型。对拓扑进行了细微的更改,即使用了升压变压器来转换电源。 将380V电源供应到10kV,用110kV电源和变压器Td代替。 接地系统的逆变器主要由两个来自英飞凌的并联单相IPM模块FF450R12ME4组成。 耦合变压器Ti的容量为100kVA。 固有的相对地电容和电阻是通过两组与标称值相对应的电容器和电阻器实现的,表I中的最大功率值和其中的30%代表两个不同的负载水平。 上面讨论的控制方法在载波信号频率为10 kHz的数字信号处理器TMS320F28335开发平台中执行。 在实验过程中,首先将负载从0%提升到30%额定负载,然后再将负载从30%提升到100%。 不带CCF的PI控制器被作为与建议的带CCF的复合控制器的比较控制器。 输出电流的参考值通过第二节中提出的补偿电流检测方法进行检测。 在图14至图17中示出了利用不同的控制器经受两次升压的动态波形。为了清楚地观察控制性能,示出了输出电流Δio(见图7)的误差。
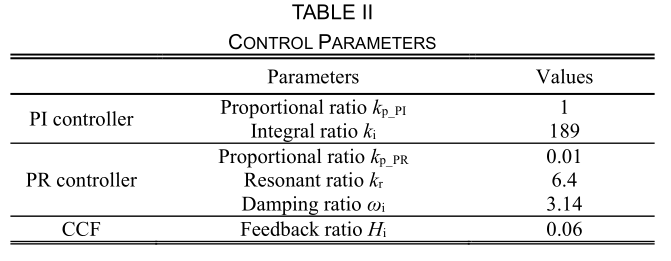
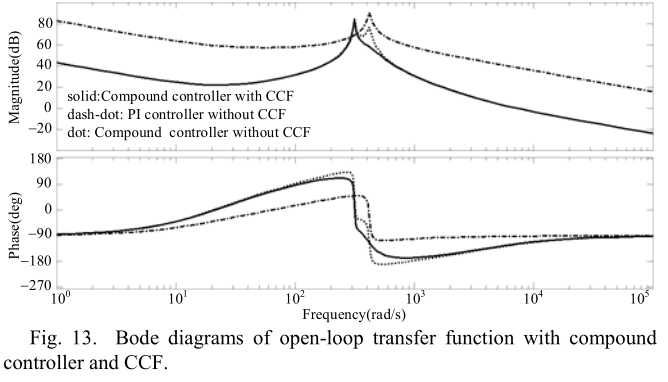
从输出电流的动态波形可以看出,两种方法都可以达到稳定的系统输出。 由于PI控制系统的带宽较大,因此PI控制器的调整时间略短于所建议的方法,如图13所示。但是,图14和图15表明PI方法的过冲比所建议的方法大。 几乎是输出电流和中性点到地电压的两倍,这对电源设备的安全性有害。 从图16可以看出,采用PI方法,在100%额定负载下输出电流的百分比误差小于30%的额定负载,这可以通过第三节中的负载效应来解释。
相比之下,如图17所示,与PI方法相比,所提出的控制器在负载变化前后的输出电流百分比误差相对更小,这表明所提出的控制器比PI控制器更适合负载变化。 应当注意的是,由于负载的时间常数较大,因此负载变化后中性点到地电压的动态过程比输出电流的动态过程要长。
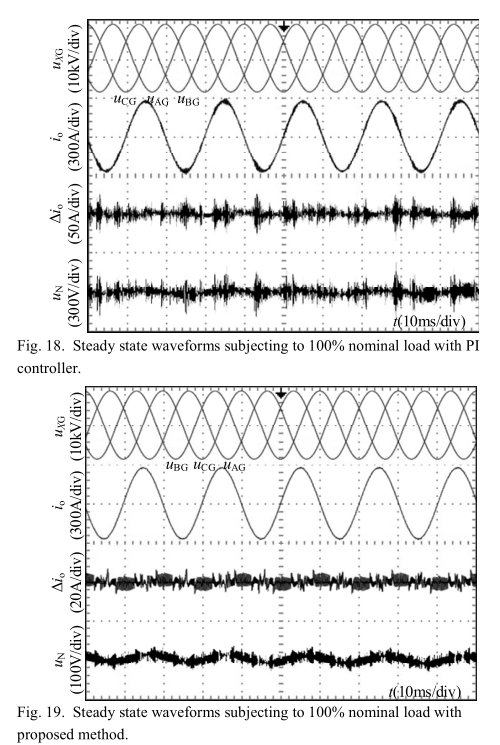
图18和图19显示了两种控制方法在100%标称负载下的稳态波形。 与所提出的方法相比,使用PI控制器可以观察到输出电流误差和中性点到地电压的基本分量中的误差更大。 频谱分析表明,采用该方法的中性点到地电压主要包含谐波,该谐波具有开关频率的整数倍。 根据PI方法,图18中的中性点至地电压波形显示约42V的降低电压。 频谱分析表明,输出电流的总谐波失真(THD)为5.1%。 从图19的输出电流和电流误差波形可以看出,该方法的稳态误差达到3%。所提出的方法通过接地系统将中性点对地电压降低到21V左右,优于PI方法。 所提方法的输出电流的总谐波失真达到3.0%,也优于PI方法。 中性点对地电压和输出电流THD均表明该方法比PI方法具有更好的稳态性能。
6. 结论
所提出的有源接地系统能够有效地约束中性点至地的电压,以避免由于不对称的分布参数或Petersen线圈与相地电容之间的谐振而引起的可能的过电压。 提出了一种实用的补偿电流检测方法,该方法首先确定相角,然后确定电流基准的大小。 还提出了一种电流控制方法,该方法由PR加PI控制器和电容性电流反馈组成。 所提出的控制方法适用于大范围的负载变化,并且不受负载电容与输出LC滤波器电感之间可能产生谐振的影响。 实验结果表明,所提出的控制方法在动态和稳态下的性能均优于PI方法。
附录
在此推导出$kr / kp_PR$约束的相位裕量(PM)限制。$G_2(jɷc)$的表达式可以很容易地从(13)中获得。 将分母和分母除以$jω_cR_sC_s$,并考虑$C_0 « C_s$并用d代替$1 /(ω_0R_sC_s)$,得出
\[G _ { 2 } ( j \omega _ { c } ) = \frac { K _ { pwm } ( 1 - j d \frac { \omega _ { 0 } } { \omega _ { c } } ) } { \frac { L _ { o } + K _ { pwm } H _ { i } R _ { s } C _ { o } } { R _ { s } C _ { s } } + j ( \omega _ { c } L _ { o } - \frac { 1 } { \omega _ { c } C _ { s } } ) } \tag{A.1}\]由于$C_s$在分频频率下的电抗比$L_0$小得多,并且$d_{ω0}/ω_c« 1$,(A.1)可以重写为
\[\angle G _ { 2 } ( j \omega _ { c } ) = - \operatorname { arctan } \frac { \omega _ { c } L _ { o } R _ { s } C _ { s } } { L _ { o } + K _ { pwm } H _ { i } R _ { s } C _ { o } } \tag{A.2}\]使用(A.2)和(32),(33)可以重写为
\[P M = 180 ^ { \circ } - \operatorname { arctan } \frac { 2 k _ { r } \omega _ { i } } { k _ { p _ { PRR } } \omega _ { c } } - \operatorname { arctan } \frac { \omega _ { c } L _ { o } R _ { s } C _ { s } } { L _ { o } + K _ { pwm } H _ { i } R _ { s } C _ { o } } \tag{A.3}\]等式(A.3)可以用不等式重写为
\[\operatorname { rctan } \frac { 2 k _ { r } \omega _ { i } } { k _ { p , PR } \omega _ { c } } + \operatorname { arctan } \frac { \omega _ { c } L _ { o } R _ { s } C _ { s } } { K _ { pwm } H _ { i } R _ { s } C _ { o } } > 180 ^ { \circ } - PM \tag{A.4}\]将切线函数运算应用于(A.4)的两侧,可获得以下表达式。
\[\frac { k _ { r } } { k _ { p _ { pR } } } \geq \frac { \omega _ { c } ( \omega _ { c } L _ { o } C _ { s } + K _ { pwm } C _ { o } H _ { i } \operatorname { tan } P M ) } { 2 \omega _ { i } ( \omega _ { c } L _ { o } C _ { s } \operatorname { tan } P M - K _ { pwm } C _ { o } H _ { i } ) } \tag{A.5}\]参考文献
[1] IEEE Recommended Practice for Grounding of Industrial and Commercial Power Systems, IEEE Std. 142-2007, 2007.
[2] L. J. Kingrey, R. D. Painter, and A. S. Locker, “Applying High-Resistance Neutral Grounding in Medium-Voltage Systems,” IEEE Trans. Ind. App., vol. 47, no. 3, pp. 1220– 1231, May 2011.
[3] X. Zeng, Y. Xu, and Y. Wang, “Some novel techniques for insulation parameters measurement and Petersen-coil control in distribution networks,” IEEE Trans. Ind. Electron., vol. 57, no. 4, pp. 1445–1451, Apr.2010.
[4] A. Kalyuzhny, “Analysis of Temporary Overvoltages During Open-Phase Faults in Distribution Networks With Resonant Grounding,” IEEE Trans.Power Del., vol.30, no.1, pp.420-427, Feb. 2015.
[5] X. Lin, J. Huang, and S. Ke, “Faulty Feeder Detection and Fault SelfExtinguishing by Adaptive Petersen Coil Control,” IEEE Trans. Power Del., vol.26, no.2, pp.1290-1291, Apr. 2011.
[6] M. Brenna, E. D. Berardinis, L. D. Carpini, P. Paulon, P. Petroni, G. Sapienza, G. Scrosati, and D. Zaninelli, “Petersen Coil Regulators Analysis Using a Real-Time Digital Simulator,” IEEE Trans. Power Del., vol.26, no.3, pp.1479-1488, July 2011.
[7] X. Zeng, K. K. Li, W. L. Chan, S. Su, and Y. Wang, “Ground-Fault Feeder Detection With Fault-Current and Fault-Resistance Measurement in Mine Power Systems,” IEEE Trans. Ind. App., vol. 44, no. 2, pp. 424– 429, Mar.2008.
[8] J. Tian, Q. Chen, L. Cheng, and Y. Zhang, “Arc-suppression coil based on transformer with controlled load,” IET Elect. Power App., vol.5, no.8, pp.644-653, September 2011.
[9] X. Chen, B. Chen, C. Tian, J. Yuan, and Y. Liu, “Modeling and Harmonic Optimization of a Two-Stage Saturable Magnetically Controlled Reactor for an Arc Suppression Coil,” IEEE Trans. Ind. Electron., vol.59, no.7, pp.2824-2831, July 2012
[10] D. Paul, P. E. Sutherland, and S. A. R. Panetta, “A Novel Method of Measuring Inherent Power System Charging Current,” IEEE Trans. Ind.App., vol. 47, no. 6, pp. 3230– 3240, Nov. 2011.
[11] D. Dong, T. Thacker, R. Burgos, F. Wang, and D. Boroyevich, “On zero steady-state error voltage control of single-phase PWM inverters with different load types,” IEEE Trans. Power Electron., vol. 26, no. 11, pp.3285– 3297, Nov. 2011.
[12] Y. Tang, P. C. Loh, P. Wang, F. H. Choo, F. Gao, and F. Blaabjerg, “Generalized design of high performance shunt active power filter with output LCL filter,” IEEE Trans. Ind. Electron., vol. 59, no. 3, pp. 1443– 1452, Mar. 2012.
[13] F. Liu, Y. Zhou, S. Duan, J. Yin, B. Liu, and F. Liu, “Parameter Design of a Two-Current-Loop Controller Used in a Grid-Connected Inverter System With LCL Filter,” IEEE Trans. Ind. Electron., vol. 56, no. 11, pp.4483–4491, Nov. 2009.
[14] G. Shen, X. Zhu, J. Zhang, and D. Xu, “A New Feedback Method for PR Current Control of LCL-Filter-Based Grid-Connected Inverter,” IEEE Trans. Ind. Electron., vol. 57, no. 6, pp. 2033–2041, Jun. 2010.
[15] X. Dong and S. Shi, “Identifying Single-Phase-to-Ground Fault Feeder in Neutral Noneffectively Grounded Distribution System Using Wavelet Transform,” IEEE Trans. Power Del., vol. 23, no. 4, pp. 1829-1837, Oct.2008.
[16] A. Kuperman, “Proportional-Resonant Current Controllers Design Based on Desired Transient Performance,” IEEE Trans. Power Electron., vol.30, no. 10, pp. 5341–5345, Oct. 2015.
[17] R. Peña-Alzola, M. Liserre, F. Blaabjerg, R. Sebastián, J. Dannehl, and F. W. Fuchs, “Analysis of the Passive Damping Losses in LCL-Filter-Based Grid Converters,” IEEE Trans. Power Electron., vol. 28, no. 6, pp. 2642– 2646, Jun. 2013.
[18] W. Wu, Y. He, T. Tang, and F. Blaabjerg, “A New Design Method for the Passive Damped LCL and LLCL Filter-Based Single-Phase Grid-Tied Inverter,” IEEE Trans. Ind. Electron., vol. 60, no. 10, pp. 4339–4350, Oct.2013.
[19] M. Liserre, R. Teodorescu, and F. Blaabjerg, “Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values,” IEEE Trans. Power Electron., vol. 21, no. 1, pp. 263– 272, Jan. 2006.
[20] Erickson and D. Maksimovic, Fundamentals of Power Electronics, 2nd ed. Norwell, MA, USA: Kluwer, 2001, pp. 331–408.
[21] C. Bao, X. Ruan, X. Wang, W. Li, D. Pan, and K. Weng, “Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping,” IEEE Trans. Power Electron., vol. 29, no. 3, pp. 1239 - 1253, Mar. 2014.