摘要

由于土壤离子化，在高脉冲电流下接地电极的有效半径变得大于电极的外径。因此，接地脉冲阻抗不同于通常在小电流下测量的60 Hz接地电阻。如果已知土壤的临界电场，则可以估算任何给定脉冲电流的脉冲阻抗。因此，对于接地系统设计以及雷电性能研究，必须有一个广义的土壤临界电场方程。这里提出了土壤临界电场$E_c$的广义方程，它是土壤介电常数$k_g$和电导率$\sigma_g$的函数。在不同的土壤，不同的水分含量下进行了广泛的脉冲测试和电气测量。介电常数k g通过使用土壤填充的同轴传输线的波传播技术测量。统计分析了波形对不同土壤临界电场$E_c$的影响。

1. 简介

先前的研究人员已经提出，如果已知土壤E c的临界电场，则可以准确估算接地棒的脉冲阻抗[1,2]。然而，先前的研究报道了各种各样的E c值（70-2700 kV / m）[3-7]。 Oettle [4]建议E c值为1 MV / m。但是，Mousa [6]观察到Oettle的结果在600–1850 kV / m的范围内变化，对于水分含量较高的土壤，其值较低（600–800 kV / m）。 Mousa进一步观察到，在雷暴天气和野外条件下，不均匀度要比实验室条件下高得多，Oettle结果的下限约为一半，即300-400 kV / m。 MousacitedLiew和Dayveniza [3]成功地使用临界电压为300 kV / m来模拟观察到的多个电极的动态行为。因此，Mousa建议将300 kV / m用于典型土壤的临界电场。

由于土壤的电学特性因一种土壤类型而异，因此，$E_c$的单一值是不合理的。因此，必须有适用于任何土壤类型的临界电场$E_c$的广义方程。

土壤的电参数是土壤电阻率$\rho_g$，介电常数$\varepsilon_g$（$\varepsilon_g = k_g \varepsilon_0$）和渗透率（$\mu_g = \mu_0 \mu_r$），其中空气中的$\mu_0$介电常数$varepsilon_0 = 8.854 \times 10^{-12}F/m$和$\mu_0 = 4 \pi \times 10^{-7}H/m$。除非土壤中没有任何磁性材料，否则参数$\mu_g = \mu_0$。据报道，频域测量土壤和岩石的介电常数和电阻率会随测量频率和水分含量的变化而显着变化[8-10]。据报道，电容随着频率的增加呈指数下降。电容测量中的误差是由极化效应引起的，极化效应与频率有关。但是，由于脉冲电压或电流是时间相关的现象，因此接地系统的脉冲行为也是时间相关的现象。因此，在时域内测量土壤电参数似乎更为合适。

这项研究的目的是根据不同类型土壤的广泛实验室测试结果，根据重要土壤参数$k_g$和$\sigma_g$提出土壤临界电场的广义表达式（$E_c$模型）。统计分析了各种土壤中波形对临界电场$E_c$的重要性。

2. 实验

在田纳西理工大学的电磁瞬态实验室中进行了土壤电学特性（$E_c,\rho_g,k_g$）的实验研究，提出了土壤临界电场的广义方程。有田纳西州六个不同地区的土壤。从初步测试中选择了三种土壤，它们的电特性差异最大。

2.1 土壤准备

实验室测试中的土壤样品是均匀的土壤，没有石块，砾石，木屑和其他异物。将所需量的土壤保存在浅盘中，并在烤箱中于约115°C的温度下干燥至少48小时。然后将充满土壤的托盘在室温下冷却，用铝箔包裹，以防止水分从大气中进入。然后加入去离子水，并与给定重量的土壤混合以达到规定的水分含量。水分含量是土壤中的水分含量占土壤干重的百分比。制备过程已在[1]中描述。

2.2 测量土壤电特性

在实验室中针对三种不同的土壤类型测量了土壤电参数。对于每种土壤类型，在四个含水量（5、10、15和20％）下随机设计三个重复项，并具有三个不同的波形（0.1 / 50、1.2 / 50和5/50 ms），以避免测量偏差。

2.2.1 土壤电阻率

使用带有两个圆形板的顶部和底部电极的充满土壤的圆柱体作为测试设备（图1）。圆柱体由内径为10厘米（$d$），高度为1厘米（$l$）的Schedule 40 PVC管制成。两个电极都是直径为13厘米，厚度为4毫米的圆形316 L不锈钢板。这种设置在两个不锈钢圆盘电极之间的土壤中产生均匀的电场。此设置用于土壤电阻测量和脉冲测试。

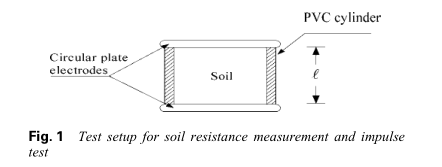
通用无线电桥模型1656用于测量土壤阻力。由土壤电阻R的测量值计算土壤电阻率$\rho_g$和电导率$\sigma_g$为

$\rho _ { g } = \frac { R a } { \ell } = \frac { 1 } { \sigma _ { g } } ( \Omega m ) \tag{1}$

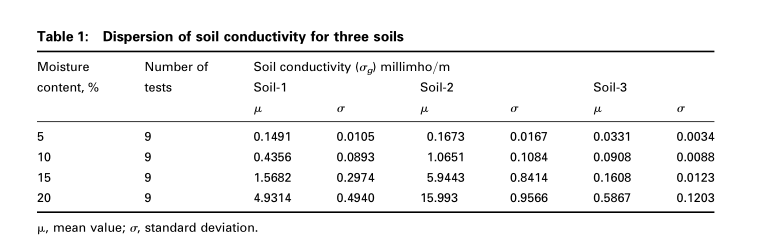
其中，R是测试对象的交流电阻（以V为单位），a是测试对象的横截面积，以$m^2$为单位，$l$是两个电极之间的距离（以m为单位）。表1中显示了三种土壤在四种不同水分含量下的电导率的平均值和标准偏差。每种水分含量的测试总数为9，其中包括每组测试的三次重复以及三种不同的测试所施加的脉冲电压的波形。

2.2.2 土壤介电常数

设计了一条同轴传输线，图2a，在远端短接，用于通过波传播方法测量土壤介电常数$k_g$。该同轴传输线连接到测试电路，如图3所示。50 V同轴电缆由DC电压源充电。通过合上水银开关，可以将充满电的同轴电缆的电压完全释放到充满污垢的同轴圆筒上。使用示波器来测量脉冲电压。测试电路的所有连接均使用50 V同轴电缆完成，示波器输入端通过50 V电阻器端接。这样做是为了防止测试电路反射。土壤的制备方法与土壤电导率的测定方法相同。

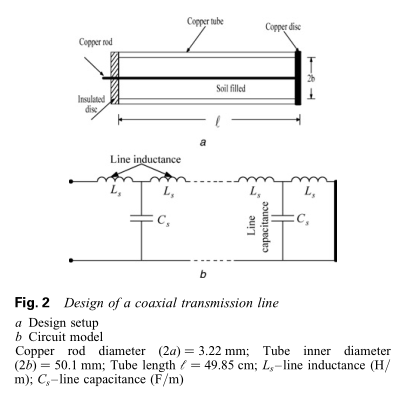
图4a显示了在50 V负载下带电同轴电缆的矩形脉冲电压。矩形脉冲电压的持续时间取决于同轴电缆的长度和穿过同轴电缆的波速。图4b示出了充满土壤的同轴圆柱体两端的电压。穿过充满土壤的圆柱体的正向波从短路端以反极性反射。这又减小了在带电同轴电缆中产生的矩形脉冲的宽度。电压脉冲的持续时间（$X_1 - X_2$），即“往返”传播时间，取决于圆柱体长度和传播波的速度。

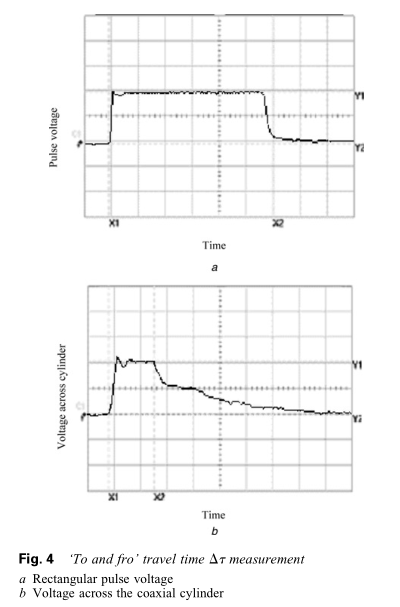
传输线上的波$v_c$的速度计算为

$v _ { c } = \frac { 2 \ell } { \Delta \tau } = \frac { 1 } { \sqrt { L _ { s } C _ { s } } } = \frac { 1 } { \sqrt { L _ { s } ( C _ { 0 } k _ { g } ) } } = \frac { c } { \sqrt { k _ { g } } } \tag{2}$

土壤介电常数$k_g$计算为

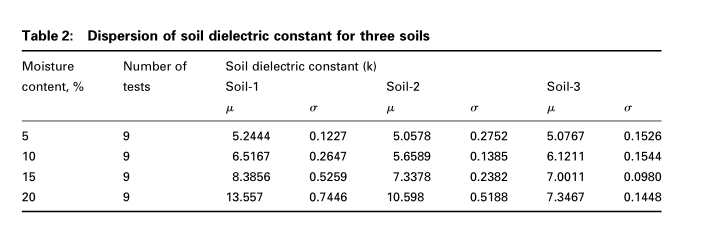
其中$l$是传输线的长度（以m为单位），$\Delta \tau$是“往返”通过该线的时间（以s为单位），$C_0（F / m）$是该线在空气中的电容，$L_s（H / m）$是线的电感，c是自由空间中的光速（$3 \times 10^8 m / s$）。表2列出了这三种土壤的介电常数的平均值和标准偏差。

2.2.3 均匀电场下的土壤临界电场$E_c$

由四级400 kV脉冲发生器进行脉冲测试，以确定均匀场设置下测试对象的耐压和击穿电压（图1）。三种不同的冲击电压波形（0.1 / 50、1.2 / 50和5/50 ms）应用于测试对象。脉冲测试从脉冲发生器的低充电电压开始。充电电压以1 kV的步长增加，直到发生击穿为止。击穿后，充电电压从击穿水平降低1 kV，直至测试对象承受施加的电压。测试至少进行了五次连续测试（耐压和击穿电压）。五组的平均值被视为对特定土壤样品的一项观察。用电阻分压器测量输出电压。电压信号由四通道500 MHz数字示波器记录，并存储在个人计算机中。

由土壤击穿之前的耐压计算土壤临界电场$E_c$

$E _ { c } = \frac { V _ { \text { withstand } } } { \ell } ( kV / m ) \tag{4}$

其中$V _ { \text { withstand }}$承受力是土壤被击穿之前测试对象上的电压（以kV为单位），$l$是测试对象的高度（以m为单位）。

3. 结论

3.1 波形对土壤临界电场$E_c$的意义

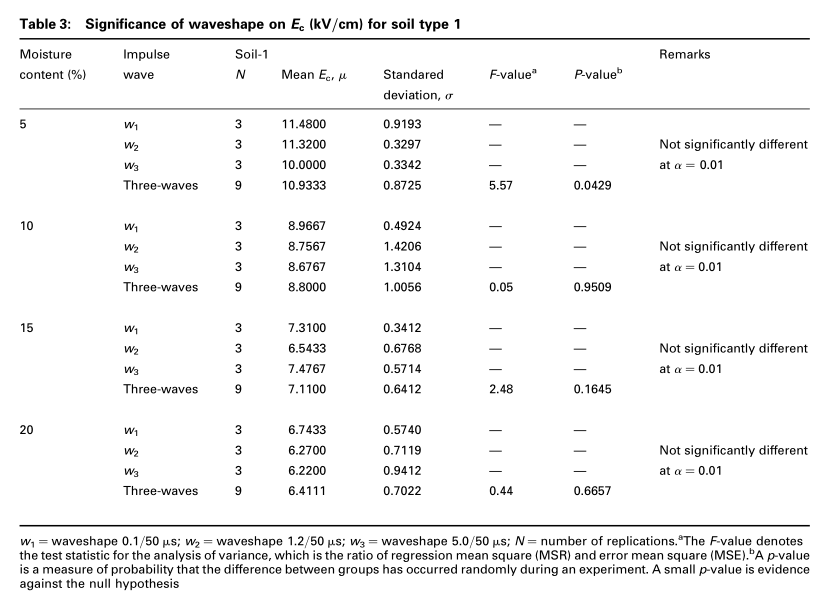
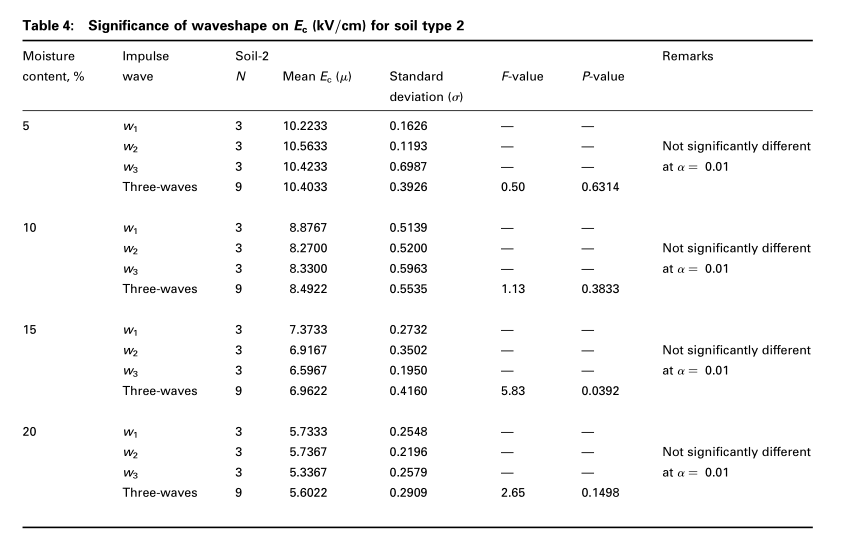
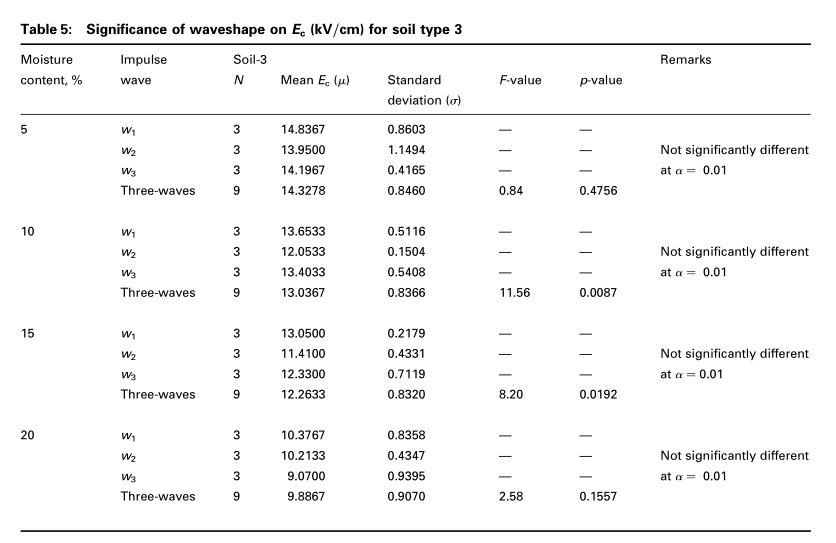
考虑了三种波形的脉冲电压（$w_1 = 0.1/50, w_2 = 1.2/50,w_3 = 5/50ms$），以确定波形对临界电场$E_c$的影响。用SAS软件统计分析了波形对$E_c$的重要性。在显着性水平上执行单向ANOVA，在三种不同土壤的三种波形中，每种水分含量的$\alpha = 0.01$。从方差分析中可以明显看出，波形的影响对土壤临界电场$E_c$没有显着影响，如表3-5所示。

3.2 $E_c$与$\sigma_g$以及$E_c$与$k_g$之间的关系

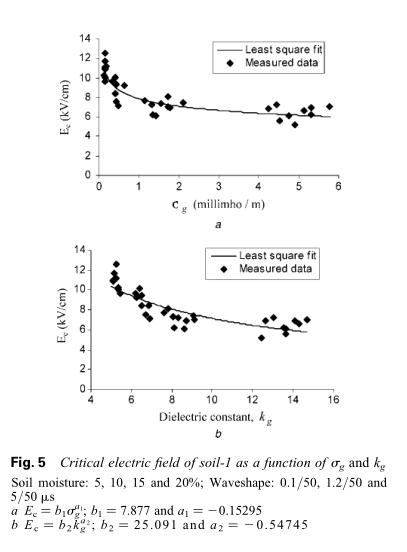
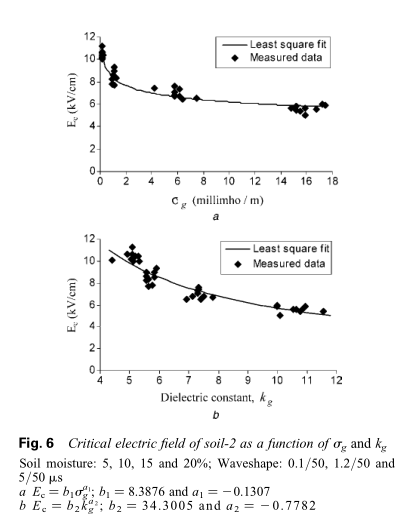
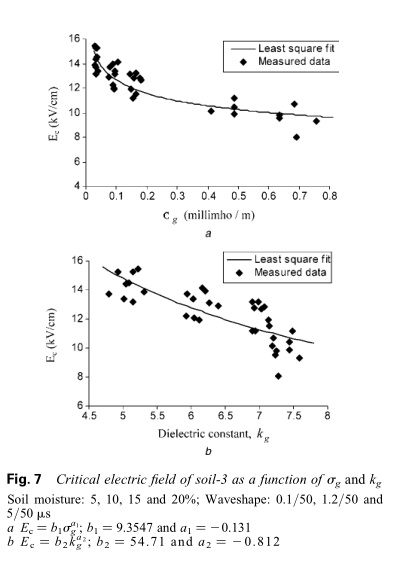
最小二乘拟合法用于找到给定一组测量数据点的最佳拟合关系。图5-7显示了三种不同土壤的$E_c$与$\sigma_g$以及$E_c$与$k_g$之间的关系。该关系可被描述为：$E _ { c } = b _ { 1 } \sigma _ { g } ^ { a _ { 1 } }$和$E _ { c } = b _ { 2 } k _ { g } ^ { a _ { 2 } }$，其中a 1，a 2，b 1和b 2是特定土壤的常数。

从图5-7可以看出，三种土壤的$E_c$与$\sigma_g$以及$E_c$与$k_g$之间的关系完全不同，因为它们的as和bs值不同。

在$\alpha = 0.01$处的方差分析表明，四种含水量下三种土壤之间的土壤临界电场$E_c$显着不同。显然，土壤电导率$\sigma_g$和介电常数$k_g$这两个参数都受土壤水分含量的影响，而$E_c$取决于土壤电导率$\sigma_g$和介电常数$k_g$。

3.3 土壤分解的物理解释

土壤是一种复合结构，由充满空气和水，溶解的矿物质和有机物质的颗粒和空隙组成。土壤的分解是由将空气困在土壤颗粒周围的空隙中。空隙和土壤颗粒是两种单独的介质，起着混合电介质的作用。两种介质之间的界面处的法向位移向量相等。可以将空隙中产生的电场$E_1$计算为

$E _ { 1 } = \frac { \varepsilon _ { 2 } } { \varepsilon _ { 1 } } E _ { 2 } \tag{5}$

其中$\varepsilon_1$和$\varepsilon_2$分别是空隙率（对于空气，$\varepsilon_1 = \varepsilon_0$）和土壤颗粒的介电常数，$E_2$是土壤颗粒中的电场。由于$\varepsilon_2 > \varepsilon_1$，在空隙中产生的电场将更大（即$E_1 > E_2$），从而引起土壤分解。

空隙和土壤颗粒的电阻路径充当电阻分压器。最初施加的大部分电压都出现在空隙上，因为空隙的电阻高于土壤颗粒的电阻。一旦空隙中的电压超过击穿水平，总电压就会出现在土壤颗粒上并发生击穿。

因此，土壤介电常数$k_g$和电导率$\sigma_g$都是引起土壤电击穿的重要参数。

应当记住，改变土壤水分含量会同时改变土壤介电常数$k_g$和电导率$\sigma_g$。换句话说，在图5-7中，土壤介电常数$k_g$和电导率$\sigma_g$均变化。虽然在图5a，6a和7a中，$E_c$的变化相对于$\sigma_g$作图，$E_c$的变化也会受$k_g$的变化的影响。类似地，在图5b，6b和7b中也一样。需要确定$E_c$与$\sigma_g$和$k_g$的显式关系。

3.4 提出$E_c$模型

对土壤电参数的推论测试（ANOVA）和对土壤击穿现象的物理解释表明，土壤介电常数$k_g$和电导率$\sigma_g$都是导致土壤电击穿的重要参数。多元回归使用对数转换变量（$\sigma_g$，$k_g$和$E_c$）作为模型[11]

$\operatorname { log } E _ { c } = \beta _ { 0 } + \beta _ { 1 } * \operatorname { log } k _ { g } + \beta _ { 2 } * \operatorname { log } \sigma _ { g } + \varepsilon _ { i } \tag{6}$

其中

其中$E_c$是响应变量，$\sigma_g$，$k_g$是预测变量，$\varepsilon _ { i }$是误差项，即$E_c$的实际对数值与拟合对数值之间的差。

通过回归分析，提出了土壤临界电场$E_c（kV / cm）$的预测模型。

$E _ { c } = 8.6083 * ( k _ { g } ) ^ { - 0.0103 } * ( \sigma _ { g } ) ^ { - 0.1526 } \tag{7}$

其中，$k_g$是土壤介电常数，$\sigma_g$是土壤电导率（单位为毫米/米）。图8显示了适用于任何土壤类型的预测土壤临界电场$E_c$作为$\sigma_g$和$k_g$的函数的3-D图。图中108个测试点与相应估计点之间的$E_c$有效值差为8.94％。

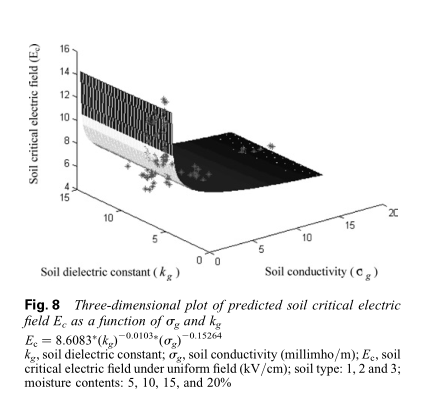
应注意图8和5b，6b和7b中，$k_g$有显著区别。在图5b-7b中，关系式$E _ { c } = b _ { 2 } k _ { g } ^ { a _ { 2 } }$假定土壤电导率是恒定的，但实际上并非如此。 $\sigma_g$和$k_g$的影响分别包含在式（7）和图8中。

## 3.5 土壤样品的多重分解

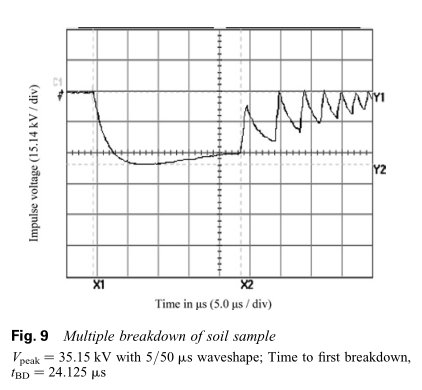
在脉冲测试期间，由于土壤电离效应，在峰值脉冲电压和击穿瞬间之间观察到时间滞后。在临界击穿电压的水平上，大多数土壤样品的击穿发生时间为5-25 ms。但是，在施加电压5/50 ms时，观察到了多次土壤击穿（图9）。在脉冲发生器最后一级的输出端串联一个高电阻，以产生5/50 ms的波。首先，在触发脉冲之后，立即有小电流流过土壤样品，直到土壤样品上的电压幅度达到击穿水平。在击穿过程中，由于穿过击穿路径的土壤中出现了大量电子，导致流过土壤样品的电流大小变得非常大，从而导致串联电阻两端出现高压降。由于这个原因，土壤样品两端的电压水平立即崩溃，土壤样品中的电弧变得不稳定并试图冷却。电弧熄灭后，土壤样品上的电压再次增加。一系列的电压崩溃和上升发生在整个土壤样品上，直到发生器电路中的电容器完全放电，从而导致多次土壤击穿，如图9所示。

# 4. 结论

1.土壤的介电常数k g可以通过波传播技术使用充满土壤的同轴传输线来测量，这消除了极化效应。这是一种创新方法。

2.施加的脉冲电压的波形对土壤临界电场$E_c$没有明显影响。

3.土壤临界电场的新的广义方程$E _ { c } = 8.6083 ^ { * } ( k _ { g } ) ^ { - 0.0103 * } ( \sigma _ { g } ) ^ { - 0.1526 } ( kV / cm )$，是在考虑大量土壤参数的广泛实验室测试基础上提出的，适用于任何土壤条件。

4.可以通过将$E_c$模型纳入接地系统动态模型中来估算脉冲阻抗，这是合理而准确的。