土壤冲激特性的动力学模型
Dynamic model of impulse characteristics of concentrated earths
ps:所有的从动杆或驱动杆的意思都是接地极
摘要
建立了描述多个集中土非线性电涌电流特性的动力学模型。 该模型在电阻率范围从5000 Ω cm到31000 Ω cm的土壤中,不时准确地解释了这些地球的浪涌行为。 与以前描述它们的方法相比,这带来了显着的改进。 使用新模型研究高雷电流下的集中地时,可以预料到比以前假设更大的电涌减小因子。 这项研究旨在克服以前从微不足道的实验结果中推断出值的困难。
符号说明
$R_E$接地电阻 $V$地电阻电压 $I$入地电流 $\rho$土壤电阻率 Ωcm $\rho_0$低电流下的土壤电阻率 Ωcm $g_c$击穿电压梯度 kV/cm $J$电流密度 $kA/cm^{-2}$ $J_c$击穿电流密度 $kA/cm^{-2}$ $r$单元半径 $r_{cm}$最大临界半径 $r_c$临界击穿半径 $d_r$外壳厚度 $r_0$从动杆半径 $l$从动杆深度 $d$从动杆之间的分离 $R_s$电泳发生器的串联电阻 $L_s$电泳发生器的串联电抗 $C$电泳发生器的电容 $V_0$电泳发生器的输出开路电压 $B$电流密度能力指数 $\tau_1$电离时间常数 $\tau_2$去电离时间常数
1. 简介
屏蔽线的雷电反击率对塔-地连接的电阻非常敏感。 1浪涌减小因子通常在2到3之间,以解决在高浪涌电流下观察到的电阻减小(与低交流电测试获得的值相比)。 通常用于确定合适的降低因子的基本数据是Bellaschi,2,3 Berger 4和Davis and Johnson,5,他们对各种土壤和电极配置进行了浪涌测试,电流高达12 kA。 但是,这样的电流幅度远远小于能够引起反向闪络的电流-对于设计良好的线路,通常大于50 kA。 通过微不足道的实验结果外推确定在如此高的雷电电流下的值不可避免地会导致误差和不确定性。 在动态行波类型计算中,6进一步需要电流和时变(动态)表示的塔基阻力。 考虑到该参数在预测计算中的重要性,表明需要一个分析模型来描述观察到的特征。
2. 实验
在昆士兰大学高压实验室进行了一系列实验测试,他们的目的仅限于为开发和验证所提出的模型提供可靠的数据。 选择了三种土壤类型,并在表1中给出了简要说明及其电阻率。土壤电阻率是使用Dwight’s公式根据几个标准电极的低ac电阻测得的。 7土壤A是高压实验室附近的现有土壤,而土壤B和C是专门获得的,并被填充并压实到地面上最初存在土壤A的开挖的2 * 24 m直径的半球形孔中。 表2列出了所用浪涌电流发生器的参数。 峰值电流在1-20 kA范围内变化,波形在6-16和18-54 us范围内,实际值取决于测试对象的特性。 在以下电极上进行了不同充电电压水平的测试:
(a)将直径12’7毫米的杆驱动0. 61 m(2ft)进入土壤 (b)将直径25’4毫米的杆驱动0.61 m(2ft)进入土壤(使用土壤A时,将电极驱动1.83 m) (c)埋在土壤表面的直径152.4 mm的半球形电极 (d)产生火花连接; 通过放置在土壤表面上方的直径为12 * 7毫米的杆进行模拟。

在测试过程中,通过示波器测量并记录了测试接地连接上的脉冲电流和电压。 对于每种土壤,还进行了添加水分和盐溶液以降低电阻率的测试,详细结果在参考文献8中进行了描述。实验测试旨在为验证分析模型提供可靠的数据,而不是详尽的 研究接地连接的浪涌特性。 因此,对后者的讨论将保持在最低限度。
在测试过程中仔细检查了记录的电压和电流波形图,发现单次电涌期间地球行为具有以下特征:
(a)非线性电压/电流特性 (b)电压波的峰值出现在电流峰值之前 (c)最小电阻的瞬间出现在电流峰值之后 (d)在电阻/电流中观察到明显的磁滞效应 (e)当电流降至零时,可以看到特性曲线。
在许多方面,这些特征与Bellaschi等人报道的特征相似,但迄今为止,尚未尝试使用任何分析模型来描述“动态”行为。 特别地,从未分析地再现明显的磁滞特性。
给出更全面的描述如下: (i)土壤A:h.v.附近的“天然”土壤。 实验室; 被归类为砂性轻质粘土,粘土含量约为35%。 土壤的pH值为6’3。存在一些有机物质。 (ii)土壤B:细颗粒和粗颗粒(直径0’02毫米至2毫米)和河砾石(直径2’至5厘米)的50:50混合物。 土壤的pH为8.8。 (iii)土壤C:含中粒砂的壤土砂,大约由以下材料组成: 7%黏土(0.002毫米直径) 10%淤泥(0.002-0.02毫米直径) 83%沙(0.02- 直径2毫米) pH为5.8,并且存在有机物质。
3. 提出动态模型
显然,任何用于描述接地电阻浪涌特性的模型都必须重现观察到的时变磁滞以及土壤中电离效应的破坏。
3.1 动态模型中的基本假设
(a)土壤是均质的和各向同性的; 即在所有方向上的电阻率都相同。
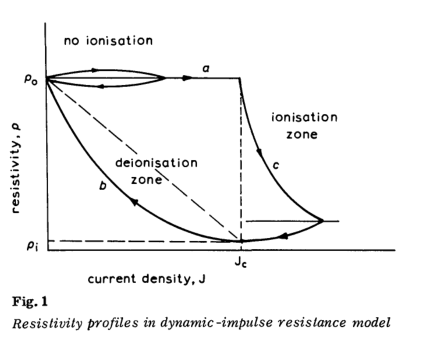
(b)随着电流累积并渗透到土壤中,电流密度大于临界值的区域的电阻率将小于低电流值$\rho_0$。 这对应于击穿,并假定是由于电离增加而随时间变化的扩散生长而发生的。 电阻率从$\rho_0$的较高值到$\rho$的较低状态应具有随时间变化或衰减的时间依赖性
$\rho = \rho _ { 0 } \operatorname { exp } \frac { - t } { \tau _ { 1 } }$
其中$\tau_1$是电流累积时的电离时间常数,t是从电离开始测量的时间。
(c)随着电流的减小,电阻率应以与时间呈指数关系并且与电流密度成指数关系的方式恢复到其原始值$\rho_0$。 前者是一个名词
$( 1 - \operatorname { exp } \frac { - t } { \tau _ { 2 } } )$
其中$\tau_2$是去电离时间常数,t是从衰减瞬间开始测量的时间。 后者由一个术语解释
$( 1 - \frac { J } { J _ { C } } ) ^ { B }$
其中,J是土壤的电流密度,J c是土壤的临界电流密度,B是要确定的指数。 后一个术语包括在能源方面。 电流波的尾部越长,或向土壤中注入的能量越多,电阻率将保持较低的时间越长。 选择指数为2,与能量类型因子一致。 图1显示了随着电流上升和下降的电阻率曲线。
3.2 单从动杆电阻的计算
3.2.1 单根驱动杆的交流线性电阻
半径$r_0$和深度$l$的单个从动杆的电阻已由Dwight通过平均电势方法确定。 但是,考虑一种替代方法,其中假定的等电势模式如图2所示,而不是Dwight假定的等势模式。 对于假定的均匀厚度dr的元素,此假设可产生一个可简单计算的等电位表面积,从而可以在电离开始时定义临界电流密度区域。
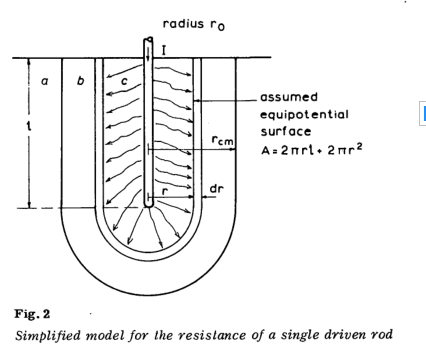
元素壳的电阻由下式给出
$dR = \frac { \rho d r } { 2 \pi ( r ^ { 2 } + r \ell ) } = \frac { \rho dr } { 2 \pi \ell } ( \frac { 1 } { r } - \frac { 1 } { r + \ell } )$
绝缘从动杆的总电阻是通过将从杆表面到无穷大的所有此类元素求和得到的,
$\left. \begin{array}{l}{ R = \int _ { r _ { 0 } } ^ { \infty } \frac { \rho } { 2 \pi \ell } ( \frac { 1 } { r } - \frac { 1 } { r + \ell } ) d }\{ = \frac { \rho } { 2 \pi \ell } ( \operatorname { ln } \frac { r + \ell } { r } ) _ { \infty } ^ { r _ { 0 } } }\end{array} \right.$
当$r \rightarrow \infty , \operatorname { ln } \frac { r + \ell } { r } \rightarrow \operatorname { ln } 1 = 0$
因此
$R = \frac { \rho } { 2 \pi \ell } \operatorname { ln } \frac { r _ { 0 } + \ell } { r _ { 0 } }\tag{1}$
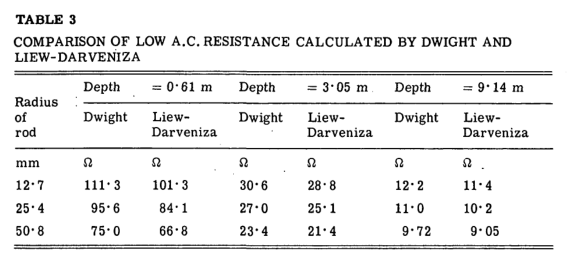
上述表达式表示单个从动杆的线性电阻较低,并且可以与表3中所示的Dwight表达式进行比较。
Dwight 方程:
$R = \frac { \rho } { 2 \pi \ell } ( \operatorname { ln } \frac { 4 \ell } { r _ { 0 } } - 1 )$
Liew-Darveniza方程:
$R = \frac { \rho } { 2 \pi \ell } \operatorname { ln } \frac { r _ { 0 } + \ell } { r _ { 0 } }$
土壤电阻率,$\rho_0 = 10000 \Omega cm$
这两个公式对于驱动各种深度的各种半径的杆比较合理。 差异归因于所使用的近似值。 因此,用于获得等式的近似值。 公式一的精度被认为是令人满意的。
通过使用圆形等电位的相同近似值,可以得出两个和四个对称从动杆的电阻以及直接火花连接的电阻,这些电阻如附录9.1所示。 同样,这些方程式的比较适用于低交流电。 德怀特公式的线性电阻产生令人满意的一致性。
3.2.2 单从动杆的抗冲击性
现在,按照所建议的动力学模型中的假设来计算单个从动杆的抗冲击性。 当向土壤中注入大电流浪涌时,会发生击穿现象,并且一些基本关系如下:
电流密度
$J = \frac { I } { 2 \pi r ^ { 2 } }\tag{2}$
跨元件电压
$ \text{Voltage across element} = \frac { \text { I } \rho dr } { 2 \pi r ^ { 2 } } \tag{3}$
当发生电离击穿时
$\frac { I \rho _ { 0 } dr } { 2 \pi r ^ { 2 } } > g _ { c } dr \tag{4}$
临界电流密度
$J _ { c } = \frac { g _ { c } } { \rho _ { 0 } }\tag{5}$
为了评估瞬时冲击电阻,每个元素的考虑如下:当电流上升并渗透到大地时:
(a)电阻率在$\rho_0$处保持恒定,直到元件的电流密度超过临界值为止
$\rho = \rho _ { 0 } \text { for } J < J _ { C }$
(b)对于超过临界值的电流密度,电阻率以指数方式衰减,对应于土壤中的电离
$\rho = \rho _ { 0 } \operatorname { exp } \frac { - t } { \tau _ { 1 } } \text { for } J \geq J _ { C }$
这样的电离将发生直到达到所获得的电流的峰值的半径$r_{c m}$为止。
随着电流从其峰值衰减,考虑了三个区域(图2):
(i)区域a,其中$r > r_{c m}$和$J < J_c$。 该区域对应于没有被完全电离。 因此
$\rho = \rho _ { 0 } \tag{6}$
(ii)b区,其中$r < r_{c m}$和$J < J_c$。 现在,电流密度J低于临界值,土壤电阻率通过以下方式恢复:
$\rho = \rho _ { i } + ( \sigma _ { 0 } - \rho _ { i } ) ( 1 - \operatorname { exp } \frac { - t } { \tau _ { 2 } } ) ( 1 - \frac { J } { J _ { C } } ) ^ { 2 } \tag{7}$
其中$\tau_2$是去离子时间常数,$p_i$是电阻率的值,其中$J =J_c$电流衰减时,t是从去离子开始测量的时间。
(iii)c区域,其中$r < r_{c m}$和$J \geq J_c$。 电流密度J仍超过临界值,并且电离继续:
$\rho = \rho _ { 0 } \operatorname { exp } \frac { - t } { \tau _ { 1 } } \tag{8}$
这将持续到点$J = J_c$进入区域b为止。
由于对于特定的电流或时间值,每个元素壳都具有不同的电流密度,因此$r_{cm}$内的每个元素必须具有不同的电阻率。 任何时候的总电阻都可以通过将各种电离状态下的壳的元素电阻相加得出。 用数字计算机可以很方便地完成这样的计算。
3.3 确定模型参数$g_c$,$\tau_1$和$\tau_2$
在所提出的模型中,每种土壤的接地连接具有三个参数:$g_c$,$\tau_1$和$\tau_2$。 Bellaschi,3提出了几种土壤的临界梯度$g_c$的值,也可以通过实验确定。 为了确定所使用的三个土壤样品的这些常数,可以求助于开发和使用能够再现实验结果的计算方法。 附录9中提供了一种在电涌电流发生器的C,L和R电路中包括接地电阻表示的方法。2.开发了一个计算机程序来评估所得的非线性电路方程,并产生瞬时电压,电流 以及每个施加电涌的阻力。 最初将$g_c$,$\tau_1$和$\tau_2$的值视为可调变量。 选择它们的值以获得最适合特定浪涌电流的值。 然后将这些选定的值一致地用于预测不同实验条件下土壤的行为,例如: 更大或更小的电流。 但是,对于不同的电极配置,甚至对于相同的土壤,也必须重新校准击穿梯度$g_c$。 这与Petropolous [9]的结果相符,其中通过在平滑电极上添加尖峰来故意降低$g_c$。