Modelling of Dielectric Strength in Long Air Gaps – Application to a complex geometry
摘要
本文对大气隙中正放电的研究提出了新的贡献。 提出了一个模型,可以使用由 Beroual 教授的小组开发的用于长时间正负放电的电路模型来确定非标准几何中的电压 U50 和 k 因子。 该模型基于等效电路图,其参数根据前导通道特性和放电的几何/形态随时间变化。 前导的传播基于与其头部电场计算相关的标准,并考虑了放电路径的随机性。 正如文献中发现的大多数模型一样,该模型仅适用于点平面型电极间隙。 本文由两部分组成:(1)第一部分,介绍了如何将所提出的模型扩展到复杂的几何形状,例如杆-杆电极的间隙; (2) 第二部分介绍了我们对杆平面和杆几何结构进行的实验测试。 实验结果,特别是 U50 和 k 因子的值与从我们的模型推导出的模拟结果进行了比较,对于两种类型的电压波形:雷电脉冲形状和开关脉冲形状(准确地说是临界脉冲形状)。
1. 引言
上个世纪,人们对流光和先导的形成、先导在大气隙中的传播和击穿以及整个放电现象中涉及的物理化学过程进行了大量的实验和理论研究[1-3]。 由于工业上遇到的问题通常涉及介电强度问题,因此大部分工作都集中在最不利的电极几何形状的性能上,也就是说,导致最快间隙击穿的一种是杆面间隙。
在杆平面间隙为正的情况下,电场矢量从杆朝向平面,在尖端附近称为发散场。 从理论的角度来看,这种类型的几何由于其绕点平面轴旋转对称且表征简单,因此具有一定的优势,它只需要两个参数:杆曲率半径和杆面距离 .
为了利用实验数据,建模已成为最合适的工具。 它既可以更好地理解研究配置中的相关参数,也可以对问题提供更详细的响应。 从巴黎经验模型(1967)[4],对实验结果的解析表达式的简单调整,到不再有任何经验公式的物理模型[5, 6],我们遇到了各种各样的模型[7, 6, 8]。
当今可用的最复杂的模型使我们能够对整个放电进行建模。 这些称为全局模型的模型允许确定放电的主要参数(电流、电荷、速度、注入的能量、先导梯度和半径……)[5, 9]。
面向衡量高压材料工程应用角度,用一个针板电极用来计算就足够保证电气安装的安全性。然而,目前所提出的方法远未达到预期,会使得计算结果过于保守。
优化电气工程设计(从而最小化成本)的一种方法是研究不同于经典杆面几何形状的几何形状的介电强度。 在这一贡献中,提出了一种模型,使人们能够动态模拟棒-棒间隙中正放电的连续阶段。 该模型使用 RLC 动态等效电气网络,其参数根据放电特性和几何形状(R、L 和 C 分别为电阻、电感和电容)随时间变化。
2. 正极性棒棒间隙放电发展步骤
在棒-棒间隙的情况下,电极附近的电场足够高,足以在阳极和阴极造成预放电现象。阳极和阴极预放电的相对重要性取决于两个电极上的电场比率,以及在电场分布不对称的情况下它们各自的极性。很明显,如果我们能使电场分布完全对称,其中一个电极接地,施加在另一个电极上的冲击的极性不会影响击穿。
高压实验表明,与电流测量耦合的成帧和条纹模式下的快速相机记录允许我们跟踪正放电的逐步传播以及两个连续步骤之间的复杂现象[5]。
现在让我们来看看在正脉冲电压作用下棒-棒间隙中正放电的不同阶段。在一些文章[1、10、11-13]中已经详细描述了(或至少讨论了)这种放电的结构。从质量上讲,它与受到正脉冲电压[14]作用的点平面间隙中形成的情况非常相似,除了放电的最后一部分:最终跳变。事实上,我们讨论了以下几个阶段:
(1) HV 电极上第一条电晕流注的开始。 (2)根据高压电极的特性和电压波形,存在一段以电极尖端不发光为特征的持续时间不定的时期,即暗期。 (3) 随着电压的增加,电离恢复,放电通道,领导者,向相反的电极发展。 领导者的头部由一个类似于在电极(电晕领导者)上观察到的冠冕组成。 放电的亮度主要是由于领导者的头部,领导者的通道是微弱的。 领导者所走的路径非常曲折,与初始静电场的力线不符。 引导器的引导速度约为 2 cm/μs,其直径约为几毫米。 根据所施加电压的值和形状以及间隙的长度,先导可以停止或到达对面的电极。 (4) 在构成正极引线电晕的拖缆到达负极后,可以注意到从该电极开始的第二个引线的形成以几乎呈指数增长的速度在间隙中向正极前进,并连接正极引线。这种机制称为最终跳跃,如图1所示,其中L+和L-分别是负引线和正引线的轴向长度。
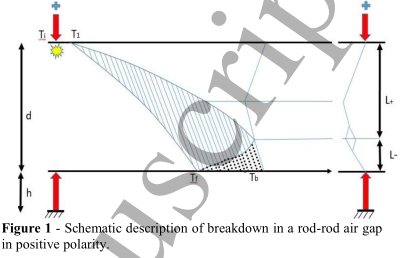
最后请注意,在某些情况下(阴极处的磁场非常高),负引线可能会在最后一次跳跃开始之前形成。
3. 放电的棒-棒间隙模型
3.1 总述
我们提出的模型是基于贝鲁阿尔的团队[15]提出的模型整个放电直到击穿在点平面电极几何。在棒-棒间隙的情况下,电极附近的电场足够高,足以在阳极和阴极上引起预放电现象。阳极预放电和阴极预放电的相对重要性取决于两个电极的电场比例,以及在电场分布不对称的情况下它们各自的极性。很明显,如果我们能使电场完全对称分布,其中一个电极接地,冲击的极性施加到另一个电极不会影响击穿电压。
一般来说,正放电是在其头部有夜光冠的区间内传播的先导放电(图2)。一般的想法是将放电同化为圆柱形导体,并用图3所示的等效电势图来表示它。𝑅𝑖、𝐿𝑖、𝐶𝑖分别是表征放电的电阻、电感和容量,由物理定律、气体理论和电磁场计算确定。使用的传播准则是等效电极头部的电场。正极的头部被等效电极所取代。如果电场足够大(大于Peek的经验关系给出的电场𝐸𝑐),先导通道就会伸长进入电极间隙。否则,它冷却到一个电位保持,除非施加的电压波形将提供重新激活。
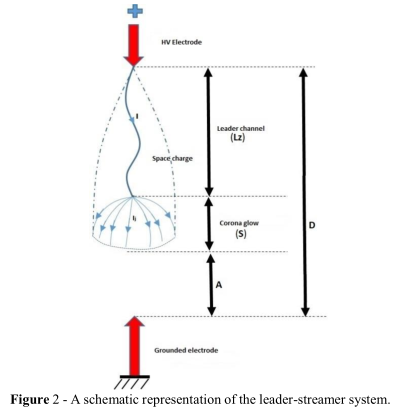
放电的总持续时间被分成几个相等的时间间隔dt (dt是时间步长),从t=0开始。
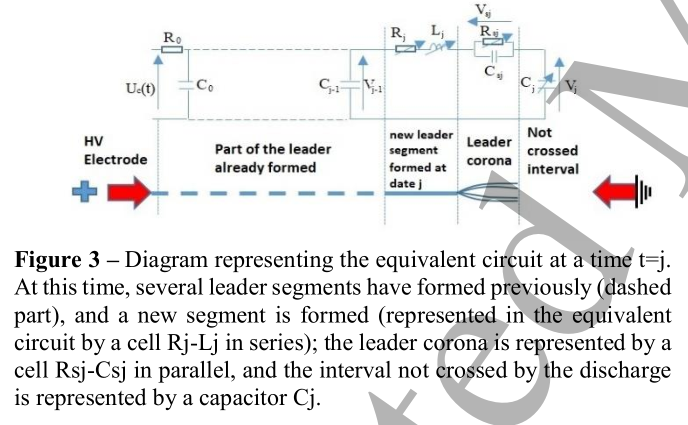
3.2 计算等效电极对导线和电场的影响
在大气隙中,决定放电演化的主要因素(如果不是唯一的)是电场。与杆平面几何的情况不同,在那里可以通过双曲近似[10]推导出电场的解析公式,没有理论公式来计算杆-杆结构的电场,如图2所示。
因此,要估算电场,有必要使用数值计算程序。为此,有几个软件程序可以计算电场(COMSOL, FEMM…)。然而,这些计算是相当繁重和极其耗时的。这就是为什么在这种方法中,我们使用由Kuffel等人给出的静电分析公式来估计球面几何的对称场(图4)。
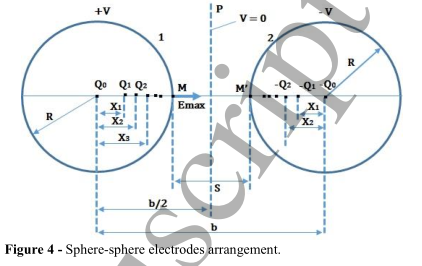
场在M点的解析解是一个无穷级数,通过数值计算,作者得到了解析公式[16]。把这个公式应用到构型上,就会得到
\[E _ { P } = 1.8 \frac { U _ { j } } { ( D - L _ { z } ) } \frac { R _ { e } + 0.5 ( D - L _ { z } ) } { R _ { e } } \tag{1}\]式中𝐸𝑝为等效电极头部的电场;𝑈𝑗是先导头部的电压。
当leader传播时,用[10]给出的半径为𝑅𝑒的等效电极代替它的头部。
\[R _ { e } = \frac { U _ { j } * 0.25 } { U _ { j 0 } ( 1 + \frac { 3.5 } { L } ) } + R _ { e } e ^ { - ( \frac { L _ { z } } { 13.6 R _ { i } } ) } \tag{2}\]式中𝑅𝑖为第一次日冕爆发后的初始等效半径;𝑈𝑗0是施加于活性区域的电压,使等效电极表面的电场等于临界电场𝐸𝑐[10]。
𝐸𝑐取决于电极的形状。对于球形电极,它是如:
\[E _ { c } = [ 1 + \frac { 0.0436 } { \sqrt { R _ { e } \delta } } ] \tag{3}\]其中𝛿为空气因子密度。
2.2 通过等效电路建模先导放电
模型的其余部分包含了[9,17,18]中提出的观点。图5给出了放电建模的流程图。
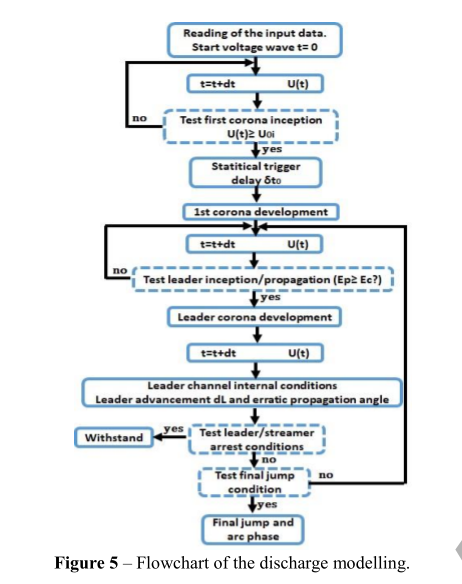
在第一个电晕形成之后,测试先导起始条件(其尖端的电场),直到它满足。然后,第二日冕开始发展。第二电晕形成后,开始了连续流导系统的传播。在每一个时间步,计算导频通道的内部条件(半径、气体密度、压降、电流……)以及未桥接的间隙电容。根据先导长度、沿通道电压降和总电晕电荷的实际值,重新计算其尖端的电场。在此基础上,计算前进拖缆前端的传播特性,以及先导电流I和传播速度v(由能量因素[19]决定)。
实验室研究表明,先导的不稳定传播和与电晕起始相关的统计时滞是导致电压和闪络时间分散的原因[1- 3,5]。通过引入一个以色散参数“a”[10]为特征的概率定律,考虑了不稳定传播。因此,角度φ的概率密度P(φ)为
\[P ( \varphi ) = \frac { | \operatorname { sin } ( \varphi ) | } { 2 a [ 1 - \operatorname { exp } ( \frac { 2 } { a } ) ] } e ^ { [ \frac { \operatorname { cos } ( \varphi ) - 1 } { a } ] } \tag{4}\]3.4 仿真
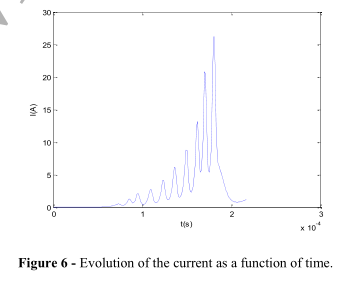
为了测试我们的模型,我们考虑一个6米的杆-杆气隙,在静电对称结构中,受400/10000μs的脉冲。图6 - 8分别描述了先导电流、注入间隙的电荷和先导内部的电位梯度的不稳定演化。我们观察到领导者的平均速度约为2.2 cm/μs (2.2 104 m/s),并且领导者内部的电位梯度随着时间的推移而减小(图8),这突出了领导者的老化,并能够跟踪局部场的演变。
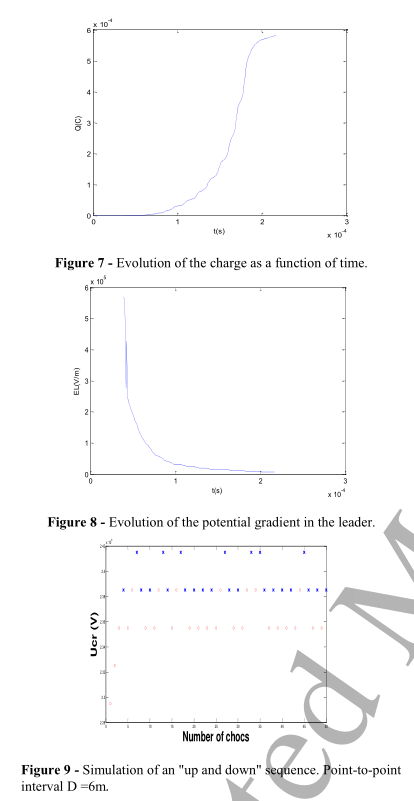
为了估计50%概率击穿电压U50,我们使用“上下”方法,基于U50的最大似然估计和正态分布[20]的标准差σ(图9),得到𝑈50𝑐𝑜𝑚𝑝= 2383 kV, σ= 1.34%
通过使用CRIEPI公式[22]来计算U50
\[U _ { 50 } = k 1080 \operatorname { ln } ( 0.46 D + 1 ) \tag{5}\]我们得到𝑈50𝑐𝑟𝑖𝑒𝑝𝑖= 2288 kV, k=1.6。因此,𝑈50𝑐𝑜𝑚𝑝和𝑈50𝑐𝑟𝑖𝑒𝑝𝑖值之间的相对差异是
\[| \frac { U 50 _ { \text { comp } } - U 50 _ { \text { criepi } } } { U 50 _ { \text { comp } } } | = 0.039 \tag{6}\]这个差额小于4%。因此,可以说这个模型是相当令人满意的。
4. 试验
4.1 简介
2015 年 10 月至 2016 年 6 月期间,我们在 Renardiéres 高压实验室 (EDF) 进行了两次介电测试活动; 主要目的是测量放电期间引线内电流的演变,以及确定 U50 电压和棒平面和棒棒间隔的 k 因子。 考虑的电极间隙 d 在 2 到 5 米之间。 针对雷电脉冲研究每个间隙的行为,并针对批判性冲动。 在实验测量过程中,我们遇到了一些困难,主要困难是:
施加的电应力的持续时间短(双指数电压脉冲,持续时间约为 500 μs,间隔为 10 m)要求放电机制具有非常快的动态和较短的持续时间。 这使得预放电现象的观察变得困难。 在以前的工作中,由于使用了在扫描模式下运行的图像转换器 [21],因此可以观察放电。
预放电的电流强度与回程期间测量的电流强度之间存在巨大差异。 实际上,虽然回程的电流强度可能超过十千安培,但预放电电流为毫安级。 可以在预放电现象和回程发射的光强度之间进行相同的比较。
4.2 试验装置介绍
该实验装置由两个主要部分组成: (1) 一个马克思脉冲发生器和一个相关的高压分压器; (2)一种用于测量包含在高压电极中的电流的系统。

4.3 电流配置
无论考虑的间隔如何,电流分布通常具有相同的形状。 因此,我们将以下内容限制在对棒平面配置中 2 m 间隔的电流分布的研究,然后是棒棒配置。