Modelling of the leader current with an equivalent electrical network

长间隙先导电流等效电气网络模型

摘要

本文的目的是提出一种先导电流的电学模型，该模型与描述振荡冲击电压产生的电流有关。该模型允许评估沿先导通道的先导电流、电荷和电位分布。引线的物理参数用等效网络来描述。通过将这些参数积分到测试电路中，我们能够推导出气隙中任一点的电流和电荷，然后将我们的结果与实验产生的大气隙放电的实验结果进行了比较。该模型给出的电流和电荷特性与实验结果吻合较好。

1. 引言

气体排放中发生的基本过程过去是，现在仍然是许多研究的主题(Les Renardikres group 1972,1974,1977，Meek and Graggs 1978，Gary er A1 1984，Gallimberti 1979)。气体放电的物理机制非常复杂。它们取决于许多物理和几何参数，例如电极间隙。在这项工作中，较长的气隙是首要考虑的问题。在这样的空隙中发生的现象可以概括为以下几个方面。

放电在产生适当位置的自由电子的时间滞后之后开始。第一个电晕代表了第一个可观察到的电离过程，通常采取丝状通道或流光的形式。在某些情况下，第一次日冕之后是一个或多个暗期。

第二个可观察到的现象发生在第一次日冕之后。这是一个直径几毫米的电离通道，很热，是一个相对好的导体：引线。在它的顶端，产生了一个新的日冕，显示出一些丝状结构的证据，这种结构使先导通道前面的空气电离。正是通过这种机制，维持了显影放电中的电流流动，改变了间隙中的电场分布。随着外加电压的增加，引线沟道沿平面方向增长。

先导传播的最后阶段被称为“最后一跳”。这是引线传播的终端状态，其特征是电流迅速增加(回程)，这不可避免地会导致间隙短路。

许多工作致力于分析表征放电的不同参数，如电流、电荷、传播模式、速度和辐射电磁场。

了解放电电流是非常重要的，特别是在评估遭受直接撞击(例如触电、起火和损坏电气设备)的系统中可能发生的损坏时。此外，电流还会辐射电磁场。众所周知，这些辐射场与工程系统(通信设备、集成到不同系统中的电子设备、导航计算机等)相互作用。

对长气隙放电的动力学方面，特别是对先导电流的模拟，将对评估损害并最终防止这种损害有很大帮助。这是许多作品的主题(Gary er A1 1984，Gallimberti 1979，Ortega 1992，Klewe a/1974)。

最有用的描述领导者发展的模型要么基于局部热力学平衡的存在，要么基于非平衡情况的存在。第一个假设是许多争论的主题(Les Renardkes group 1977，Gary er，a/1984，Klewe et a/1974)。我们下面开展的工作涉及到第二种情况。

在这篇文章中，我们提出了一个领先者的等效电路模型，使得人们可以得到它的时空演化。这样的模型使用了物理定律和气体放电理论。此外，它比纯粹的经验模型更简单，后者使用特殊的特定条件，或者使用物理条件，后者通常非常复杂。将该等效电路模型应用于点-面间隙。假设引线是一根长圆柱形的导体。它将由单根导线的RC单元(R和C分别为电阻和电容)表示。我们在模型中使用的R值和C值是从其他研究人员对正引线(电压、电流、电荷、条纹照片)的实验结果得出的典型值。对于给定的电压形状，特别是振荡脉冲电压，我们进一步用我们的模型确定了电流和电荷。然后将结果与实验结果进行比较(Ortega ETA[1991，Ortega 1992)

2. 先导的时空发展

作为起点，我们假设引线可以用一个如图1所示的等效网络来表示。$R_0$是平面电极电阻，其典型值在100-200Ω范围内(Johannet 1987，Ratnamahilan and Hook 1993)。在这项工作中，$R_0$的值被设置为100Ω。$C_0$可以使用球面近似(假设两个电极分别是半径为$R_p$和$R_P+D$的同心球体；D为间隙长度，$R_p=2 mm$为电极半径)，并考虑其值等于球面容量的一半：

\[C _ { 0 } = 2 \pi \varepsilon _ { 0 } \frac { ( D + R _ { \rho } ) R _ { p } } { D } \tag{1}\]

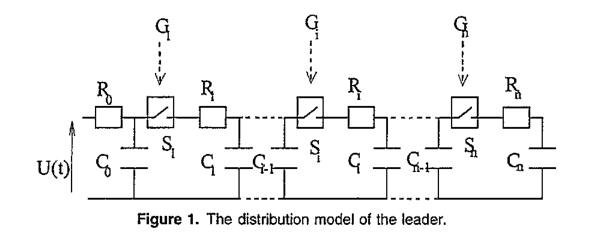
当引线传播时，这对应于开关$S_i$(与脉冲发生器$G_i$相关联的接触器)闭合，并且启动的电势波将如图2所示。因此，流经线路的电流由下式给出

\[I _ { i } ( t ) = C _ { i } ( x ) \frac { d V _ { i } ( t ) } { d t } \tag{2}\] \[I _ { i } ( t ) = \frac { V _ { i } ( t ) - V _ { i - 1 } ( t ) } { R _ { i } ( x ) } \tag{3}\]

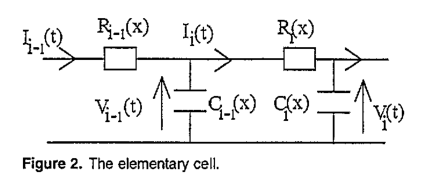
X是先导通道的轴向长度。

\[C _ { i - 1 } ( x ) \frac { d V _ { i - 1 } ( t ) } { d t } = I _ { i - 1 } ( t ) - I _ { i } ( t ) \tag{4}\]

通过将方程(2)和(3)代入方程(4) ，得到电压，然后得到先导电流

\[I ( t ) = \frac { U ( t ) - V _ { 0 } ( t ) } { R _ { 0 } } \tag{5}\]

$V_0(t)$是$C_0$电容电压。

注入间隙的空间电荷可通过将电流积分计算为

\[q ( t ) = \int _ { 0 } ^ { t } I ( t ) d t \tag{6}\]

图3为一般图表，显示积分器装置与图1所示先导器的等效电路的连接

\[V ( t ) = \frac { k R _ { 0 } } { C } \int _ { 0 } ^ { t } I ( t ) d t \tag{7}\]

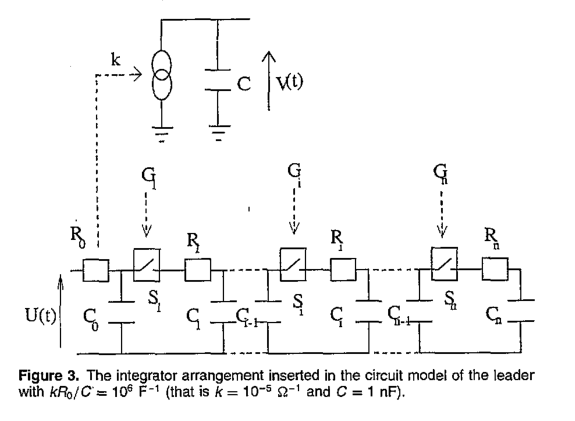
k是跨导。

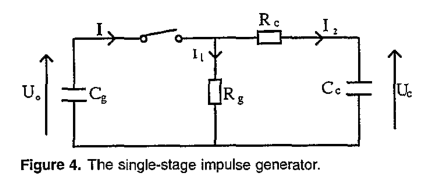
已经知道，电流和先导的电荷取决于施加在电极间隙的电压。在下面，我们考虑一个类似 ortega et a1(1991)和 ortega (1992)所使用的脉冲电压，以便将我们的结果与这些作者所获得的结果进行比较。这种形式的电压由阻尼振荡在双指数脉冲上的叠加构成。用3mv，48.6 kj Marx发生器产生双指数脉冲，即在不同峰值电压下的正切换脉冲。双指数电压的表达式可以通过单级脉冲发生器电路获得。这包括一个电容器 C，它被充电到所需的电压，并通过一个电路放电，其常数可以调整，以便给出所需形状的冲击电压。单级发电机的基本电路如图4所示。元素 $R_c$ 和 $C_c$，控制前面的$R_g$ 和 $C_g$，冲击电压的尾部。对电路的分析，如图4所示，允许我们得到输出电压 $u_c(t)$的表达式。通过使用拉普拉斯变换属性，我们已经

\[\frac { U _ { 0 } } { p } = I _ { 1 } R _ { g } + ( I _ { 1 } + I _ { 2 } ) \frac { 1 } { p C _ { g } } \tag{8}\]

按照理解，公式（8）的右面应该是指的开关断口两端的电压，此处的$p = jw$，整个公式（8）没看明白

\[I _ { 1 } R _ { g } = I _ { 2 } ( R _ { c } + \frac { 1 } { p C _ { c } } ) \tag{9}\] \[U _ { c } ( p ) = I _ { 2 } / ( p C _ { c } ) \tag{10}\]

将方程(8)和(9)代入(10) ，重排后得到

\[U _ { c } ( p ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { 1 } { p ^ { 2 } + b p + c } \tag{11}\]

或者

\[U _ { c } ( p ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { 1 } { ( p + \frac { 1 } { T _ { a } } ) ( p + \frac { 1 } { T _ { b } } ) } \tag{12}\] \[b = \frac { 1 } { R _ { c } C _ { c } } + \frac { 1 } { R _ { g } C _ { g } } + \frac { 1 } { R _ { c } C _ { g } } \tag{13}\] \[c = \frac { 1 } { R _ { c } R _ { g } C _ { c } C _ { g } } \tag{14}\] \[T _ { a , b } = \frac { 2 } { b \pm ( b ^ { 2 } - 4 c ) ^ { 1 / 2 } } \tag{15}\]

其中$ 1/T_a $和$ 1/T_b $是方程$ p^2 + bp + c = 0$的根。

最后，通过反演方程(12)中的拉普拉斯变换，我们得到

\[U _ { c } ( t ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } [ \operatorname { exp } ( - \frac { t } { T _ { a } } ) - \operatorname { exp } ( - \frac { t } { T _ { b } } ) ] \tag{16}\]

因此我们看到电压 i (t)的形状取决于时间常数$ 1/T_a $和$ 1/T_b $，这些表达式在文献中已知(ilkowski 和 kosztaluk 1985)

\[T _ { a } = ( T _ { 2 } - T _ { cr } ) / 0.7 \tag{17}\] \[T _ { b } = \frac { T _ { a } } { \operatorname { exp } [ 1.35 + 1.2 \operatorname { ln } ( T _ { 2 } / T _ { cr } ) ] } \tag{18}\]

最大值$U_c(t)$将为

\[t = T _ { cr } = \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } \operatorname { ln } ( \frac { T _ { a } } { T _ { b } } ) \tag{19}\]

其中$ 1/T_a $，$ 1/T_b $，$ 1/T_2 $和$ 1/T_cr $分别是上升时间，下降时间，半值时间，峰值时间和振幅因子。

设

\[\frac { T _ { a } T _ { b } } { ( T _ { a } - T _ { b } ) R _ { c } C _ { c } } = 1 \tag{20}\]

我们可以将$ U_c (t) $写作

\[U _ { c } ( t ) = U _ { 0 } [ \operatorname { exp } ( - \frac { t } { T _ { a } } ) - \operatorname { exp } ( - \frac { t } { T _ { b } } ) ] \tag{21}\]

其中

\[C _ { c } = \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } \frac { 1 } { R _ { c } } \tag{22}\]

选择脉冲发生器的组成元素，使得$R_g$和$C_g$分别比$R_c$和$C_c$大。

通过方程式(15)的检验，我们得到了

\[T _ { a } \approx R _ { c } ( C _ { g } + C _ { c } ) \tag{23}\] \[T _ { b } \approx R _ { g } \frac { C _ { g } C _ { c } } { C _ { g } + C _ { c } } \tag{24}\]

这些方程可以让我们推导出$R_g$和$C_g$。另一方面，取$\delta = T_a / T_b$，我们可以推导出$U_0$(aguet and ianoz 1987)

\[U _ { 0 } = \frac { U _ { cr } } { ( \delta ^ { 1 / ( 1 - \delta ) } - \delta ^ { \delta / ( 1 - \delta ) } ) } \tag{25}\]

最后，$U_c (t)$将如图5的框图所示给出。

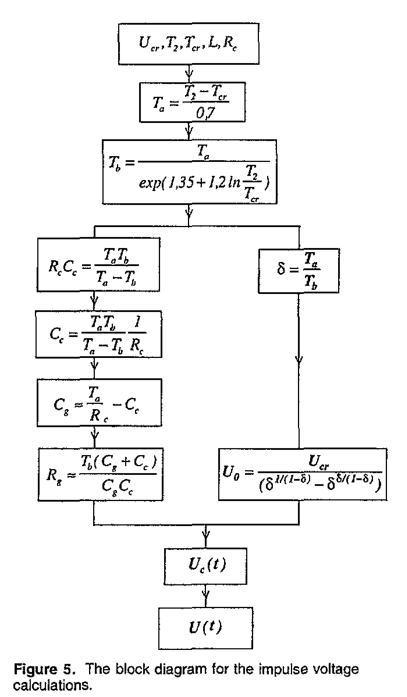
为了在双指数脉冲上叠加电压振荡，在电容分压器和高压电极(ortega et al 1991，ortega 1992)之间安装了电感 l (7m h < l < 110mh)。

这个电压的形状可以通过使用图6所示的冲击等效电路的元件的模拟得到，其中L将振荡的频率增加1/T。

从上面可以看出，领导者的时空参数(电流和电荷)的知识需要$ C_i $和$ R_i$元素的知识(图1)。