EMTP Theory
此部分会逐步更新,是自己学习的一个过程。
1. EMTP求解方法
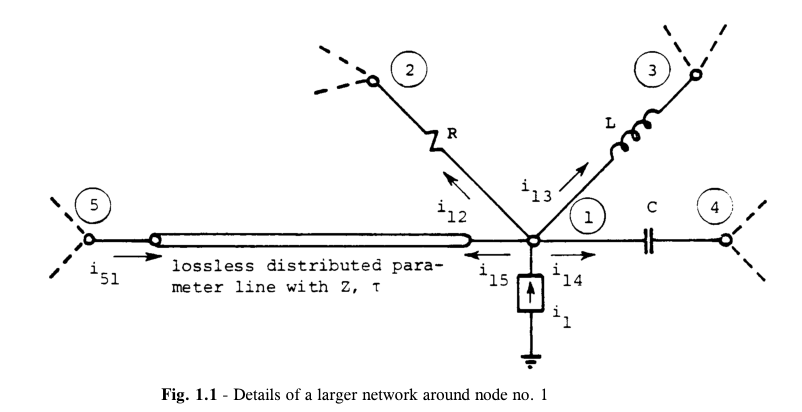
这是一个标准的电力网络,里面有电阻R、电感L、电容C、输电线路以及电流源激励。
\[i_{12}(t)+i_{13}(t)+i_{14}(t)+i_{15}(t)=i_{1}(t)\] \[i_{12}(t)=\frac{1}{R}\left\{v_{1}(t)-v_{2}(t)\right\}\] \[v=L \frac{d i}{d t}\] \[\frac{v(t)+v(t-\Delta t)}{2}=L \frac{i(t)-i(t-\Delta t)}{\Delta t}\] \[i_{13}(t)=\frac{\Delta t}{2 L}\left\{v_{1}(t)-v_{3}(t)\right\}+h i s t_{13}(t-\Delta t)\] \[h i s t_{13}(t-\Delta t)=i_{13}(t-\Delta t)+\frac{\Delta t}{2 L}\left\{v_{1}(t-\Delta t)-v_{3}(t-\Delta t)\right\}\] \[i_{14}(t)=\frac{2 C}{\Delta t}\left\{v_{1}(t)-v_{4}(t)\right\}+h i s t_{14}(t-\Delta t)\] \[h i s t_{14}(t-\Delta t)=-i_{14}(t-\Delta t)-\frac{2 C}{\Delta t}\left\langle v_{1}(t-\Delta t)-v_{4}(t-\Delta t)\right\}\]以上是电阻、电感、电容的计算方程,相对简单。
对于传输线,也就是node1~node5,先不考虑线路的阻抗损耗,则传输线方程为: \(-\frac{\partial v}{\partial x}=L^{\prime} \frac{\partial i}{\partial t}\)
\[-\frac{\partial i}{\partial x}=C^{\prime} \frac{\partial v}{\partial t}\]其中
$\mathbf{L}^{\prime}, \mathbf{C}^{\prime}$=单位长度传输线的电感和电容
x=从起始端的距离
传输线备注:
一个集中参数的传输线,若设单位距离很短,则可以近似用下图进行表示。

根据基尔霍夫定律有 \(u(z, t)-R \Delta z i(z, t)-L \Delta z \frac{\partial i(z, t)}{\partial t}-u(z+\Delta z, t)=0\)
\[i(z, t)-G \Delta z u(z+\Delta z, t)-C \Delta z \frac{\partial u(z+\Delta z, t)}{\partial t}-i(z+\Delta z, t)=0\]改写成微分方程形式 \(\frac{\partial u(z, t)}{\partial z}=-R i(z, t)-L \frac{\partial i(z, t)}{\partial t}\)
\[\frac{\partial i(z, t)}{\partial z}=-G u(z, t)-C \frac{\partial u(z, t)}{\partial t}\]若忽略线路电阻和对地电导,则有 \(\frac{\partial u(z, t)}{\partial z}=-L \frac{\partial i(z, t)}{\partial t}\)
\[\frac{\partial i(z, t)}{\partial z}=-C \frac{\partial u(z, t)}{\partial t}\]