《Modeling Study for High Impedance Fault Detection in MV Distribution System》
Cui T, Dong X, Bo Z, et al. Modeling study for high impedance fault detection in MV distribution system[C]//2008 43rd International Universities Power Engineering Conference. IEEE, 2008: 1-5.
DOI: 10.1109/UPEC.2008.4651507
摘要
建模研究为高阻抗故障(HIF)检测的研究提供了一种更有效,更灵活的方法。 能够揭示HIF的大多数功能的准确模型非常重要。 在对记录的测试结果进行广泛研究的基础上,本文总结了一组最常见且令人满意的特征:电弧特征,非线性,随时间变化的电阻和随机性。 已经公开了可以重构这些特征的仿真建模方法。 利用ATP-EMTP模型,提出了一种基于一系列时变接地电阻和动态电弧电阻的HIF模型。 为了重建HIF的这些细节特征,已经测试了电弧参数及其影响。 随机因素已被引入该模型的HIF行为不稳定。最后,通过将该模型应用于模拟的MV系统,初步讨论了几种特征提取和检测方法。
1. Introduction
高阻抗故障(HIF)通常定义为导体在非导电表面上的不必要的电接触,从而限制了故障电流,使常规继电器的检测水平降低[1]。 由于HIF通常是由在公众范围内被压倒但通电的导体引起的,并且大多带有电弧,因此对人身安全和财产安全构成了巨大威胁。 因此,HIF检测早已成为保护工程师关注的重点。但这仍然是一个未解决的问题。
由于没有明显的稳态故障特征,因此基本的短路模型不适合HIF研究。因此,使用特殊的波形和故障电流/电压的不稳定行为来识别此类故障。 罗素与TAMU的研究人员进行了各种现场测试。 已经使用了谐波能量,频谱,电弧模式和随机性等HIF特征,并提出了一种具有专家系统的复合算法[2]。 在各种细节特征中,三次谐波匝数更加实用和独特,三次谐波的相位角和幅度被证明是HIF的独特特征[3] [4],而大多数情况下,随机故障间歇是HIF的共同特征。 在大多数阶段测试中[2] [5]。
以前有关HIF检测的许多研究高度依赖于现场测试。 昂贵的阶段测试和不可预测的实验条件禁止在各种系统条件下对HIF进行全面研究。 因此,基于实际测试的结果,对于HIF检测的研究非常必要的是可以准确表示这些特征的数学模型。 已经提出了几种HIF模型:Nam通过使用时变电阻来拟合HIF来模拟HIF [6],Michalik使用弧形模型来描述HIF的详细波形[7],而Elkalashy也使用通用模型 表示HIF电弧故障特征的电弧模型[8]。
由于某些最显着的波形失真是由电弧引起的,例如周期性的失超,重燃,随机故障爆发,以及更大范围内的故障非线性。 弧模型的研究是HIF建模的方法。尽管HIF电弧与大多数电弧模型不同,后者专注于高压开关设计,超高压线路故障定位或自动重合闸系统[9]。 对于HIF,电弧通常位于不受限制的空间内,具有较短的长度和较低的系统电压。 因此,应指定弧的参数。
本文在对现场数据进行研究的基础上,对HIF的机理进行了分析和总结。 详细介绍了具有电弧热方程式和可变接地电阻的仿真模型。 弧模型参数是所提出模型的一个非常重要的方面。通过全面扫描弧的参数,可以重构HIF弧的不同行为并进行相应分类。 包括随机性和瞬态性在内的其他因素也旨在表示配电系统中HIF功能的更多功能。 利用随机因素,已经重建了间歇行为。 在使用分布式参数馈送器测试模型时,已揭示出HIF的快速瞬态功能。
本文的组织结构为:第二部分是现场测试数据和HIF机制的摘要; 使用ATP-EMTP进行建模的方法和模型的检验在第三部分中; 在第四节中,使用该HIF模型对MV系统进行了仿真,还初步揭示了一些功能。
2. HIF现场数据和机制
A. 现场数据
以下是从德州电力公司,台湾电力公司和TAMU的实际现场测试中借来的数字,它们代表了各种HIF阶段测试波形。 图1(a)和(b)说明了这些详细的波形失真。 图1(c)说明了较长时间范围内HIF的随机性。
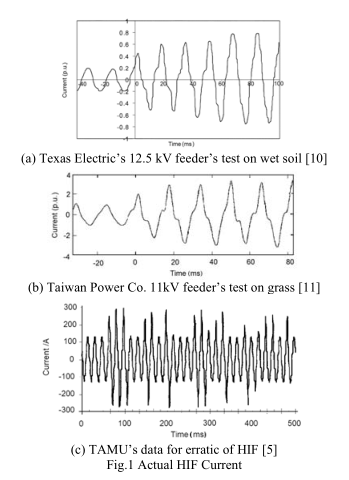
上面的典型高阻抗故障电流图表明了HIF特性的不同方面:1)在详细范围内,过零电流附近的特定畸变是电弧[7] [8]的明显特征; 2)在每个周期的范围内,由于接地电阻非线性[3] [4],波形看起来像正常的正弦波电流,由于谐波而失真。 3)在更长的时间范围内,HIF会以间歇性模式爆发并熄灭[2] [5]。
在各种文档中,这些功能被引用为HIF的最常见特征,因此已经开发出许多检测技术来利用这些功能。
B. HIF机制-电弧
尽管电流波形在以上不同情况下的行为有所不同,但仍有一些HIF的潜在机制有助于上述这些共同特征。 本文工作的目的是基于这些机制对HIF进行建模。 弧及其相应的影响在这些方面起着重要作用。
1)典型的电弧特征:与正常的短路故障不同,HIF产生的稳态电流有限,对于典型的12.5 kV系统,故障电流范围为10至50A [1]。 因此,弧的细节特征不再可忽略。 电弧实际上塑造了特殊的细节,例如穿越零淬火和故障电流的重新点火。
2)引起谐波失真的接地电阻的非线性也可以通过故障/电弧路径的热特性来简单地解释:当电流下降时,注入功率也下降,由于冷却而造成功率损耗, 故障路径将减小,从而使电流的绝对值低于相交零点附近的标准正弦波,因此,将谐波注入故障电流。
3)在大多数HIF情况下,电弧放电路径是在空气中且冷却条件较好的情况下进行的,这使电弧更容易熄灭,并导致HIF电流断断续续。其他事实(例如导体的随机摆动和电弧运动)也有助于HIF的间歇/随机功能。
如图1所示,并非每个HIF都具有所有这些特征,但是所有这些特征都导致了HIF的一个相对共同的组成部分:断层电弧,随机的熄灭/重击行为以及更大的接地电阻率。 而本文的HIF模型就是基于这些机制的。
3. HIF 建模
A. 用ATP-EMTP建立模型
在本节中,对10 kV系统中的典型HIF进行了分析和建模,通过选择具有适当参数设置的电弧模型以及在电弧模型中包括随机因素,可以实现上述空气电弧特性。
大多数HIF是单相接地故障[1]。 在故障点,HIF由两部分组成:1)导体与非导体之间的动态交流电弧; 2)故障路径电阻,通常是树木,建筑物或地面。因此,HIF模型可以由一系列两个可变电阻器来表示:瞬态电弧电阻器和稳态较高故障路径电阻器[6]。 前一个$R_{ARC}$描述了由电弧引起的每个周期的波形的细节(熄弧和重燃)。 后一个$R_P$表示根据接地电阻率和介电条件而变化的故障路径电阻。
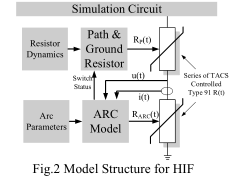
由ATP-EMTP的不同MODELS模块控制的两个随时间变化的电阻已用于构建这两个电阻。
对于动态电弧电阻$R_{ARC}$,有多种建模方法。 黑匣子模型仅通过使用外部信息(例如电弧电流和电压)来描述电弧的电气特性,因此它们更适合于本研究。 Cassie模型和Mayr模型是最有代表性的电弧模型,它们基于具有相似思想的热方程:电弧电导与电弧放电路径中的热量有关,但是它们具有不同的恒定参数假设。 这两个模型及其推导已广泛用于电弧的研究,例如断路器,自动重合闸系统和故障定位的研究[9]。 对于我们对HIF弧的特定研究,选择了Mayr方程,因为它最适用于小电流,尤其适用于表示电弧过零点的特性。
Mayr方程是。
\[\frac{1}{g} \frac{d g}{d t}=\frac{d \ln g}{d t}=\frac{1}{\tau_{m}}\left(\frac{E i}{P_{m}}-1\right)\tag{1}\]式中,$g$是单位长度的电弧电导。 $τ_m$是时间常数,表示电弧的温度惯性。 $P_m$是每长度电弧的功率损耗; $E$是每长度的弧径电势; $i$是电弧电流。 在这个方程中,电弧的热状态由两部分表示:热源是电能注入$E_i$; 热损失是假设的恒定功率损失$P_m$; 热条件对电导$g$的变化的影响具有一个以$τ_m$表示的时间延迟。
对于交流电弧,当电流在每个周期接近零,$Ei <P_m$时,电弧内部的热量将减少,电导$g$也将减少,由于时间常数$τ_m$,$g$的变化将滞后。 因此,从当前的零交叉点开始会有最低电导点的延迟,从而使电弧持续存在,并在每个周期内都围绕零交叉点出现灭弧和重燃。
另外,谐波,特别是具有特定相位的三次谐波也可以简单地进行解释:如果三次谐波都过零时与基波相比的相位大约为180º,则三次谐波会减弱基波电流,使其低于理想正弦波 在零点附近波动。 这也是公式(1)的意义。
对于上述典型的Mayr电弧模型,具有更长的时间延迟$τ_m$和更低的功率损耗$P_m$(较差的冷却条件),电弧将更可能稳定持续。 矛盾的是,更好的冷却条件意味着,由于较低的$τ_m$和较高的$P_m$,排出路径内部的热量将更快地散发。 因此,在更好的冷却条件下,电弧可能更容易完全自熄。 通常,Mayr的模型用于有限空间(开关室)中的断路器设计。 对于露天故障电弧,冷却条件($τ_m$和$P_m$)和电弧形状(由电弧长度表示)是可变的,应加以调整。 而且,露天的更好的冷却条件将使电弧更容易熄灭。 这导致了随机性特征。
对于状态稳定电阻$R_P$,本文估算的主要考虑因素是接地电阻率,该值随土壤类型,温度,湿度和许多其他因素而变化。 典型的接地电阻率ρ从中等水平的300Ωm(在页岩中)到非常高的水平(在粗砂中)[3000]变化[12]。 假设故障点处的HIF由半径为$r_1 = 5 cm$的圆柱电极表示。接地电阻可以通过$R =ρ/(2πr_1)$来计算。 电阻值的范围为1kΩ至10kΩ。因此,在此模型中,$R_P$的变化范围为10kΩ至5kΩ,并沿时间轴变化。
对于使用EMTP的MODELS进行建模,从电源电路中获取电弧的电压和电流,并在每个模拟步骤中将其馈入MODELS的输入,然后根据这些输入,通过以下方式,MODELS可以用于求解(1):
\[\begin{aligned} (\ln g)_{t} &=(\ln g)_{t_{0}}+\int_{t_{0}}^{t} \frac{1}{\tau_{m}}\left(\frac{E i}{P_{m}}-1\right) d t \\ &=(\ln g)_{t-\Delta t}+\frac{\Delta t}{2}\left(\frac{1}{\tau_{m}}\left(\frac{E i}{P_{m}}-1\right)_{t-\Delta t}+\frac{1}{\tau_{m}}\left(\frac{E i}{P_{m}}-1\right)_{t}\right) \end{aligned}\tag{2}\]$t_0$是故障开始时间,$t$是当前仿真时间。 $Δt$是时间步长。 订阅t表示当前时间步的数据,t –Δ t表示最后计算步的历史数据。 然后,结果g将在下一个模拟步骤中作为可变电弧电阻应用于电源电路。
B. HIF模型结果的示例
下图是一个HIF模型的电弧电流示例的结果,考虑到室外的冷却条件,电弧功率损耗$P_m$设置为8 kW / m(正常值为3 kW / m),电弧 长度为5厘米,时间常数$τ_m$设置为600us。
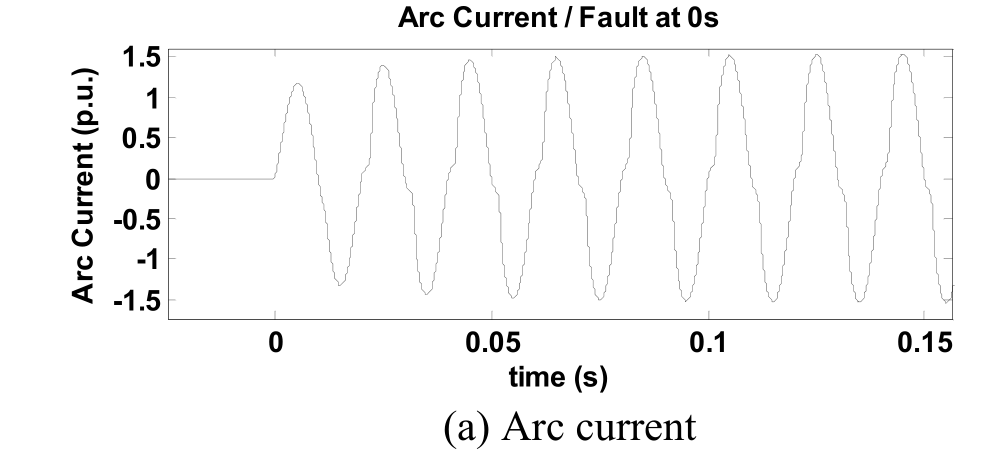
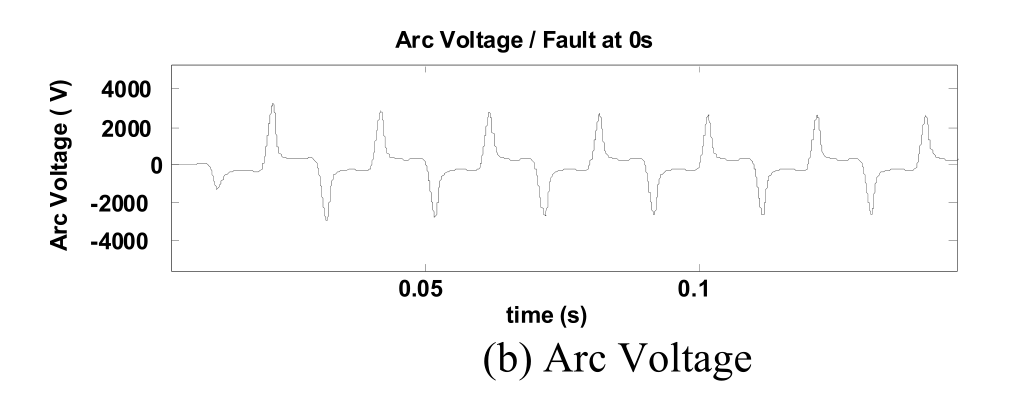
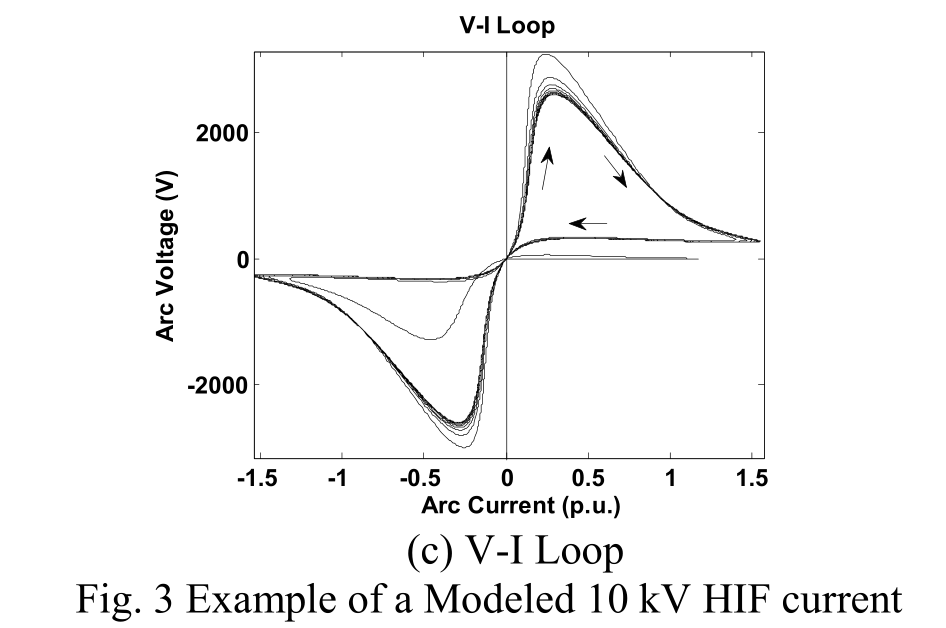
图3中的电压和电流的测量是在弧点处进行的。 但是,对于位于母线的故障检测器,由于较低的电弧电压和较高的路径阻抗,因此难以获得准确的电弧电压。 对于平衡接地系统,该电弧电流可以在相线接地故障的情况下从中性线电流获得。
C. 测试和辨识电弧参数
对于此动态电弧模型,三个参数:$P_m$,$τ_m$和电弧长度确定它是自熄电弧还是稳定持续电弧,并且这些参数还会导致HIF电流的形状不同以及电弧畸变程度。
具有更好的冷却条件:更大的功率损耗或更低的延时,HIF电弧往往更容易熄灭。
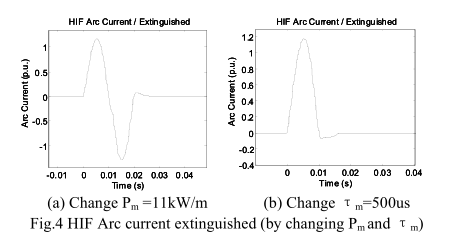
在图4中,当电流过零时,HIF电弧电流消失,这种机制有助于实现HIF电弧最常见的间歇性特征。
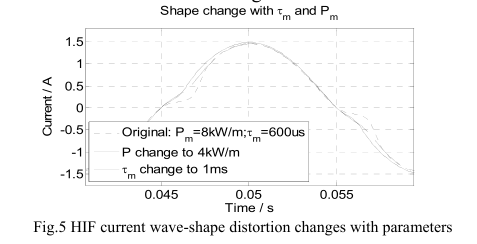
通过不同的参数,此HIF电弧电流的形状会发生变化,如图5所示。
对于持续稳定的电弧,周期性失真将随着功率损耗的增加和/或时间常数的减小而增加。 换句话说,在更好的冷却条件下变形会更高。
此外,如前所述,如果冷却条件达到更高的水平,电弧可能会自行熄灭。 通过在10 kV交流电压源下扫描该模型的所有三个参数,下图显示了熄灭和持续电弧放电情况的边界。

在图6中,右下方是“电弧稳定持续”参数区域:较低的功率损耗和较高的时间常数表示较差的冷却条件。 相反,左上方的“电弧自熄”参数区具有更好的冷却条件,电弧将在爆裂后几个周期在零交叉点处自熄。 如图1(c)所示,随机重发会导致间歇性中断。 此外,如图5所示,参数在边界附近的持续弧似乎具有较高的周期性失真。
D. 修正(随机因素)
由于复杂的现场情况,这三个电弧参数是可变的。 因此,通过将随机因素引入这些参数,开发了一种HIF模型,旨在重建第二节中的随机特征。
在图6中,当将正常参数设置在持久区域的边界附近,并在这些参数之一中引入随机偏差时,可以描述随机间歇但仍具有详细弧特征的波形:
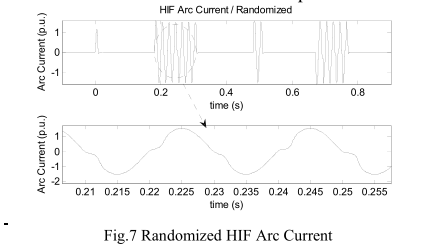
在图7中,时间常数设置为$τ_m = 600us·(1±0.25·Rnd)$,其中Rnd是由EMTP生成的均匀分布的随机数,范围为0到1。$P_m = 9 kW / m$, 弧长为5 cm,位于图6中的边界之一。 电流过零后的每半个周期,将产生一个新的$τ_m$,为下一次电流过零做准备。
通过这种方式,HIF弧模型具有详细特征以及间断/随机特征。 在下一部分中,此模型用于模拟MV系统中,以进一步提取特征。
4. 系统仿真及检测方法
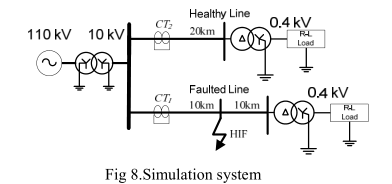
A. 系统仿真
本节采用中性点接地系统。 使用HIF模型模拟相接地HIF。
主要采样的模拟信号是零线电流,在平衡的接地系统中,该零线电流被认为等于相线对地电流。
HIF在具有线性R-L型负载的20公里架空线中间进行。 分布式参数用于表示HIF的瞬态特征。
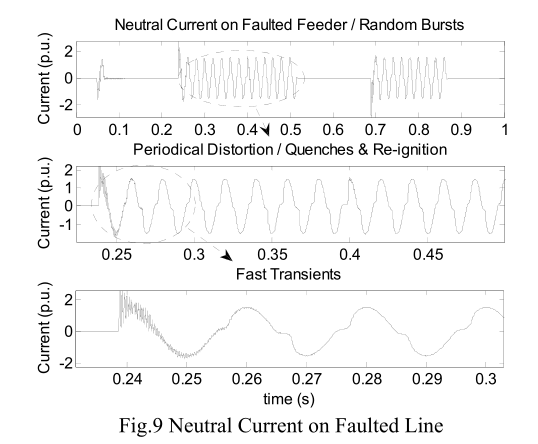
故障电流的结果在图9中。 这些重要和最常见的特征已由该模型揭示:1)随机爆发并熄灭; 2)电弧熄灭和点燃; 3)周期性失真或谐波; 4)此外,在实际的分布式参数系统中,以较高的采样速度,可以捕获由故障传导的初始引起的快速瞬变,并且可以用作另一个独特的特征。
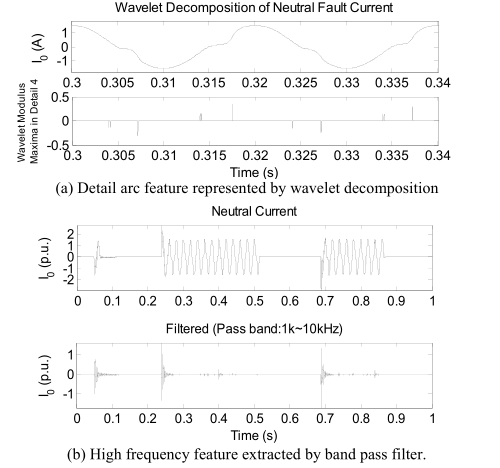
B. 特征提取
小波分解已被用于通过电弧熄灭和重燃来提取细节失真,类似的小波和处理方法已在[13]中进行了详细介绍。
频率限制为1 kHz至10 kHz的带通滤波器用于提取HIF的快速瞬态特征。
根据[3] [4],谐波特征主要由三次谐波与基波的相位差以及与基波的比表示。
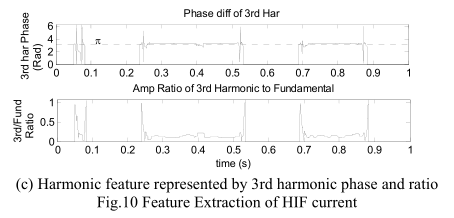
5. 结论
与昂贵的现场测试相比,通过建模进行的HIF检测研究是一种更有效,更灵活的方法。 本文通过对高阻抗电弧故障机理的研究,利用ATP-EMTP模型对细节波形以及间歇性特征进行了解释和重构。通过将此模型应用于分发系统,一些最独特的功能已经被揭示出来。 最后,提出了几种初步的方法作为特征提取的一个例子。
参考文献
[1] PSRC Working Group D15, “High Impedance Fault Detection Technology,” Report of PSRC. March 1, 1996. [Online]. Available: http://grouper.ieee.org/groups/td/dist/documents/highz.pdf .
[2] R. Patterson, W. Tyska, B. D. Russell, and B. M. Aucoin, “A Microprocessor-Based Digital Feeder Monitor with High-Impedance Fault Detection,” in 47th Annual Conference for Protective Relay Engineers Texas A&M University, College Station, Texas, USA, 1994.
[3] A. E. Emanuel, D. Cyganski, J. A. Orr, S. Shiller, and E. M. Gulachenski, “High impedance fault arcing on sandy soil in 15 kV distribution feeders: contributions to the evaluation of the low frequency spectrum,” Power Delivery, IEEE Transactions on, vol. 5, pp. 676-686, 1990.
[4] D. I. Jeerings and J. R. Linders, “Unique aspects of distribution system harmonics due to high impedance ground faults,” Power Delivery, IEEE Transactions on, vol. 5, pp. 1086-1094, 1990.
[5] C. L. Benner and B. D. Russell, “Practical high-impedance fault detection on distribution feeders,” Industry Applications, IEEE Transactions on, vol. 33, pp. 635-640, 1997.
[6] S. R. Nam, J. K. Park, Y. C. Kang, and T. H. Kim, “A modeling method of a high impedance fault in a distribution system using two series time-varying resistances in EMTP,” in Power Engineering Society Summer Meeting, 2001. IEEE, 2001, pp. 1175-1180 vol.2.
[7] M. Michalik, W. Rebizant, M. Lukowicz, Seung-Jae Lee, and SangHee Kang, “High-impedance fault detection in distribution networks with use of wavelet-based algorithm,” Power Delivery, IEEE Transactions on, vol. 21, pp. 1793-1802, 2006.
[8] N. I. Elkalashy, M. Lehtonen, H. A. Darwish, M. A. Izzularab, and A. M. I. Taalab, “Modeling and experimental verification of high impedance arcing fault in medium voltage networks,” Dielectrics and Electrical Insulation, IEEE Transactions on [see also Electrical Insulation, IEEE Transactions on], vol. 14, pp. 375-383, 2007.
[9] Y. Li, X. Dong, Z. Q. Bo, N. F. Chin, and Y. Ge, “Adaptive reclosure using high frequency fault transients,” in Developments in Power System Protection, 2001, Seventh International Conference on (IEE), 2001, pp. 375-378.
[10] A. A. Girgis, W. Chang, and E. B. Makram, “Analysis of highimpedance fault generated signals using a Kalman filtering approach,” Power Delivery, IEEE Transactions on, vol. 5, pp. 1714-1724, 1990.
[11] H. Shyh-Jier and H. Cheng-Tao, “High-impedance fault detection utilizing a Morlet wavelet transform approach,” Power Delivery, IEEE Transactions on, vol. 14, pp. 1401-1410, 1999.
[12] “IEEE guide for measuring earth resistivity, ground impedance, and earth surface potentials of a ground system” IEEE Std 81-1983, 1983.
[13] Xinzhou Dong, Yaozhong Ge, Jiali He, “ Surge impedance relay,” Power Delivery, IEEE Transactions on, vol. 20, pp. 1247-1256, Apr. 2005.