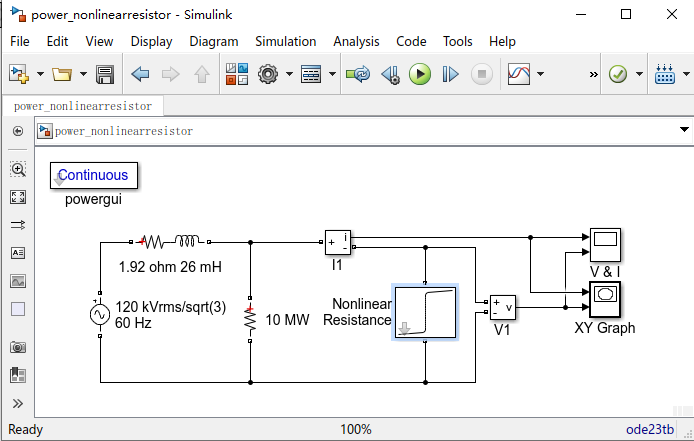
1. 建立武汉考核场基础PSCAD模型
1.1 供电电压
分析正常运行电压幅值,设置基地220kV电压为223kV。
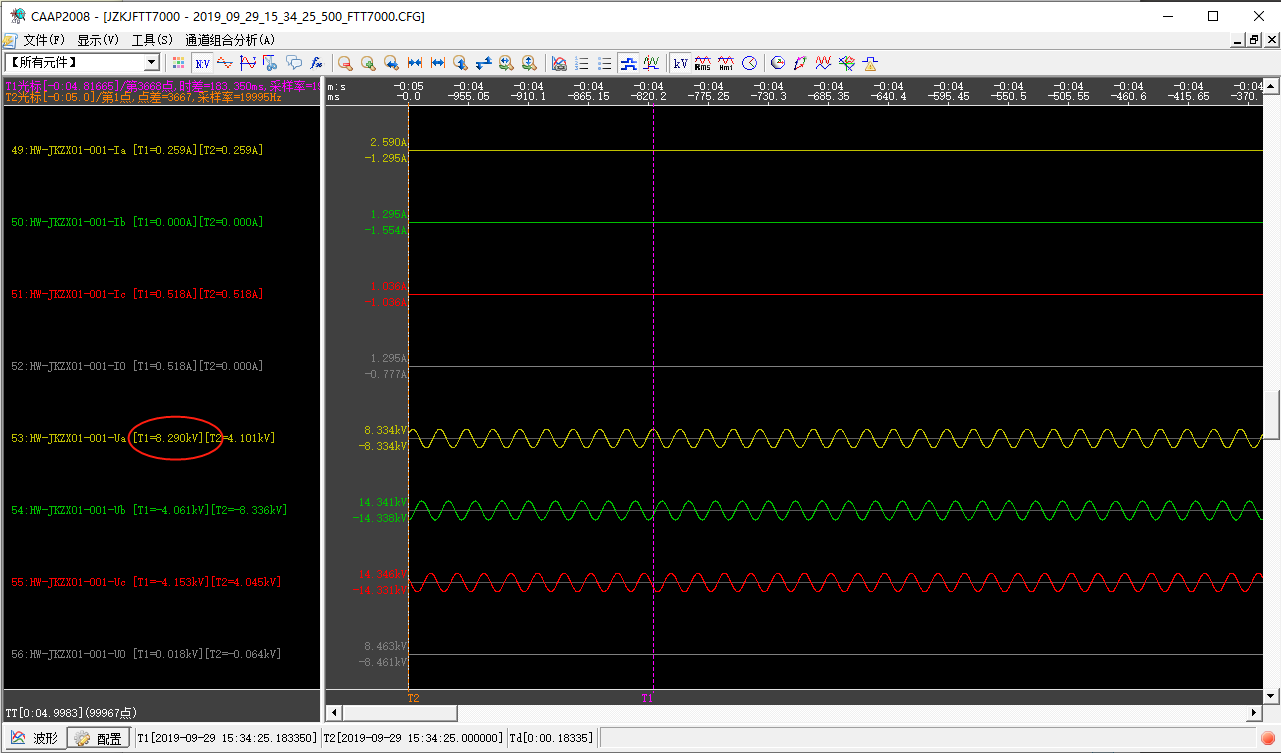
运行电压,基本一致。
1.2 设置变压器及开关站端口电容。
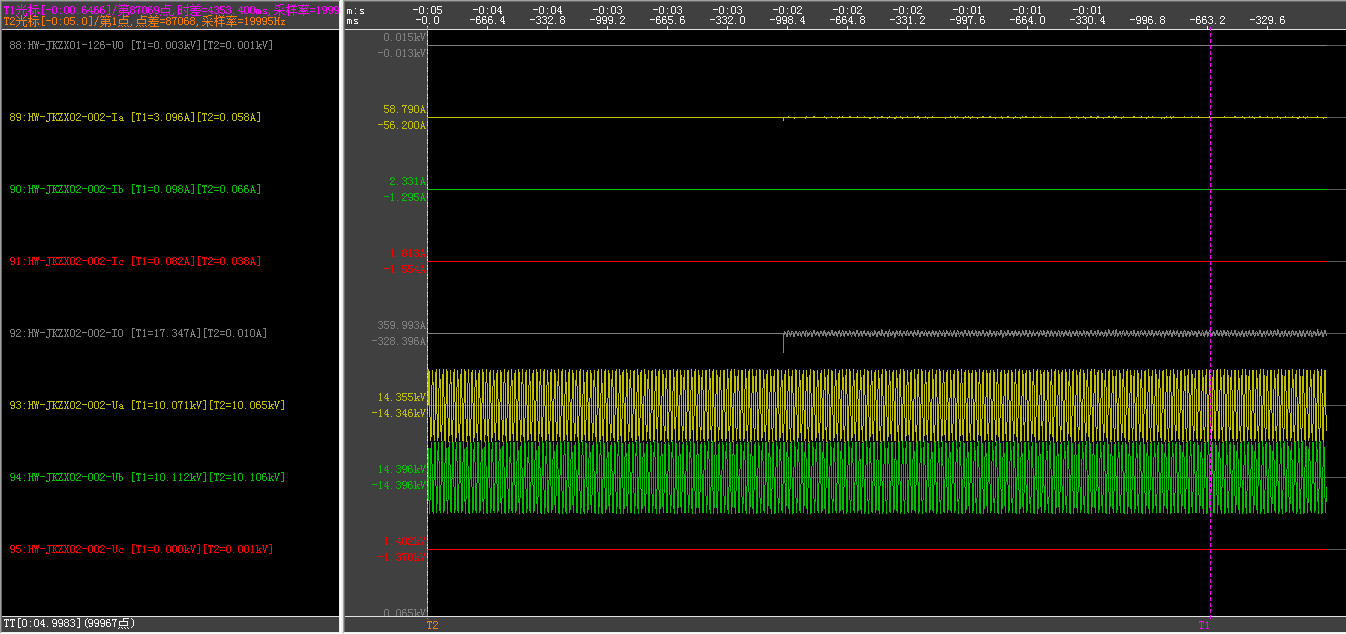
2条馈线发生单相接地故障后,本身在空载状态容流非常小,可以认为测定到的全部为背景容流,有效值为4.072A。
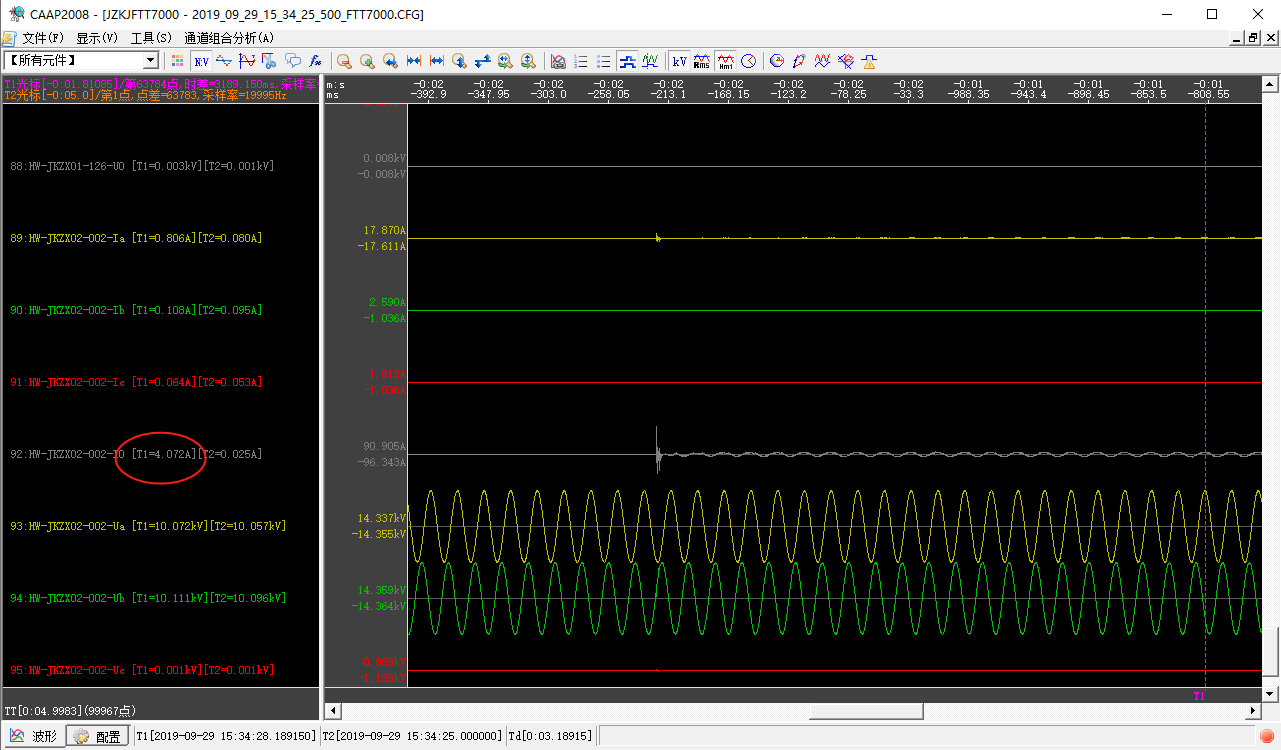
计算得到电容量为0.743-0.081=0.662uF。
仿真容流如图所示,基本一致。
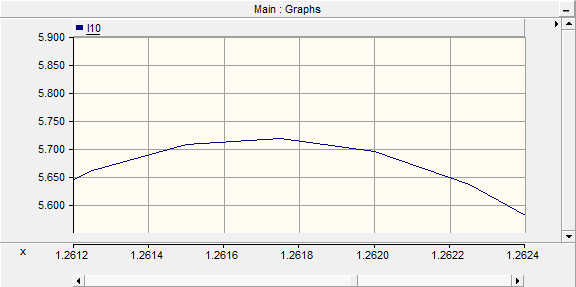
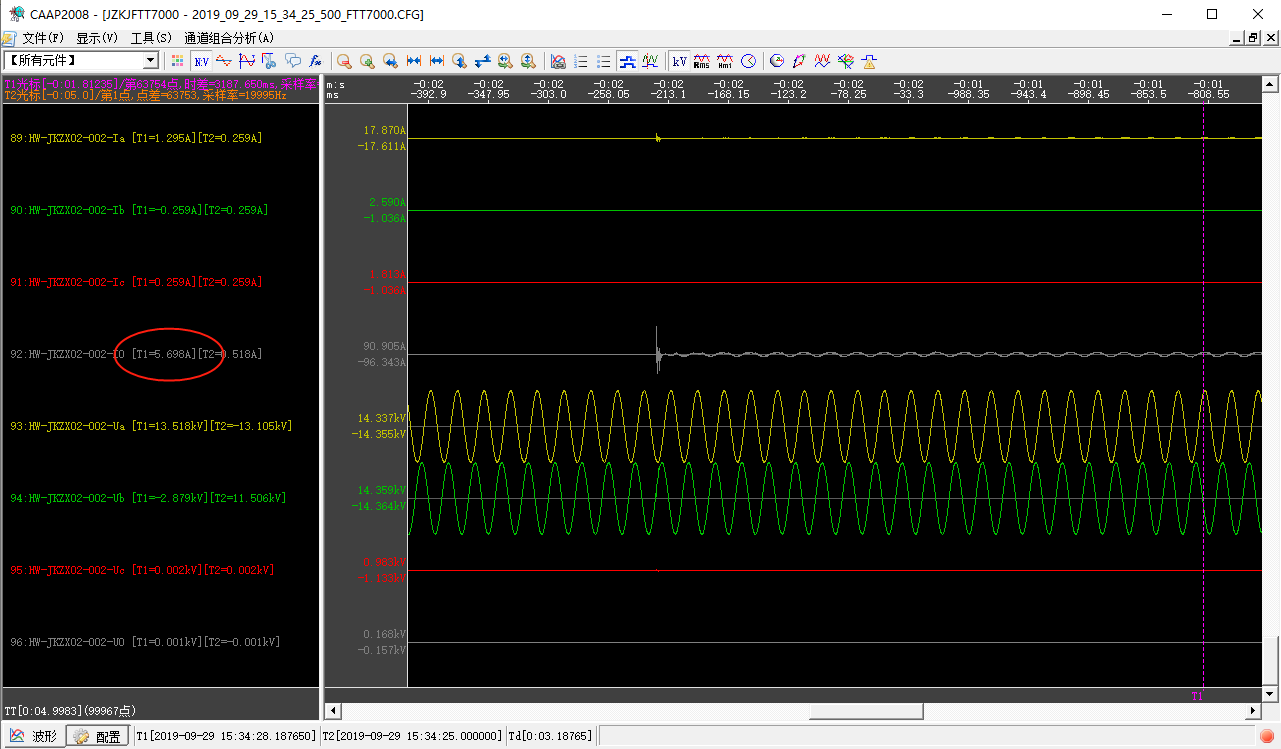
实测5.698A,仿真可的5.72A,基本相符。
1.3 考核场地网电阻
考虑故障相电压,故障后故障相电压为14V。
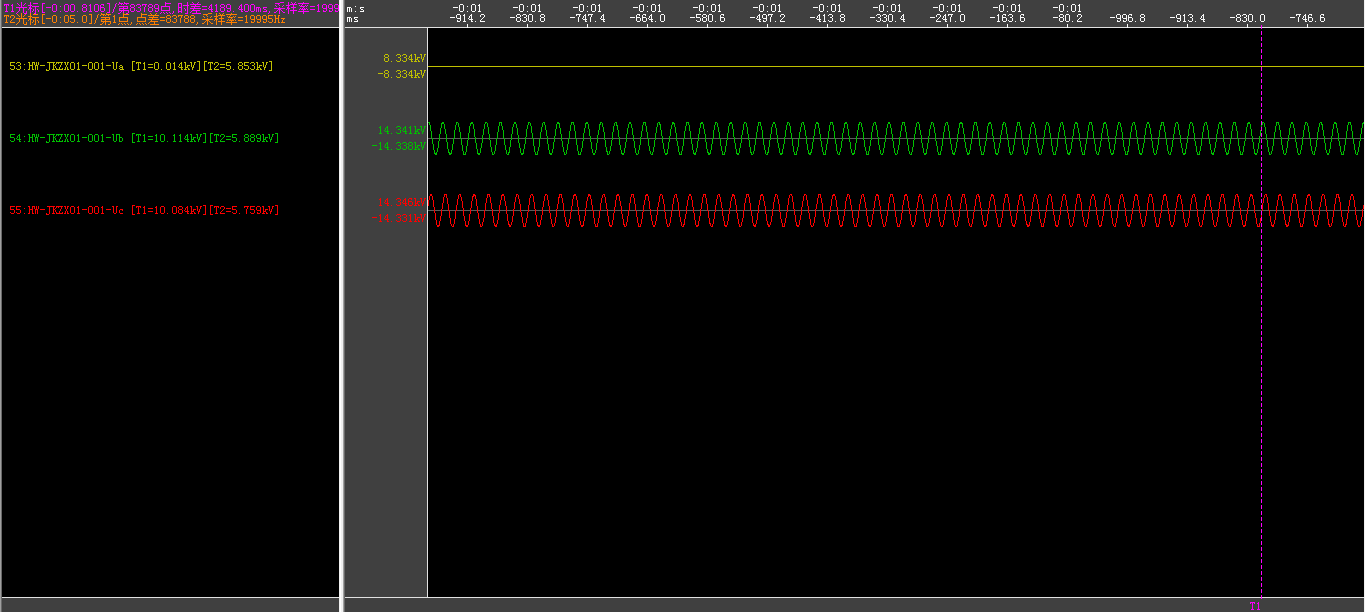
设置电阻为3.3Ω,仿真电压曲线如图。
基础模型设置完毕。
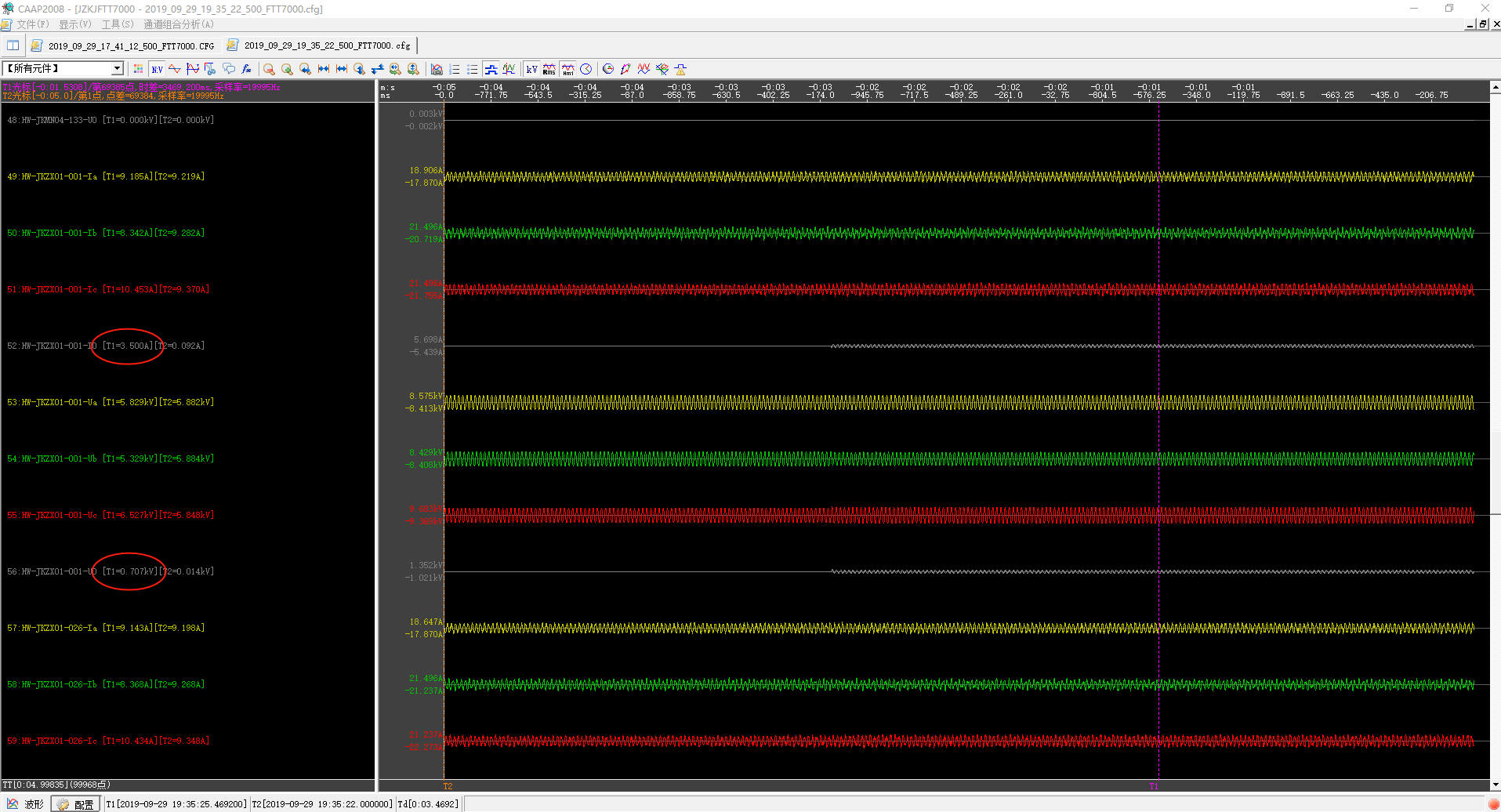
从另一个角度去计算地网故障过渡电阻。
记录馈线2的零序电流和故障相电压。
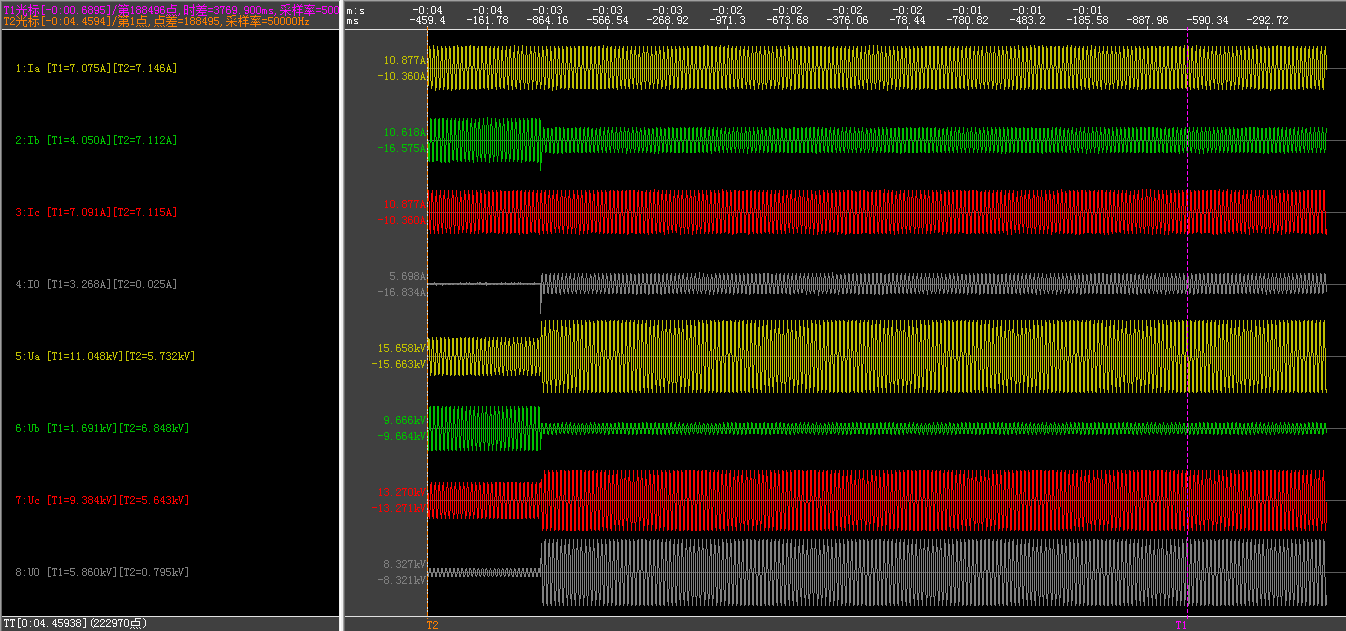
按照B相故障电压除以零序电流来计算B相接地阻抗,其值应等于接地电阻并联B相线路对地导纳。
\[R=1691(V)/ 3.268(A)=517.44(Ω)\]接地电阻为固定值500Ω。
也许散流电阻会随着阻抗值以及系统电流值而变化,那么就需要建立土地模型了。
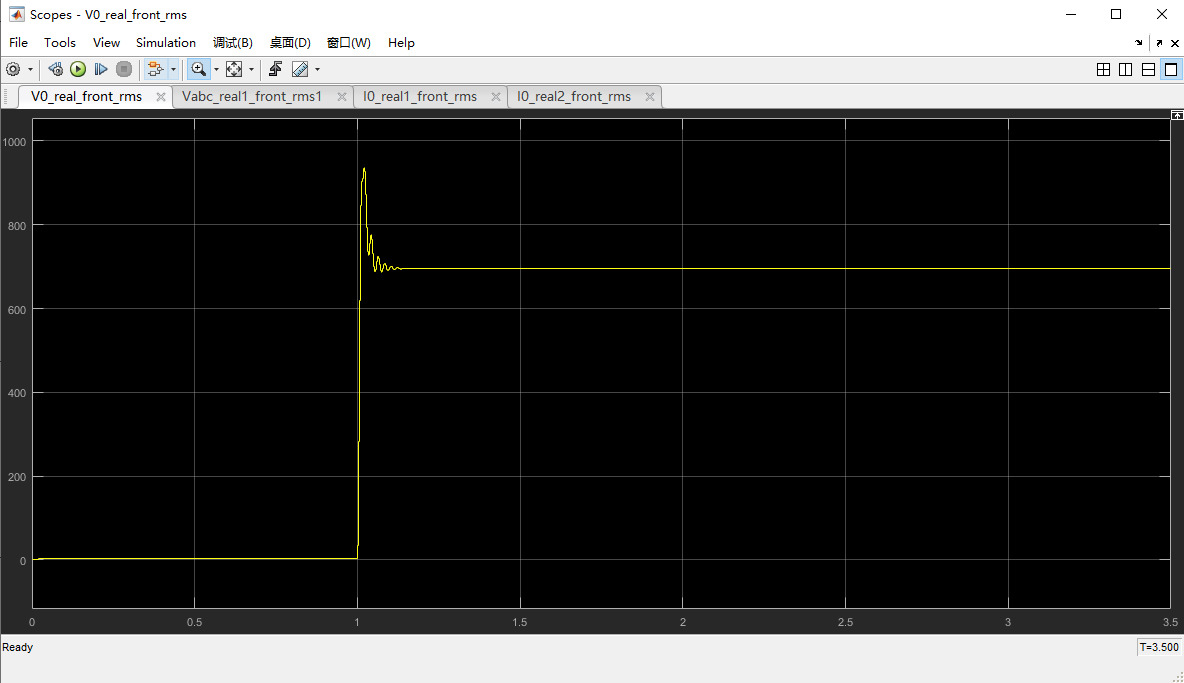
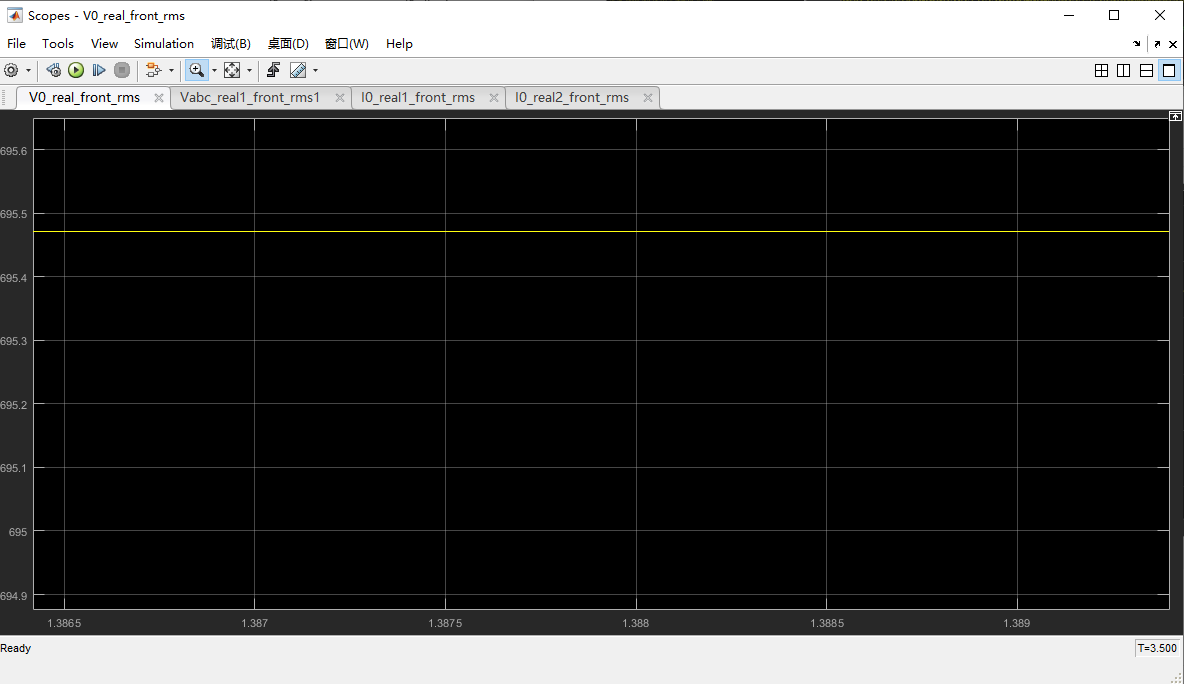
707V(实测)对应700V(仿真);
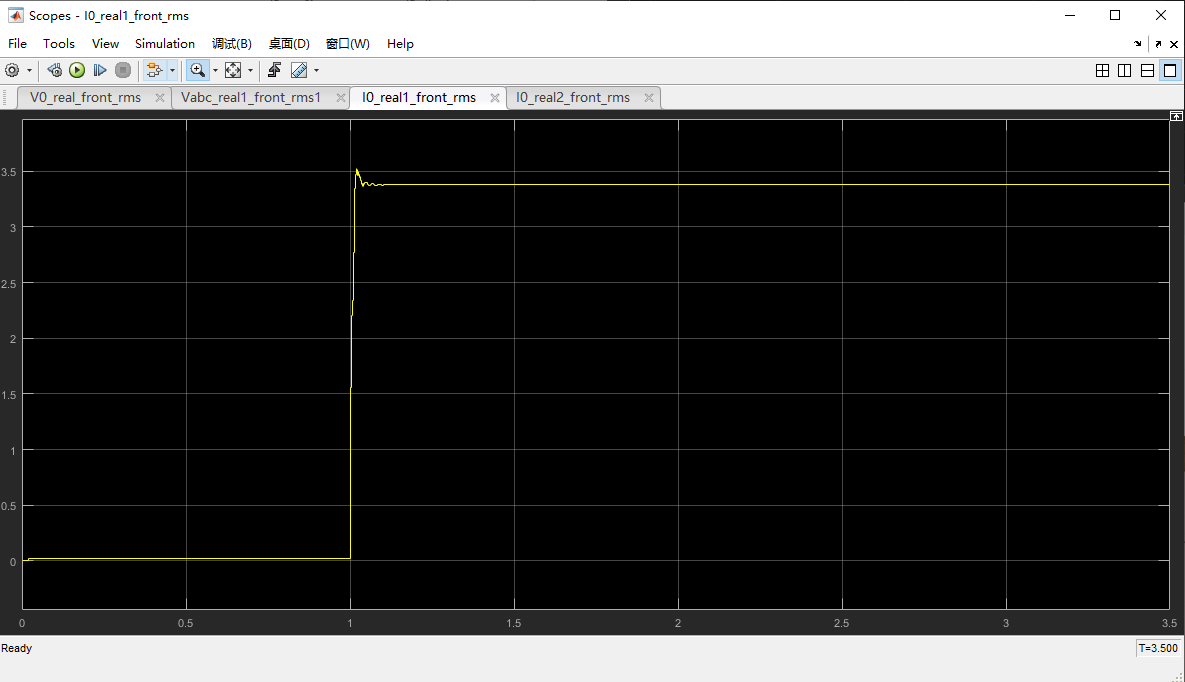
3.5A(实测)对应3.38A(仿真)。
2. 考虑对地导纳的中性点电压数学模型
2.1 数学模型
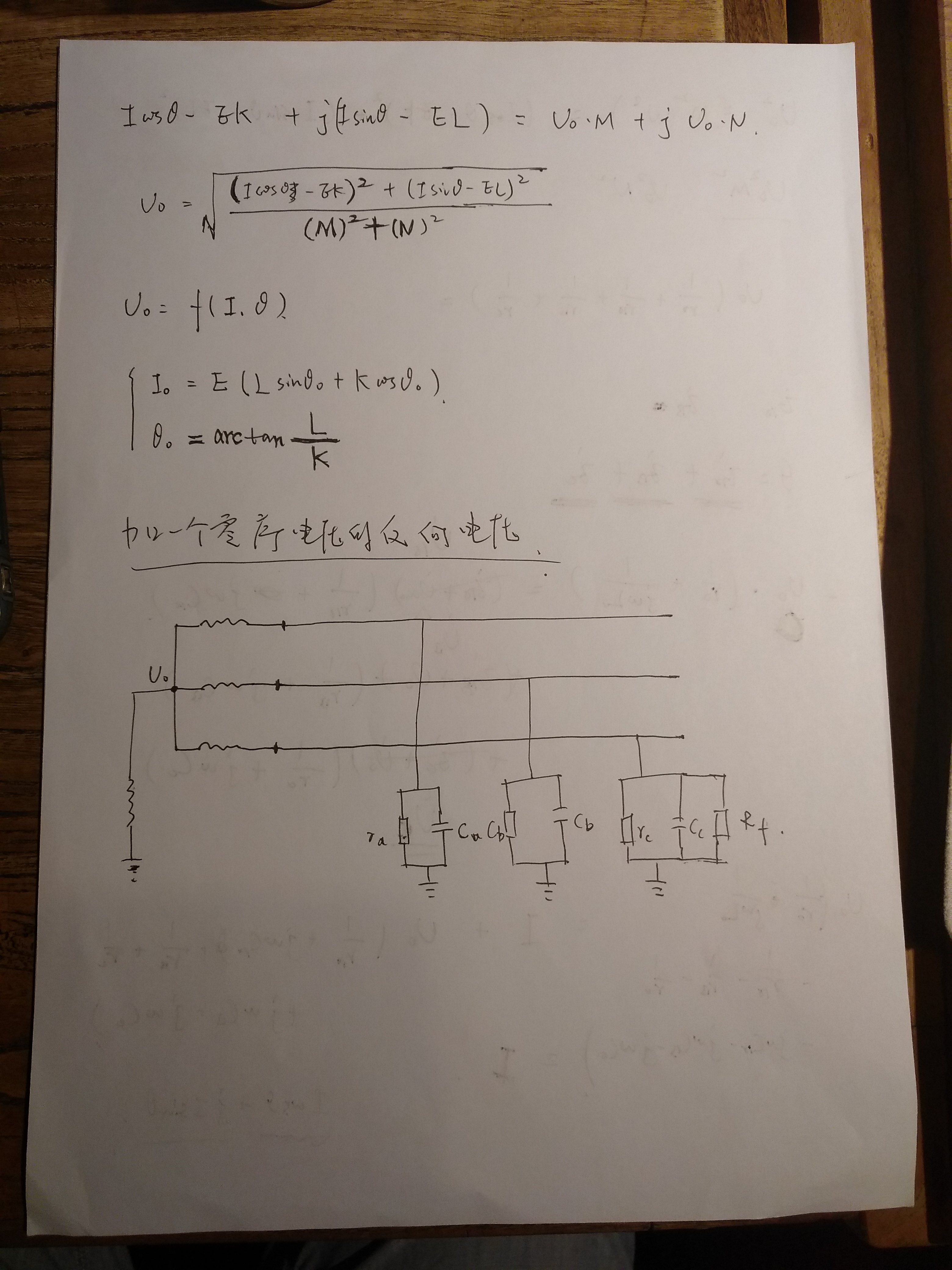


利用简化公式,得到接地电流的计算公式

2.2 数据分析
利用这组数据来计算一下,网架结构是4条馈线空载。

利用135和002的录波数据进行分析。
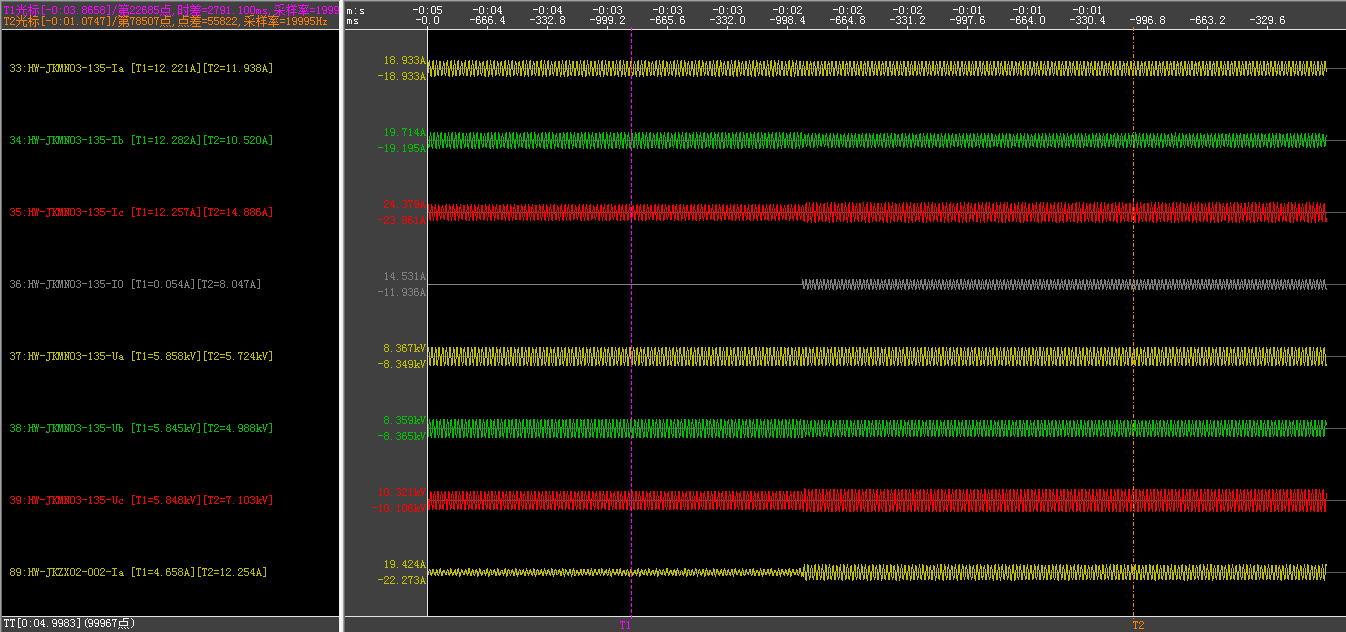

以上这组数据很奇怪,发生B相接地故障之后,B相电压降低,A相电压居然也降低了一点,大致保持不变,而C相电压升高,这不符合理论,考虑到架空1回线的感应电压,预计是感应电引起的。容性电流的测量数据也比较奇怪,为什么是这么大?是所有线路容性电流之和呢?
换一组更干净的数据进行计算。

试一试这组,1、2、3馈线,架空1、2馈线带小电容器,电缆1带5档电容器,故障电阻为500Ω。
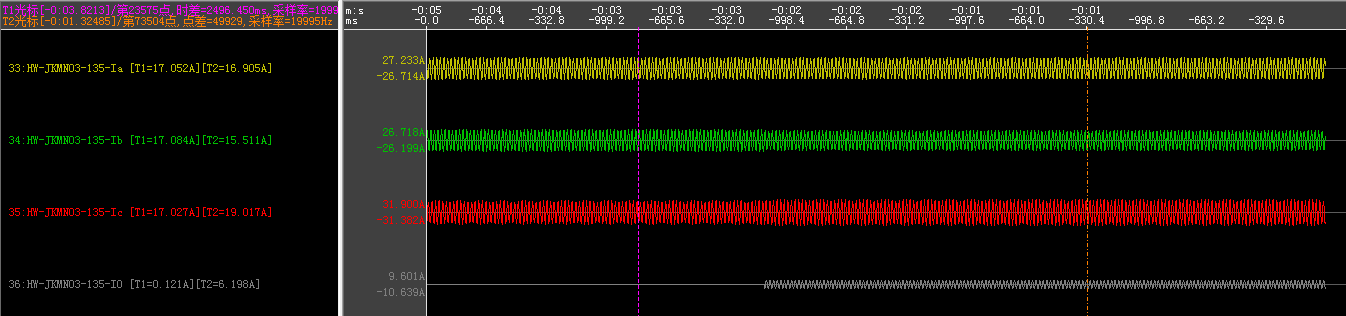
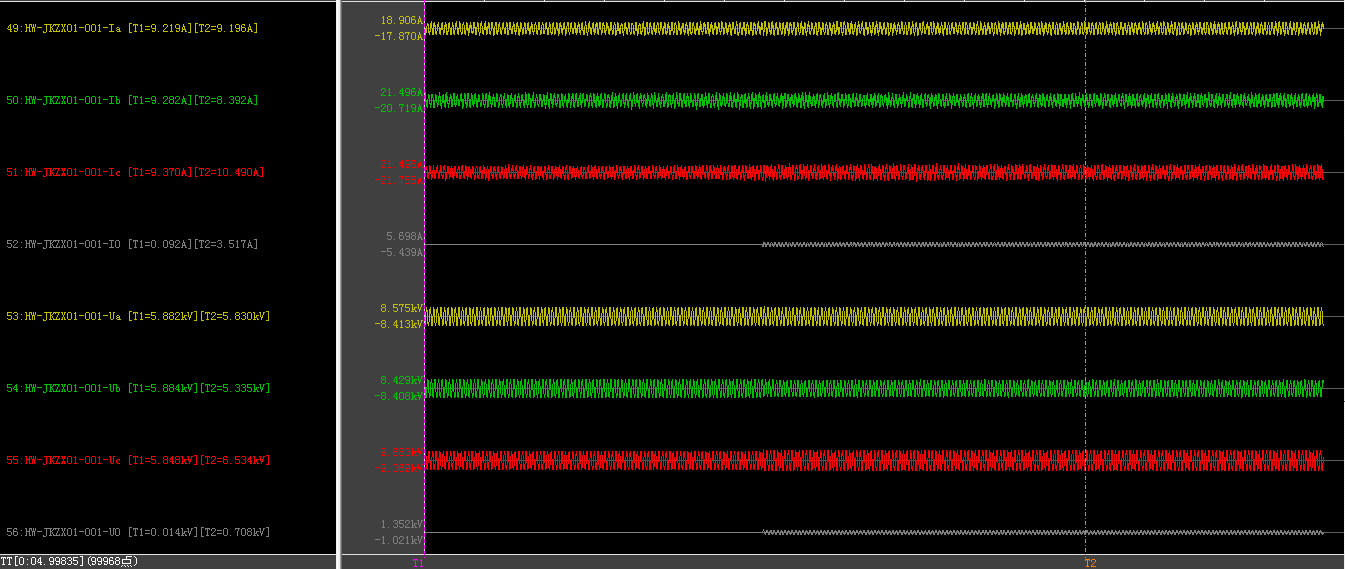
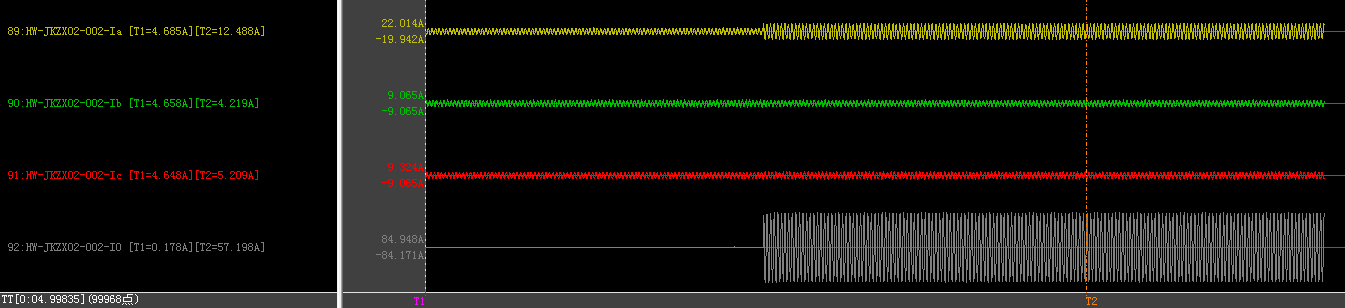
| 故障前 | 故障后 | ||||||
|---|---|---|---|---|---|---|---|
| $U_A$ | $U_B$ | $U_C$ | $U_0$ | $U_A$ | $U_B$ | $U_C$ | $U_0$ |
| 5884 | 5882 | 5851 | 14 | 5830 | 5335 | 6534 | 708 |
| $I_{1A}$ | $I_{1B}$ | $I_{1C}$ | $I_{10}$ | $I_{1A}$ | $I_{1B}$ | $I_{1C}$ | $I_{10}$ |
| 9.255 | 9.281 | 9.378 | 0.086 | 9.196 | 8.392 | 10.49 | 3.517 |
| $I_{2A}$ | $I_{2B}$ | $I_{2C}$ | $I_{20}$ | $I_{2A}$ | $I_{2B}$ | $I_{2C}$ | $I_{20}$ |
| 4.694 | 4.67 | 4.654 | 0.187 | 12.488 | 4.219 | 5.209 | 57.198 |
| $I_{3A}$ | $I_{3B}$ | $I_{3C}$ | $I_{30}$ | $I_{3A}$ | $I_{3B}$ | $I_{3C}$ | $I_{30}$ |
| 17.079 | 17.086 | 17.035 | 0.119 | 16.905 | 15.511 | 19.017 | 6.198 |
2.2.1 计算线路对地电容
首先计算线路对地电容,计算方法为在正常运行状态下,
计算每条馈线的电容,认为每条馈线的电容是对称的,可大约计算为:
馈线1 C=5uF;馈线2 C=2.5uF;馈线3 C=9.25uF。
则总并联馈线电容量为16.75uF。
\[r=\frac{3}{\sqrt{\frac{E^{2}}{U_{0}^{2} \cdot r_{f}^{2}}-9 \omega^{2} C^{2}}-\frac{1}{r_{f}}}\]按照上面手写的公式进行计算,计算得总的并联对地电阻r=935Ω。
2.2.2 计算接地阻抗公式
计算接地电阻公式得:
\[\left(9+9 \omega^{2} c^{2} r^{2}\right) r_{f}^{2}+6 r \cdot r_{f}+r^{2}+\frac{E^{2}}{U_{0}^{2}}=0\]解这样一个方程,其有解条件为:
\[\left(1-\omega^{2} c^{2} r^{2}\right) \frac{E^{2}}{U_{0}^{2}}-\omega^{2} c^{2} r^{2} \cdot r^{2} \geqslant 0\]2.2.3 找另一组电容量的进行计算

1、2、3馈线带3+4档电容器。
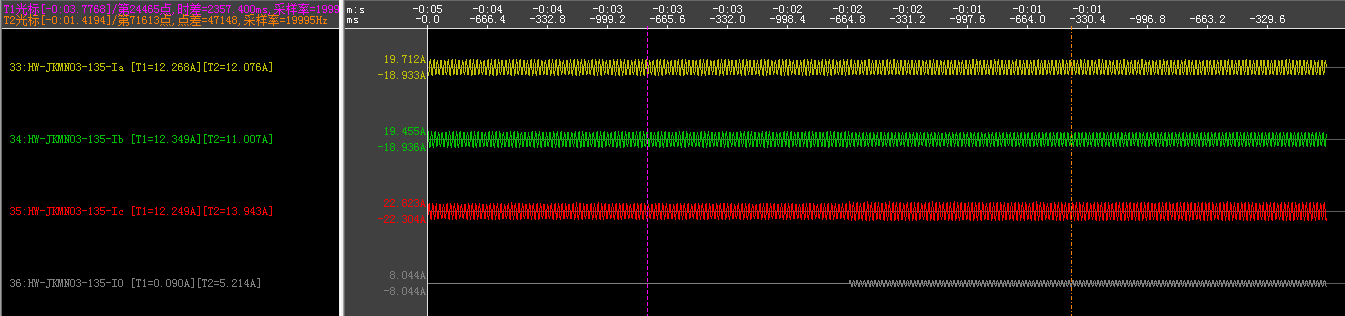
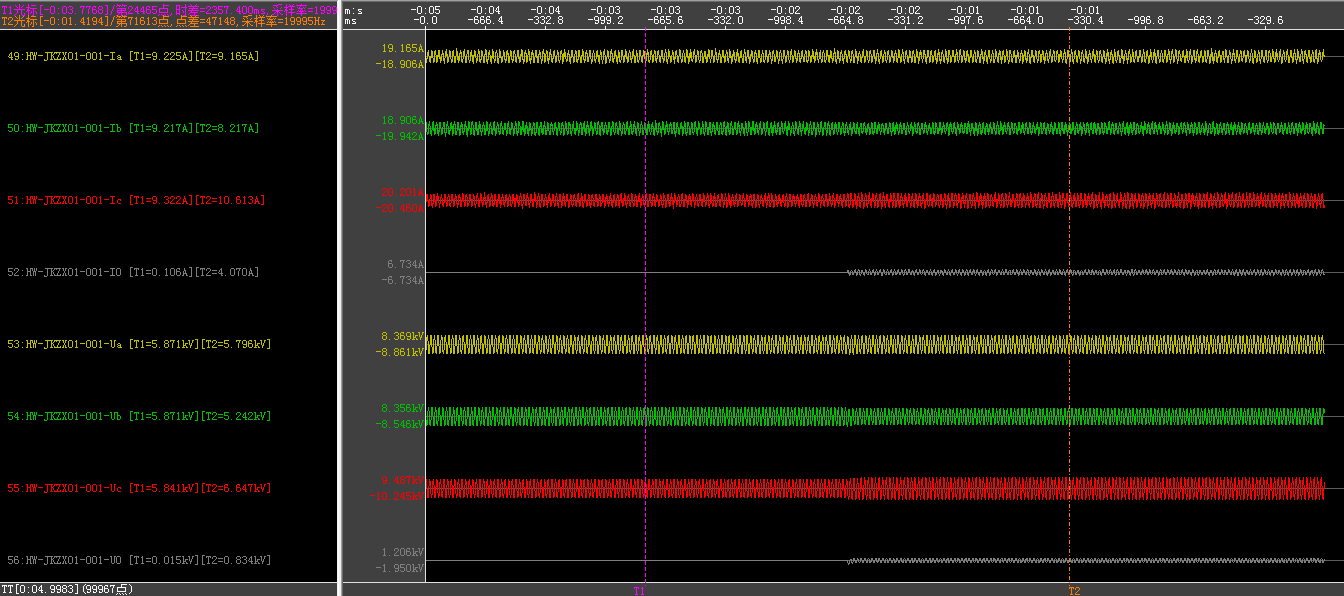
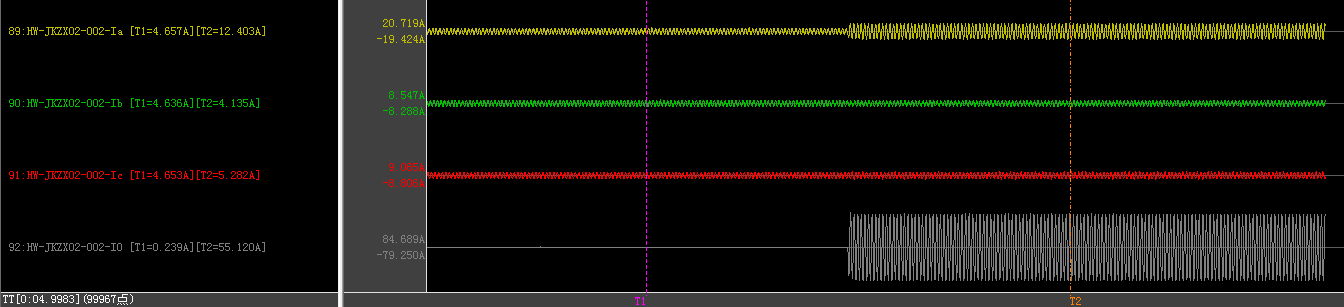
计算馈线3的电容量C3=6.7uF
则总的每相电容量可近似看做C=14.2uF
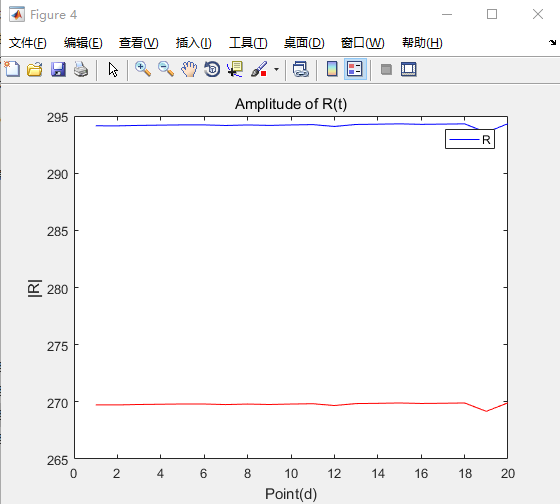
对地电导不能简单套用之前的计算结果,因为很可能电容的自放电电阻会串进回路中,从而导致不同网架结构及电容档位下,对地导纳的不准确,再换一组试一下。
2.2.4 6档电容,和计算出940欧姆电阻组只有电容器组别不同
总电容量
馈线1 C=5uF;馈线2 C=2.5uF;馈线3 C=18.358uF。
则总并联馈线电容量为25.858uF。
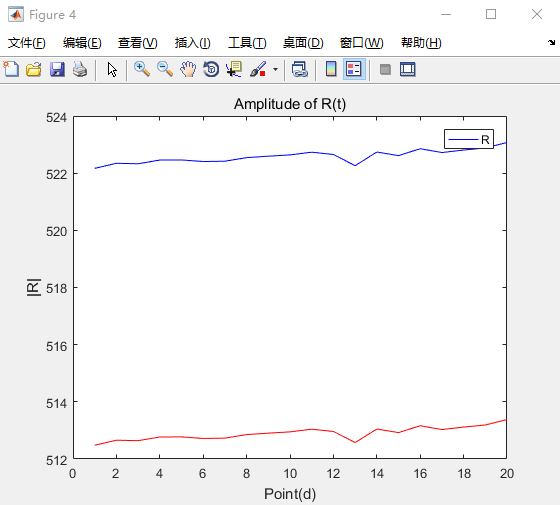
基本接近。
那么是否可以认为,之前3+4档不准确是因为多并进了一组电容器的自放电电阻,导致总体对地电导增加呢?那么现在如何准确测量对地电导就是解决这个问题的最终方案了。
2.2.4.7 1000欧姆电阻,只带线路电容器
按照线路对地电阻940欧姆进行辨识,辨识电阻差20欧姆,可接受。
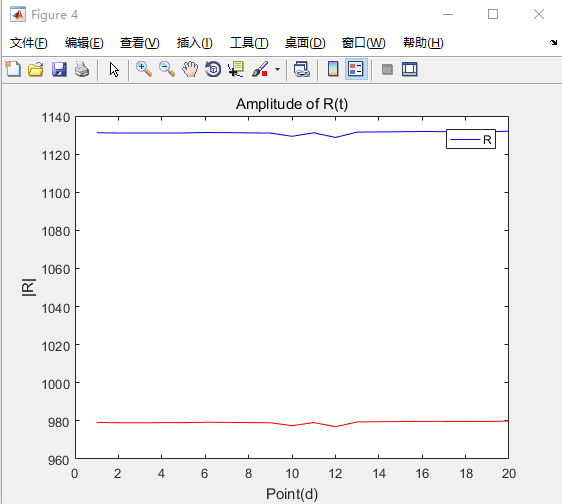
2.3 电弧的辨识
利用数据:两组小电容都带上第一次
相电势及零序电压曲线。
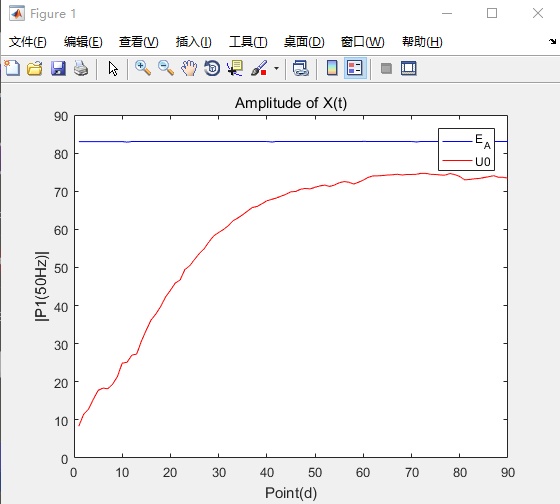
电阻值的变化曲线如图所示
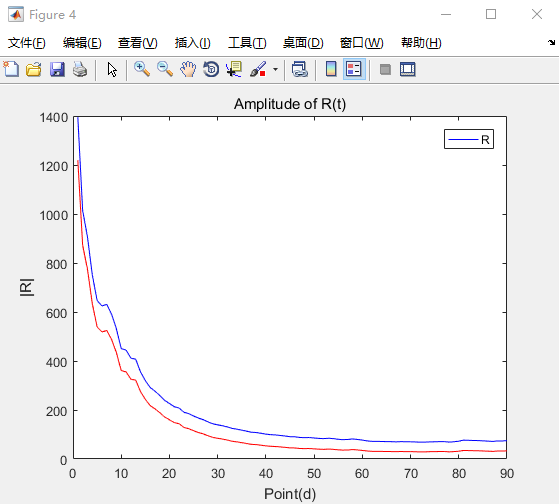
可以看出,随着电弧发展,电阻是逐渐变小的。但可以根据不同组数据推得,放电绝缘恢复后,绝缘强度会加大。
建模中需用到可控电流源