10. S函数
10.1 概述
作者分析,整个Simulink引擎调用通用库的模块时候使用的方法应该和S函数差不多。
10.2 S函数的类型
类型实际上可以分成2种,一种是语言类型,最主要的有M语言和C语言。支持功能多少分为Level1和Level2。M语言能实现的功能少,但相对简单,C Mex S函数能实现非常多的功能。Level1能实现单输入和单输出,目前已不建议使用,应使用Level2函数。
C Mex S函数有以下几个优点
- 实现功能多
- 仿真速度快
- 可与外部设备进行交互
- 可以通过Matlab为设备生成C代码
10.3 S函数的要素
S函数的原理无论哪种语言,都是一样的,一个模块包括输入、输出以及模型内部变量,以及一个时间变量。
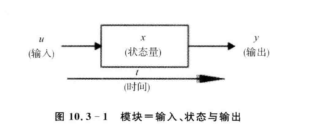
状态量x:状态量为模块内部的计算量或缓存量。所谓状态量,根据系统性质分为连续系统中的微分量和离散系统中的差分量。

10.4 S函数的组成及执行顺序
一个S函数有几个子方法构成,表征了S函数甚至整个Simulink引擎的工作过程。这些子方法包括模块初始化、采样时刻计算、模块输出的计算方法,模块离散状态量的更新方法、连续状态变量的微分方法和仿真结束前的终止方法等。
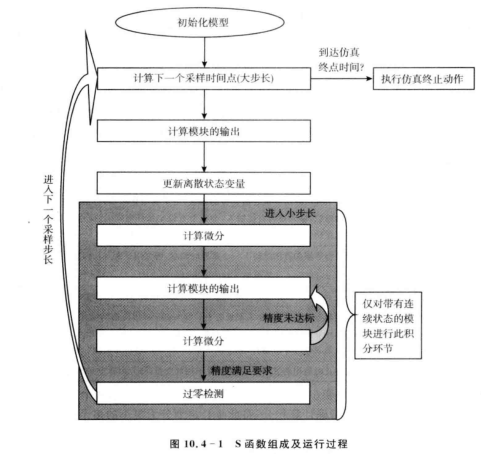
采样时间:即采样间隔。对于Simulink模型来说,解算器中的一个步长决定了整个模型最小的采样时间间隔,模型中的模块的步长,可以设置-1集成系统或父层模块的采样时间,也可以设置明确的数字决定执行间隔,但是此时这个间隔应该是系统采样时间间隔的整数倍。采样时间也可以是inf,表示不进行采样,即使常数。对于连续模块,设置采样时间为0。
运行顺序优先度:对于有输入/输出的模块来说,当输入/输出是直接馈入时,输入/输出需要再同一个采样时刻计算完毕,那么要求输入值准备好之后,才能进行输出值的计算。这样的模块必然依赖于连线的前一个模块的输出。对于输入/输出之间不是直接馈入的模块,输出值与状态值相关,与当前输入值无关,可以先行根据状态值计算出输出值,再处理输入值以更新状态值。对于没有输入/输出的模块,它本身不依赖前序模块,也不是后续模块的依赖,其计算顺序则是另外一种情况。模块的执行顺序也收到模块输入/输出以及直接馈入的影响。
S函数的执行顺序:
- 模型初始化之后,如果是采样时间变化(下称变采样时间)的模块,需要在每个采样时刻计算出下一个采样时刻;
- 如果不是变采样时间的模块,则无需计算下一个采样时刻,直接计算模块的输出Outputs。
- 紧接着再进行更新子方法(Update)执行,主要用于离散状态变量等的更新。
- 接下来计算积分环节(integration),由多个子环节构成、主要用于处理连续状态的计算和更新及非采样过零检测的实施。
- 对于存在连续状态的S函数,Simulink将会以小步长进行输出方法Outputs与微分计算方法derivative的调用。
- 对于非采样过零检测,Simulink将会调用输出方法Outputs及过零检测子方法zero-crossings以精确定位过零的位置。
| 子方法 | 作用 |
|---|---|
| 初始化 | 在第一个采样时间的仿真之前运行的函数,用来初始化模块,包括设定输入/输出端口的个数和维数,输入是否直接馈入,参数个数设定采样时间,当使用工作向量时还需要为其分配存储空间 |
| 下一个采样点时间计算 | 根据模型解算器的算法求得下一个采样时刻点,通常用于变步长模块 |
| 输出函数计算 | 在每一个major step计算模型所有的输出口的输出值 |
| 离散状态更新 | 在每一个major step都进行一次离散状态的更新计算,在输出函数之后 |
| 积分计算 | 如果模型具有连续状态,才采取此方法,将major step分隔为数个minor step,在每一个minor step里进行一次输出函数与积分计算。积分计算主要用来更新连续状态。当模型存在非采样过零检测时,还会在minor step中进行过零检测 |
| 模型终止 | 当仿真终止时调用的子函数,用于清除不用的变量,释放内存空间等动作 |
minor step与major step是变步长解算器相关的知识点,后者表示连个采样点之间的步长;前者表示major step内为了精确计算积分,将次步长再划分为更小的多个步长。
10.5 编写S-Function
Level1 M : 支持简单的MATLAB接口及少数S函数API。
Level2 M : 支持扩展S函数API及代码生成功能,使用场合更加广泛。
C MEX 提供更灵活的变成方式,既可手写C代码也可以调用既存的C/C++代码或Fortran代码。要求掌握很多C MEX S函数 API 用法及TLC代码编写方法,才能够定制具有代码生成功能的C MEX S-Function。
10.5.1 Level1 M S-Function
函数原型为:[sys,x0,str,ts]=f(t,x,u,flag,p1,p2,…),其中f是S函数的函数名。Simulink会在仿真过程的每个步长内多次调用f。flag的值随着仿真过程自动变化,其值对应的S函数子方法如表所示。
| flag值 | Level1 M S函数子方法名 | 说明 |
|---|---|---|
| 0 | mdlInitializeSizes | 定义S函数的基本属性,如输入/输出维数、连续/离散状态变量个数、采样时间,以及输入是否为直接馈入 |
| 1 | mdlDerivatives | 连续状态变量的微分函数,这里通常通过给定的微分计算表达式,通过积分计算得到状态变量的值 |
| 2 | mdlUpdate | 更新离散状态变量 |
| 3 | mdlOutputs | 计算S函数的输出 |
| 4 | mdlGetTimeOfNextVarHit | 尽在变离散采样时间情况下(ts = [-2 0]时)使用,用于计算下一个采样时刻的绝对时间,若模块不是变步长此函数不会执行 |
| 9 | mdlTerminate | 在仿真结束时执行一些必要的动作,如清除临时变量,或显示提示信息等 |
注:模块是否直接馈入有一个简单的判断方法,就是查看mdlOutputs和mdlGetTimeOfNextVarHit两个子方法中有没有用到输入u。如果用到了,这个输入端口的直接馈入direct feedthrough就必须设置为1。
Level 1 M S函数的采样时间ts,适用于Level 2 M S函数和C MEX S 函数。有一个包含两个元素的数组[m,n]表示,m为模块的采样时间周期,或连续或离散或继承父层模型的采样时间,表示每隔多长时间采样一次;n为采样时间的偏移量,表示与采样时间周期所表示的时刻点的偏差时间。常见的设置见表。
| 采样时间表示 | 意义 |
|---|---|
| [0 0] | 连续采样时间 |
| [-1 0] | 继承S函数输入信号或父层模型的采样时间 |
| [0.5 0.1] | 离散采样时间,从0.1秒开始每0.5s采样一次 |
一个S函数可以同时存在多个采样速率,可以通过设置多维数组来实现多个速率采样时间的配置,如[0.25 0; 1 0.1],在这个S函数中,采样时刻为[0 0.1 0.25 0.5 0.75 1 1.1…]。
例子,通过Level1 M S函数来实现这个方程。

可以很容易得知:
A = [-0.5572 -0.7814;0.7814 0]; B = [1 -1; 0 2]; C = [1.9691 6.4483]。
为S函数设置3个参数,用来传递矩阵A、B、C到S函数中,在Update和Output子方法中分别使用其中部分参数,Update的参数列表中仅需要使用A、B,Outputs子方法中仅需要使用C。Level1 M S函数构成的模块最多仅支持单个输入口,单个输出口。所以输入口的维数要设置为2.状态变量采用离散状态变量,在S函数中按列排序。然后需要判断直接馈入,由于输出y由状态变量x决定,不由输入u决定,所以不存在直接馈入。根据分析,可以编写代码如下。
function [sys,x0,str,ts,simStateCompliance] = sfun_state01(t,x,u,flag,A,B,C)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u,A,B);
case 3,
sys=mdlOutputs(t,x,u,C);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 2;
sizes.NumOutputs = 1;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0 0]';
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
function sys=mdlUpdate(t,x,u,A,B)
sys = A * x + B * u;
function sys=mdlOutputs(t,x,u)
sys = C * x;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];
% end mdlTerminate
在S函数对话框中填入参数。
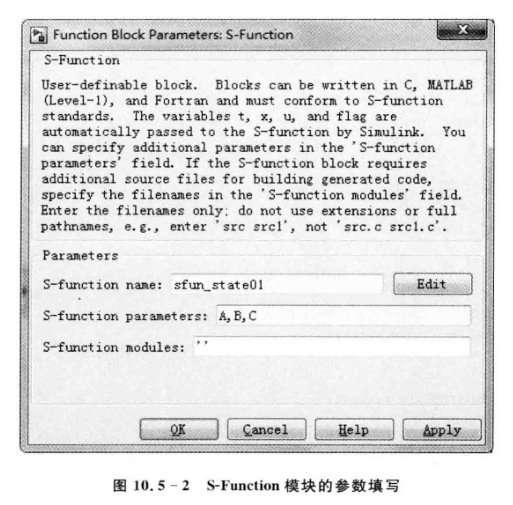
不建议使用全局变量的原因
- 全局变量会破坏模块化设计,增加模块之间的耦合性。当系统复杂之后,依赖全局变量过多,会造成难以管理的混乱局面。建议尽量不适用全局变量,以养成好习惯。
- 不出现多次的global声明,代码看起来清爽简约并充分发挥了S函数的作用。
离散变量通过明确的表达式来进行值的更新。而连续状态下,mdlDerivatives子方法的计算方式有所不同。mdlDerivatives子方法中编写的表达式计算出来的值会自动进行一次积分,得到的值才更新到连续状态变量中去,作为下一个采样时刻的连续状态值进行下一次的计算。积分的S函数代码为:
function [sys,x0,str,ts,simStateCompliance] = sfun_hyo(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 1;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = u;
function sys=mdlUpdate(t,x,u,A,B)
sys = [];
function sys=mdlOutputs(t,x,u)
sys = x;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];
% end mdlTerminate
这个函数中,初始化输入/输出端口为一维,一个初始值为0的连续状态变量,连续采样时间,输入端口没有直接馈入。
多然由于对S函数运行原理、参数传递、直接馈入等方法或概念不太熟悉,导致编写S函数时遇到各种错误。
- flag = 3时仿真出错,往往由于输出维数配置不当或使用了输入u但是没有在初始化时将输入端口配置为直接馈入。
- 参数未定义,命名S函数参数列表中设置了参数却没有添加到每个子方法的参数列表中导致子方法中参数未定义错误。
10.5.2 Level2 M S-Function
Level 2 M S函数调用模块如图所示。
Level 2 M S函数使得用户能够使用MATLAB语言来编写支持多个输入/输出端口的自定义模块,并且每个端口都能够支持包括矩阵在内的Simulink支持的所有数据类型。
Level 2 M S函数提供了一系列API设置模块属性和定义各个子方法,其中Setup和Outputs两个方法是必不可少的。
1.Setup子方法
Setup子方法是Level 2 M S函数整体中唯一调用的语句,对模块的属性和其他子方法进行初始化,Setup子方法类似Level 1 M S函数中mdlInitializeSizes子方法的功能,并且相比之下功能更强大。在Setup中可以设置多输入多输出,并且每个输出的端口信号的维数可以是标量或矩阵以及可变维数,S函数的其他子方法也是通过Setup子方法进行注册的,可以成为Level 2 M S函数的根本。Setup子方法实现以下功能:
- 设定模块输入输出端口的个数;
- 设定每一个端口的数据类型、数据维数、实数复数性和采样时间等;
- 规定模块的采样时间;
- 设定S函数参数的个数;
- 注册S函数的子方法(将子方法函数的句柄传递到实时对象的RegBlockMethod函数的对应属性中)。
Setup子方法的参数为block,是一个Level 2 M S函数的实时对象,包括了一些属性和方法。其属性成员如表
Level 2 M S函数实时对象的属性列表
| 实时对象属性成员 | 说明 | 实时对象属性成员 | 说明 |
|---|---|---|---|
| NumDialogPrms | 模块GUI参数个数 | NumContStates | 连续状态变量数目 |
| NumInputPorts | 输入端口数 | NumDworkDiscStates | 离散状态变量个数 |
| NumOutputPorts | 输出端口数 | NumRuntimePrms | 运行时参数个数 |
| BlockHandle | 模块句柄,只读 | SampleTimes | 产生输出的模块的采样时间 |
| CurrentTime | 当前仿真时间,只读 | NumDworks | 离散工作向量个数 |
通过block变量的点操作符来访问上表中属性并且可以直接使用等号赋值:
block.NumDialogPrms = 0;
模块的输入/输出端口又包含自己的属性,其中常用的属性列表如表所示。
Level 2 M S函数端口的属性列表
| 端口属性名 | 说明 |
|---|---|
| Dimensions | 端口数据维数 |
| DatatypeID/Datatype | 端口数据类型,可通过ID号制定也可以直接制定数据类型名 |
| Complexity | 端口数据是否为复数 |
| DirectFeedthrough | 端口数据是否直接馈入 |
| DimensioinsMode | 端口维数是固定或可变(fixed/variable) |
当模块中存在多个端口时,需要对每一个端口进行属性的设定,使用端口访问方法(InpuPort或OutputPort成员)及端口号索引(正整数)设定输入/输出端口,如:
block.InputPort(1).Dimensionis = 1;
Setup子方法中,出来能够通过block实时对象域操作符访问模块属性之余,还可以通过子方法获取模块对象的信息,可以调用的方法列表如表所列。
Level 2 M S 函数实时对象的方法列表
| 实时对象方法 | 说明 | 实时对象方法 | 说明 |
|---|---|---|---|
| ContStates | 获取模块的连续状态 | Dwork | 获取Dwork向量 |
| DataTypelsFixedPoint | 判断数据类型是否为固定点数 | FixedPointNumericType | 获取固定点数据类型属性 |
| DatatypeName | 获取数据类型的名称 | InputPort | 获取输入端口 |
| DatatypeSize | 获取数据类型大小 | OutputPort | 获取输出端口 |
| Derivatives | 获取连续状态的微分 | RuntimePrm | 获取运行时参数 |
| DialogPrm | 获取GUI中的参数 |
Setup子方法中还需要使用RegBlockMethod函数来注册S函数中需要用到的其他各个子方法,如表所列
其他子方法列表
| 子方法名 | 说明 |
|---|---|
| PostPropagationSetup | 设置工作向量机状态变量的函数(可选) |
| InitializeConditions | 在仿真开始时被调用的初始化函数(可选) |
| Start | 在模型运行仿真时调用一次,用来初始化状态变量和工作向量(可选) |
| Outputs | 在每个步长里计算模型输出 |
| Update | 在每个步长里更新离散状态变量的值(可选) |
| Derivatives | 在每个步长里更新连续状态变量的微分量(可选) |
| Terminate | 在仿真结束时调用,用来清除变量内存 |
表中“可选”表示不是必须存在于S函数中,根据需要进行选取。
下面例子,使用Setup子函数初始化一个带有1个参数、1个输入端口、1个输出端口的模块,输入/输出端口维数都为1,没有直接馈入;模块的采样时间为0.1s,注册4个子方法函数:DoPostPropSetup,InitConditions,Output和Update。
function msfuntmpl(block)
%MSFUNTMPL A Template for a MATLAB S-Function
% The MATLAB S-function is written as a MATLAB function with the
% same name as the S-function. Replace 'msfuntmpl' with the name
% of your S-function.
% Copyright 2003-2018 The MathWorks, Inc.
%
% The setup method is used to setup the basic attributes of the
% S-function such as ports, parameters, etc. Do not add any other
% calls to the main body of the function.
%设置方法用于设置S功能的基本属性,例如端口,参数等。请勿在功能主体上添加其他任何调用。
%
setup(block);%设置模块
%endfunction
% Function: setup ===================================================
% Abstract:
% Set up the S-function block's basic characteristics such as:%设定基础参数
% - Input ports%输入端口
% - Output ports%输出端口
% - Dialog parameters%对话参数
% - Options%选项
%
% Required : Yes
% C MEX counterpart: mdlInitializeSizes
%
function setup(block)
% Register the parameters.初始化对话框参数
block.NumDialogPrms = 1;%初始化三个S函数对话框参数
block.DialogPrmsTunable = {'Tunable','Nontunable','SimOnlyTunable'};%参数是否可变
% Register the number of ports.设置输入输出端口数
block.NumInputPorts = 1;
block.NumOutputPorts = 1;
% Set up the port properties to be inherited or dynamic.将端口属性设置为继承或动态。以指示输入和输出端口从模型继承其已编译属性(尺寸,数据类型,复杂度和采样模式)
block.SetPreCompInpPortInfoToDynamic;%设定输入端口属性为动态
block.SetPreCompOutPortInfoToDynamic;%设定输出端口属性为动态
% Override the input port properties.覆盖输入端口属性
block.InputPort(1).DatatypeID = 0; % double
block.InputPort(1).Complexity = 'Real';
% Override the output port properties.覆盖输出端口属性
block.OutputPort(1).DatatypeID = 0; % double
block.OutputPort(1).Complexity = 'Real';
% Hard-code certain port properties
block.InputPort(1).Dimensions = 1;
block.InputPort(1).DirectFeedthrough = false;
block.OutputPort(1).Dimensioins = 1;
% Set up the continuous states.设定具有连续状态变量个数
% block.NumContStates = 1;
% Register the sample times.设定采样时间
% [0 offset] : Continuous sample time连续的采样时间
% [positive_num offset] : Discrete sample time离散的采样时间
%
% [-1, 0] : Inherited sample time继承的采样时间
% [-2, 0] : Variable sample time可变采样时间
block.SampleTimes = [0.1 0];%设定上面的采样时间,设置为[-1 0]即制定S函数具有继承的采样时间
% -----------------------------------------------------------------
% Register the methods called during update diagram/compilation.
% -----------------------------------------------------------------
%
% PostPropagationSetup:
% Functionality : Set up the work areas and the state variables. You can
% also register run-time methods here.
% C MEX counterpart: mdlSetWorkWidths
%
block.RegBlockMethod('PostPropagationSetup', @DoPostPropSetup);
%
% InitializeConditions:
% Functionality : Call to initialize the state and the work
% area values.
% C MEX counterpart: mdlInitializeConditions
%
block.RegBlockMethod('InitializeConditions', @InitializeConditions);
%
% Outputs:
% Functionality : Call to generate the block outputs during a
% simulation step.
% C MEX counterpart: mdlOutputs
%
block.RegBlockMethod('Outputs', @Outputs);
%
% Update:
% Functionality : Call to update the discrete states
% during a simulation step.
% C MEX counterpart: mdlUpdate
%
block.RegBlockMethod('Update', @Update);
%
% Derivatives:
% Functionality : Call to update the derivatives of the
% continuous states during a simulation step.
% C MEX counterpart: mdlDerivatives
%
block.RegBlockMethod('Derivatives', @Derivatives);
2.PostPropagationSetup子方法
PostPropagationSetup子方法是用来初始化Dwork工作向量的方法,规定Dwork向量的个数及每个向量的维数、数据类型、离散状态变量的名字和虚实性,以及是否作为离散状态变量使用。
DWork向量时SImulink分配给模型中每个S函数实例的存储空间块。当不同S函数模块之间需要通过全局变量或者静态变量进行数据交互时,必须在S函数模块存在多个拷贝时,每一个模块中全局变量所使用的空间都需要十分小心的分配、修改和释放,特别是在使用C语言进行函数编写时更要进深。因为一旦管理不慎,可能会造成S函数的一个实例的数据被另一个实例的数据所覆盖,导致计算出错并最终使得仿真失败。使用Dwork向量可以有效防止这些情况发生,可重复性(reentrancy)有效地保证了S函数多个实例的可跟踪性,当S函数中使用Dwork向量时,这个S函数的实例就具备了可重入性,Simulink为这个S函数的每一个实例分别管理数据。
Dwork向量既可以作为全局变量在S函数模块之间传递数据,也可以作为某个S函数内部离散状态变量来使用。举一个例子说明在PostPropagationSetup子方法中使用Dwork向量作为离散状态变量的使用方法。在下面代码中,DoPostPropSetup函数作为PostPropagationSetup子方法的回调函数,程序中定义了一个Dwork向量,命名为x0,维数为1,数据类型是double型实数,此Dwork向量作为离散状态使用。
function DoPostPropSetup(block)
block.NumDworks = 1;
block.Dwork(1).Name = 'x0';
block.Dwork(1).Dimensions = 1;
block.Dwork(1).DatatypeID = 0; % double
block.Dwork(1).Complexity = 'Real'; % real
block.Dwork(1).UsedAsDiscState = true;
% Register all tunable parameters as runtime parameters.
block.AutoRegRuntimePrms;
%endfunction
Dwork向量的数据类型,通常使用DatatypeID来表示,每一个数据类型对应一个整数。
Level 2 M S函数实时对象支持的数据类型列表
| 数据类型 | 代表数据类型的整数 | 数据类型 | 代表数据类型的整数 |
|---|---|---|---|
| inherited | -1 | int16 | 4 |
| double | 0 | uint16 | 5 |
| single | 1 | int32 | 6 |
| int8 | 2 | uint32 | 7 |
| uint8 | 3 | boolean或定点类型 | 8 |
上例中定义Dwork向量数据类型为double,故使用整数0代表。
3. InitializeConditions/Start子方法
InitializeConditions子方法可以用来初始化状态变量或DWork工作向量的值,下面例子中InitConditions函数作为InitializeConditions子方法的回调函数,其内容是通过S函数对话框获取DWork的初始值,连续状态变量的值初始化为1.0。
function InitializeConditions(block)
block.Dwork(1).Data = block.DialogPrm(1).Data;
block.ContStates.Data = 1;
%endfunction
Start子方法跟initializeConditions子方法功能一致,都可以用来初始化离散、连续状态变量和Dwork向量,但是二者也存在区别。Start子方法仅仅在仿真执行开始时初始化一次,而S函数模块放置在使能子系统中时,其InitializeConditions子方法在每次子系统被使能时都会被调用。
4.Output子方法
Output子方法跟Level 1 M S函数的mdlOutputs子方法作用一样,用于计算S函数的输出。下面的代码将Dwork向量值赋给输出端口作为当前采样时刻的输出值。
function Outputs(block)
block.OutputPort(1).Data = block.Dwork(1).Data;
%endfunction
5.Update子方法
Update子方法跟Level 1 M S函数中的mdlUpdate子方法作用相同,用于计算离散状态变量的值。下面代码将当前采样时刻的输入端口值幅值给Dwork向量:
function Update(block)
block.Dwork(1).Data = block.InputPort(1).Data;
%endfunction
6.Derivatives子方法
Derivatives子方法跟Level 1 M S函数中的mdlDerivatives子方法作用相同用于计算并更新连续状态变量的值。下面代码将当前采样时刻的输入端口值赋给连续状态变量:
function Derivatives(block)
block.Derivatives(1).Data = block.InputPort(1).Data;
%endfunction
7.Terminate子方法
S函数工作的首位工作放在Terminate子方法中进行,如存储空间的释放,变量的删除等。Level 2 M S函数不要求必须包含Terminate子方法。
例子
融合2张图像。

两张图片的尺寸是[375×500×3]的uint8类型,即使是Level 2 M S函数也不能处理3维数据矩阵,对多支持二维数据。需要使用M脚本进行预处理,然后再S函数内部实现数据融合的计算。图片的第三维存储信息是每个像素点的RGB信息,若仅取RGB其中一组信息,那么图片就变成灰度图片,同时图片的第三维数据就被取出了从而变成二维矩阵,适合Level 2 M S函数进行处理。模块有两个输入,每个输入的维数是二维数据,375×500的矩阵,数据类型均为uint8.模块没有状态变量和输出端口,故不需要实现S函数的Update,Output子方法。模块在Terminate子方法中实现两个端口输入的矩阵进行融合的代码,并拖过figure展示融合后的图片。
首先在工作空间中将图片的信息读入并取出R维色彩信息以转化为二维矩阵。
m1 = imread('阿布罗狄.jpg');
m1 = m1(:,:,1);
m2 = imread('艾欧里亚.jpg');
m2 = m1(:,:,1);
在模型中可以使用Constant模块将图片转化之后的数据读入,在Constant Value处使用imread函数读取后得到的变量。
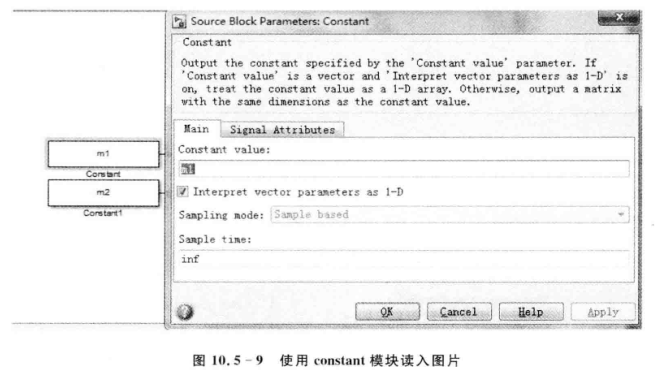
编写名为sfun_image_merge的S函数:
setup(block);%设置模块
%endfunction
% Function: setup ===================================================
% Abstract:
% Set up the S-function block's basic characteristics such as:%设定基础参数
% - Input ports%输入端口
% - Output ports%输出端口
% - Dialog parameters%对话参数
% - Options%选项
%
% Required : Yes
% C MEX counterpart: mdlInitializeSizes
%
function setup(block)
% Register the number of ports.设置输入输出端口数
block.NumInputPorts = 2;
block.NumOutputPorts = 0;
% Set up the port properties to be inherited or dynamic.将端口属性设置为继承或动态。以指示输入和输出端口从模型继承其已编译属性(尺寸,数据类型,复杂度和采样模式)
block.SetPreCompInpPortInfoToDynamic;%设定输入端口属性为动态
% Override the input port properties.覆盖输入端口属性
block.InputPort(1).DatatypeID = 3; % uint8
block.InputPort(1).Complexity = 'Real';
block.InputPort(2).DatatypeID = 3; % uint8
block.InputPort(2).Complexity = 'Real';
% Hard-code certain port properties
block.InputPort(1).Dimensions = [375 500];
block.InputPort(1).DirectFeedthrough = false;
block.InputPort(2).Dimensions = [375 500];
block.InputPort(2).DirectFeedthrough = false;
%Register parameters
block.NumDialogPrms = 0;
% Set up the continuous states.设定具有连续状态变量个数
% block.NumContStates = 1;
% Register the sample times.设定采样时间
% [0 offset] : Continuous sample time连续的采样时间
% [positive_num offset] : Discrete sample time离散的采样时间
%
% [-1, 0] : Inherited sample time继承的采样时间
% [-2, 0] : Variable sample time可变采样时间
block.SampleTimes = [0 0];%设定上面的采样时间,设置为[-1 0]即制定S函数具有继承的采样时间
block.SimStateCompliance = 'DefaultSimState';
% -----------------------------------------------------------------
% Register the methods called during update diagram/compilation.
% -----------------------------------------------------------------
%
% PostPropagationSetup:
% Functionality : Set up the work areas and the state variables. You can
% also register run-time methods here.
% C MEX counterpart: mdlSetWorkWidths
%
% block.RegBlockMethod('PostPropagationSetup', @DoPostPropSetup);
%
% InitializeConditions:
% Functionality : Call to initialize the state and the work
% area values.
% C MEX counterpart: mdlInitializeConditions
%
% block.RegBlockMethod('InitializeConditions', @InitializeConditions);
%
% Outputs:
% Functionality : Call to generate the block outputs during a
% simulation step.
% C MEX counterpart: mdlOutputs
%
% block.RegBlockMethod('Outputs', @Outputs);
%
% Update:
% Functionality : Call to update the discrete states
% during a simulation step.
% C MEX counterpart: mdlUpdate
%
% block.RegBlockMethod('Update', @Update);
%
% Derivatives:
% Functionality : Call to update the derivatives of the
% continuous states during a simulation step.
% C MEX counterpart: mdlDerivatives
%
% block.RegBlockMethod('Derivatives', @Derivatives);
%
% Terminate:
% Functionality : Call at the end of a simulation for cleanup.
% C MEX counterpart: mdlTerminate
%
block.RegBlockMethod('Terminate', @Terminate);
function Terminate(block)
imshow((block.InputPort(1).data + block.InputPort(2).data) / 2);
%endfunction
使用Level 2 M S函数模块,将S函数名sfun_image_merge填入S-Function Name栏,构成如图所示模型。
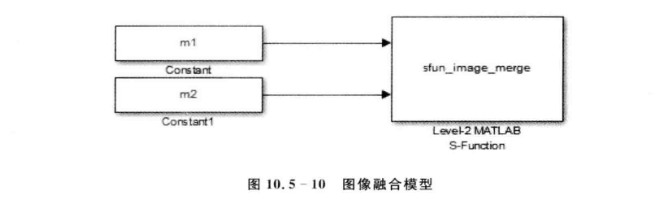
仿真得到图像。
编写自己的Level 2 M S函数时可以使用Simulink提供的模板作为基础,然后进行内容增加或删减。msfun_test.m就是其中一个常用的模板。
明天自己编写一个Level 2 M S函数的模板吧。