在进行电弧模型建模时候,传统的cassie电弧模型的写法都是连续的,但是连续状态的采样率设置上就出现了问题,无法按照自己期望的采样率进行仿真,所以需要对模型进行离散化处理。
转自csdn

建立微分方程只是解决问题的第一步通常需要求出方程的解来说明实际现象,并加以检验。如果能得到即系形式的解固然是便于分析和应用的,但是我们知道,只有线性常系数微分方程,并且自由项是某些特殊类型的函数时,才可以肯定得到这样的解,而绝大多数变系数方程、非线性方程都是所谓“解不出来”的,即使看起来非常简单的方程如$\frac{d y}{d x}=y^{2}+x^{2}$,对于用微分方程解决实际问题来说,数值解法就是一个十分重要的手段。
1. 常微分方程离散化
下面主要讨论一阶常微分方程的初值问题,其一般形式是
\[\left\{\begin{array}{l} {\frac{d y}{d x}=f(x, y) \quad a \leq x \leq b} \\ {y(a)=y_{0}} \end{array}\right.\tag{1}\]在下面讨论中,我们总假定函数$f(x,y)$连续,且关于y满足Lipschitz条件,即存在常数L,使得
\[|f(x, y)-f(x, \bar{y})| \leq L|y-\bar{y}|\]这样,由常微分方程理论知,处置问题(1)的解必定存在唯一。
数值解法
所谓数值解法,就是求问题(1)的解$y(x)$在若干点
$a=x_{0}<x_{1}<x_{2}<\cdots<x_{N}=b$处的近似值$y_n(n=1,2,…,N)$,$y_n(n=1,2,…,N)$称为问题(1)的数值解,$h_n=x_{n+1}-x_n$称为由$x_n$到$x_{n+1}$的步长,今后如无特别说明,我们总取步长为常量h。
建立数值解法,首先要将微分方程离散化,一般采用以下几种方法:
(i)用差商近似导数——缠粉方程初值问题
若用向前差商$\frac{y\left(x_{n+1}\right)-y\left(x_{n}\right)}{h}$代替$y^{\prime}\left(x_{n}\right)$带入(1)中的微分方程,则得
\[\frac{y\left(x_{n+1}\right)-y\left(x_{n}\right)}{h} \approx f\left(x_{n}, y\left(x_{n}\right)\right) \quad(n=0,1, \cdots)\]简化得
\[y\left(x_{n+1}\right) \approx y\left(x_{n}\right)+h f\left(x_{n}, y\left(x_{n}\right)\right)\]如果用$y(x_n)$的近似值$y_n$带入上式右端,所得结果作为$y(x_{n+1})$的近似值,记为$y_{n+1}$,则有
\[y_{n+1}=y_{n}+h f\left(x_{n}, y_{n}\right) \quad(n=0,1, \cdots)\tag{2}\]这样,问题(1)的近似解可通过求解下述问题
\[\left\{\begin{array}{l} {y_{n+1}=y_{n}+h f\left(x_{n}, y_{n}\right) \quad(n=0,1, \cdots)} \\ {y_{0}=y(a)} \end{array}\right.\tag{3}\]按式(3)由初值$y_0$可逐次算出$y_1,y_2…$。式(3)是个离散化的问题,成为差分方程初值问题。
(ii)用数值积分方法
将问题(1)的解表成积分形式,用数值积分方法离散化。例如,对微分方程两端积分,得
\[y\left(x_{n+1}\right)-y\left(x_{n}\right)=\int_{x_{n}}^{x_{n+1}} f(x, y(x)) d x \quad(n=0,1, \cdots)\tag{4}\]右边的积分用矩形公式或梯形公式计算。
(iii)Taylor多项式近似
将函数$y(x)$在$x_n$处展开,取一次Taylor多项式近似,则得
\[y\left(x_{n+1}\right) \approx y\left(x_{n}\right)+h y^{\prime}\left(x_{n}\right)=y\left(x_{n}\right)+h f\left(x_{n}, y\left(x_{n}\right)\right)\]再将$y(x_n)$的近似值$y_n$代入上式右端,所得结果作为$y(x_{n+1})$的近似值$y_{n+1}$,得到离散化的计算公式
\[y_{n+1}=y_{n}+h f\left(x_{n}, y_{n}\right)\]以上三种方法都是将微分方程离散化的常用方法,每一类方法又可导出不同形式的计算公式。其中Taylor展开法,不仅可以得到求数值解的公式,而且容易估计截断误差。
2 欧拉(Euler)方法
2.1 向前Euler公式、向后Euler公式
Euler方法就是用查分方程初值问题(3)的解来近似微分方程初值问题(1)的解,即由公式(3)依次算出$y(x_n)$的近似值$y_n$,($n=1,2,…$)。这组公式求问题(1)的数值解成为向前Euler公式。
如果在微分方程离散化时,用向后差商代替导数,即$y^{\prime}\left(x_{n+1}\right) \approx \frac{y\left(x_{n+1}\right)-y\left(x_{n}\right)}{h}$,则得计算公式
\[\left\{\begin{array}{l} {y_{n+1}=y_{n}+h f\left(x_{n+1}, y_{n+1}\right) \quad(n=0,1, \cdots)} \\ {y_{0}=y(a)} \end{array}\right.\tag{5}\]用这组公式求问题(1)的数值解成为向后Euler公式。
向后Euler法与Euler法形式上相似,但实际计算时却复杂的多。向前Euler公式是显式的,可直接求解。向后Euler公式的右端含有$y_{n+1}$,因此是隐式公式,一般要用迭代法求解,迭代公式通常为
\[\left\{\begin{array}{l} {y_{n+1}^{(0)}=y_{n}+h f\left(x_{n}, y_{n}\right)} \\ {y_{n+1}^{(k+1)}=y_{n}+h f\left(x_{n+1}, y_{n+1}^{(k)}\right) \quad(k=0,1,2, \cdots)} \end{array}\right.\tag{6}\]2.2 Euler方法的误差估计
对于向前Euler公式(3)我们看到,当n = 1,2,……时公式右端的$y_n$都是近似的,所以用它计算的$y_{n+1}$会有累积误差,分析累积误差比较复杂,这里先讨论比较简单的所谓局部截断误差。
假定用(3)式右端的$y_n$没有误差,即$y_n=y(x_n)$,那么由此算出
\[y_{n+1}=y\left(x_{n}\right)+h f\left(x_{n}, y\left(x_{n}\right)\right)\tag{7}\]局部截断误差指的是,按(7)式计算由$x_n$到$x_{n+1}$这一步的计算值$y_{n+1}$与精确值$y(x_{n+1})$之差$y(x_{n+1})-y_{n+1}$。为了估计它,由Taylor展开得到的精确值$y(x_{n+1})$是
\[y\left(x_{n+1}\right)=y\left(x_{n}\right)+h y^{\prime}\left(x_{n}\right)+\frac{h^{2}}{2} y^{\prime \prime}\left(x_{n}\right)+O\left(h^{3}\right)\tag{8}\](7)、(8)两式相减(注意到$\left.y^{\prime}=f(x, y)\right)$)得
\[y\left(x_{n+1}\right)-y_{n+1}=\frac{h^{2}}{2} y^{\prime \prime}\left(x_{n}\right)+O\left(h^{3}\right) \approx O\left(h^{2}\right)\tag{9}\]即局部截断误差是$h^2$阶的,而数值算法的精度定义为:
若一种算法的局部截断误差为$O(h^{p+1})$,则称该算法具有p阶精度。
显然p越大,方法的精度越高。式(9)说明,向前Euler方法是一阶方法,因此它的精度不高。
3 改进的Euler方法
3.1 梯形公式
利用数值积分方法将微分方程离散化时,若用梯形公式计算式(4)中之右端积分,即。
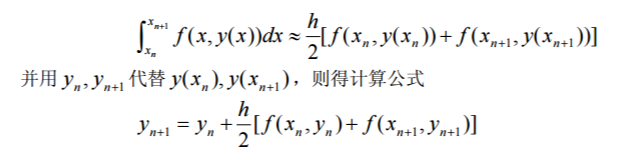
这就是求解初值问题(1)的梯形公式。
直观上容易看出,用梯形公式计算数值积分要比矩形公式好。梯形公式为二阶方法。 梯形公式也是隐式格式,一般需用迭代法求解,迭代公式为
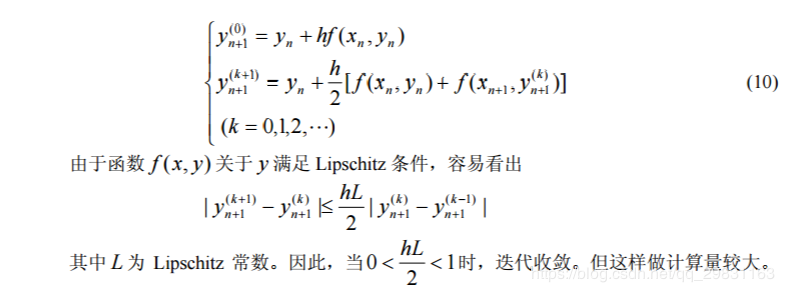
如果实际计算时精度要求不太高,用公式(10)求解时,每步可以只迭代一次,由此导 出一种新的方法—改进 Euler 法。
3.2 改进Euler法
按式(5)计算问题(1)的数值解,如果每步只迭代一次,相当于将Euler公式与梯形公式结合使用:先用Euler公式求$y_n+1$的一个初步近似值$\bar{y}_{n+1}$,称为预测值,然后用梯形公式校正求得近似值$y_n+1$,即
\[\left\{\begin{array}{l} {\bar{y}_{n+1}=y_{n}+h f\left(x_{n}, y_{n}\right)} \\ {y_{n+1}=y_{n}+\frac{h}{2}\left[f\left(x_{n}, y_{n}\right)+f\left(x_{n+1}, \bar{y}_{n+1}\right)\right]} \end{array}\right.\tag{11}\]式(11)称为由Euler公式和梯形公式得到的预测——校正系统,也叫改进Euler法。
为了便于编制程序上机,式(11)常改写成
\[\left\{\begin{array}{l} {y_{p}=y_{n}+h f\left(x_{n}, y_{n}\right)} \\ {y_{q}=y_{n}+h f\left(x_{n}+h, y_{p}\right)} \\ {y_{n+1}=\frac{1}{2}\left(y_{p}+y_{q}\right)} \end{array}\right.\tag{12}\]改进Euler法是二阶方法。
4 龙格——库塔(Runge-Kutta)方法
这部分以后再补,暂时用不上。
https://blog.csdn.net/qq_29831163/article/details/89703598
5 Matlab解法
https://blog.csdn.net/qq_29831163/article/details/89703911
5.1 非刚性常微分方程的解法
Matlab 的工具箱提供了几个解非刚性常微分方程的功能函数,如 ode45,ode23, ode113,其中 ode45 采用四五阶 RK 方法,是解非刚性常微分方程的首选方法,ode23 采用二三阶 RK 方法,ode113 采用的是多步法,效率一般比 ode45 高。 Matlab 的工具箱中没有 Euler 方法的功能函数。
(1)对简单的一阶方程的初值问题
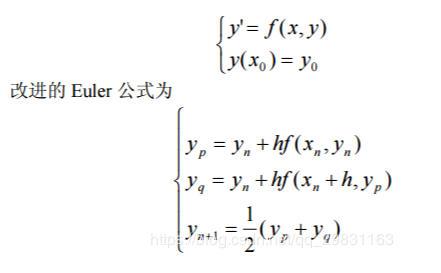
自己编写改进的Euler方法函数eulerpro.m如下:
function [x,y]=eulerpro(fun,x0,xfinal,y0,n);
if nargin<5,n=50;end
h=(xfinal-x0)/n;
x(1)=x0;y(1)=y0;
for i=1:n
x(i+1)=x(i)+h;
y1=y(i)+h*feval(fun,x(i),y(i));
y2=y(i)+h*feval(fun,x(i+1),y1);
y(i+1)=(y1+y2)/2;
end