一个常规的微分方程。
$\frac { d y } { d t } = a y + e ^ { s t }$ $y = y(0) at t = 0$ Look for $y_p = Ye^{st}$
把$\frac { d y } { d t }$比做银行的钱的增长率,$y$就是银行的利息,$e ^ { s t }$代表挣到的钱,是指数形式的,$s$代表souce,源,t代表时间。
带入$y_p = Ye^{st}$,得到$Y = \frac {1}{s-a}$
则 $y(t) = \frac{e^{st}}{s-a} + null solution$
null solution的意思是,输入项没有了,也就是$e^{st} = 0$,求$\frac { d y } { d t } = a y$,得$y = e^{at}$
所以,通解
$y(t) = \frac{e^{st}}{s-a} + Ce^{at} = y_p + y_n\tag{1}$
y_p意思是y_particular,y_n意思是y_null。
将$y = y(0) at t = 0$带入得特解
$y(0) = \frac {1}{s-a} + C$
则$C = y(0) - \frac {1}{s-a}$,带回(1)得,将y(0)单独提出来
$\begin{aligned} y ( t ) &\left. = \frac { e ^ { s t } } { s - a } + \left[ y ( 0 \right) - \frac { 1 } { s - a } \right] e ^ { a t } \ & = \frac { e ^ { s t - e ^ { a t } } } { s a } + y ( 0 ) e ^ { a t } \ & = y_{vp} + y_n \end{aligned}$
y_vp是y_very particular。
特接并不唯一。
这个null solution很好,可以看做是从初始状态开始的一个变化,并包含初始状态信息。
这个特别的解很好,有这样的性质,当t=0时,特解同时=0,这样就得到了通解。
但是有一个例外,当s=a时,分母为0,同时分子也为0,这时,就出现了震荡(Resonance)。这时候需要用到洛必达(L‘ Hopital)法则。
IF s = a,then
$y_{vp}+y_n = t e^{at} + y(0)e^{at}\tag{2}$
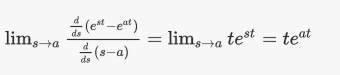
由此得到公式(2)中的特解部分。