基于等效电路的长气隙放电模型
摘要
本文对整个放电模型进行了尝试。该模型建立在等效电网络的基础上,电网络的参数由电磁场和气体放电理论确定。它利用了放电通道可以比作长导体的事实,并对单个导体线采用典型的LCR表示。对于放电的所有阶段,采用相同的电路来模拟变电阻和变电感的阶段变化。对于给定的形状和电极配置,该模型允许我们确定先导电流和回程、相应的电荷、沿先导通道的电位降、注入间隙的功率和能量以及先导传播速度。得到的结果与实验室中产生的长气隙放电的实验结果一致。
1. 引言
了解长气隙T放电的物理机制和表征这种放电的参数对解决各种工程问题是必要的。事实上,高压输电系统面临两种主要类型的电介质应力:由雷击引起的电介质应力和由网络本身运行引起的电介质应力(开关电介质应力)。后者在工程系统尺寸方面具有相当大的经济影响。因此,似乎有必要了解气隙在遇到开关浪涌时的行为。
从实验和理论上获得了关于击穿过程的大量物理知识。事实上,可用的放电模型的作用正在不断增加。大量的工作已经投入到分析不同的参数表征放电,如电流,电荷,传播模式,速度和辐射电磁场。
实际上,有许多数学模型11-61描述了在每个放电阶段(第一电晕开始、流光传播、先导形成、先导传播、最后跳跃、回程)发生的物理过程。然而,所有这些模型都局限于单相,不能组合成一个能够预测给定电压下给定间隙的行为的通用模型。这种困难是由于气体放电中所涉及的现象的复杂性造成的。对各个阶段的描述已在许多出版物中报道[l, 3,4,7]。我们现在只回顾其主要特点。
第一电晕是第一个可见的电离过程,它以丝状通道或流光的形式出现。由于电晕的增长,一个净正电荷迅速地注入到缺口中。在日冕流光的根部,可以观察到一条短而明亮的通道:茎。从后者,形成一段领导信道。在击穿长气隙中最重要的现象只出现在先导传播开始之后。在某些条件下,它之后是一个或多个黑暗时期。根据所施加的电压值,先导传播不一定导致击穿。最后一跳是先导传播的最后阶段,不可避免地会导致间隙短路。当第一束冕流到达飞机时就开始了。
接下来,我们利用LCR线将整个放电现象(先导阶段、末跳阶段和回程阶段)分别由电磁场、气体放电理论和物理定律确定的电感、电容和电阻,建立一个完整的简化模型。对于给定的形状和电极结构,我们确定了先导和回程的电流、相应的电荷、沿先导通道的电位降、注入间隙的功率和能量。然后,对前导传播中涉及的物理现象进行准确的评估,特别是使用能量平衡,以便以更完整的方式确定前导传播速度。所得结果与实验数据进行了比较。
2. 模型基础
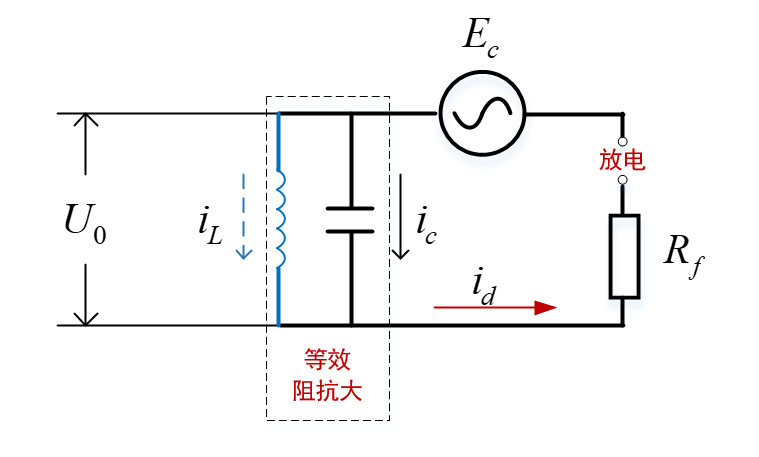
我们已经知道,电路模型在理解等离子体和一些相关过程中发挥了重要作用[5,6,8-10]。在下文中,我们假设放电可以用一个等效的电网表示为如图1所示[6,10],其中$R_0$为平面电极电阻。 在这项工作中,我们将使用的价值100Ω [6,10], $C_0$可以通过球形近似估计,假设两个电极是同心球体,其半径分别为$R_p$和$R_p + D$;D是间隙长度,$R_p$为电极半径,考虑其等于球形电容的一半
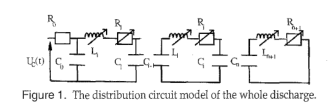
当先导传播时,激发的电位波和电流为
\[L _ { i } \frac { d i _ { i } ( t ) } { d t } = V _ { i - 1 } ( t ) - V _ { i } ( t ) - R _ { i } \dot { \imath } _ { i } ( t ) \tag{2}\] \[i _ { i } ( t ) = C _ { i } ( x ) \frac { d V _ { i } ( t ) } { d t } \tag{3}\]另一方面,我们有
\[i _ { i - 1 } ( t ) - i _ { i } ( t ) = C _ { i - 1 } ( x ) \frac { d V _ { i - 1 } ( t ) } { d t } \tag{4}\]对于建模,我们使用“状态表示”。这包括将一阶微分方程组中的电路方程写成如下形式
\[\frac { d X ( t ) } { d t } = A X ( t ) + B U ( t ) \tag{5}\] \[Y ( t ) = C X ( t ) + D U ( t ) \tag{6}\]其中A、B、C、D分别为系统动力学、控制、观测和直接传输的状态矩阵。U(t)和Y (t)分别为输入矩阵和输出矩阵。
一旦状态向量X被确定,状态矩阵(A, B, C, D)将被计算知道拓扑和电路参数的值。
将式(2)、式(3)代入式(4)即可得到电压。那么,主导电流将是
\[i ( t ) = \frac { V _ { 0 } ( t ) - U ( t ) } { R _ { 0 } } \tag{7}\]$V_0(t)$和$U_c(t)$分别为$C_0$电容电压和施加到间隙的电压。注入缝隙的空间电荷等于基本电荷之和
\[Q ( t ) = \sum _ { 1 } ^ { n } q _ { i } = \sum _ { 0 } ^ { t } C _ { i } V _ { i } ( t ) \tag{8}\]$V_i(t)$为$C_i$电容电压,n为前导步数。
从瞬时电压Uj和高压电流I的数字样本中,通过过度计算得到注入间隙的功率Pj和能量Wj
\[P _ { j } = U _ { j } I _ { j } \tag{9}\] \[W _ { j } = \sum _ { 0 } ^ { i } U _ { j } I _ { j } d t \tag{10}\]其中dt是所选数字样本之间的间隔,等于计算中的$10^{-6}s$。
总动能Wj的一部分转移到先导通道,使先导通道可以延长dlj的距离。注入通道的质量等于气体密度$\rho$与体积增量$\pi r _ { j } ^ { 2 } d l _ { j } $的乘积。
称为$\beta$,总能量的分数部分Wj用于先导传播,我们可以写出每个位移的先导$ d l _ { j } $
\[\frac { 1 } { 2 } \rho \pi r _ { j } ^ { 2 } d l _ { j } \nu _ { j } ^ { 2 } ( t ) = \beta d W _ { j } ( t ) \tag{11}\]$0 < \beta \leq 1$,其中$r_j$和$v_j (t)$分别为导叶尖端半径和速度。
在高温下,所有的气体都被认为是完美的。由于先导是一个高电离等离子体(t3 1000k)[1,11],因此可以应用完美的气体定律。因此
$p V = \frac { m } { M } R T\tag{12}$
其中,V, m, R, T, m分别是压力,体积,通道质量,理想气体常数,温度和通道的摩尔质量。因为密度p = m/V,它变成
$\rho = \frac { M p } { R T } \tag{13}$
leader处于非爆炸阶段,leader的压力可以认为是常数[4,11],近似等于大气压力[1]。因此
$\rho = \frac { k } { T R } \tag{14}$
$\rho$的单位是$kg/m^3$, T的单位是k。在这种情况下,R是温度相关的[12],k = Mp。
由于$dl_j = v_j (t)dt$,并且假设导叶尖端有半径$T_0$和温度$T_0$,我们将有
\[\nu _ { j } ( t ) = [ \frac { 2 \beta T _ { 0 } R d W _ { j } ( t ) } { k \pi r _ { 0 } ^ { 2 } d t } ] ^ { 1 / 3 } \tag{15}\] \[\nu _ { j } ( t ) = [ \frac { 2 \beta T _ { 0 } R } { k \pi r _ { 0 } ^ { 2 } } P _ { j } ( t ) ] ^ { 1 / 3 } \tag{16}\]总能量$\beta$转化为动能的那部分已经在别处估计过了[12]。我们发现$\rho = 0.1$。
在每一次的时候都可以计算注入间隙的能量(或功率),考虑到具体情况在电压和间隙几何等条件下,将有可能计算出前导子的传播速度。
3. 脉冲电压计算
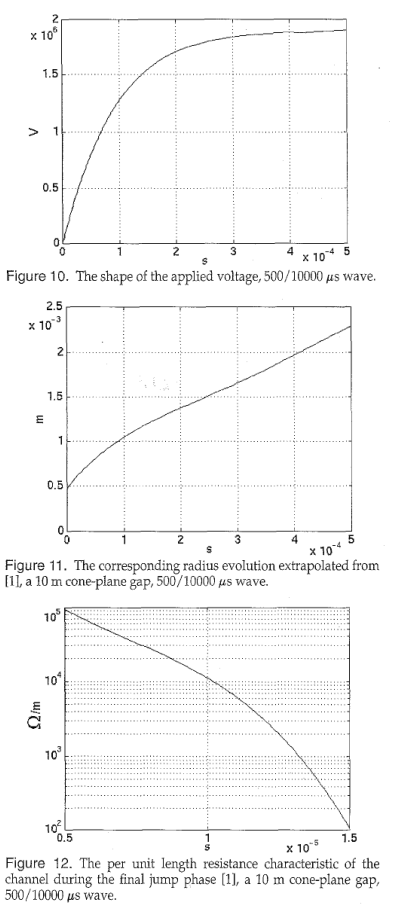
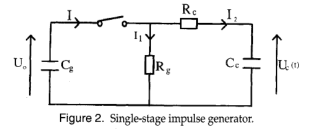
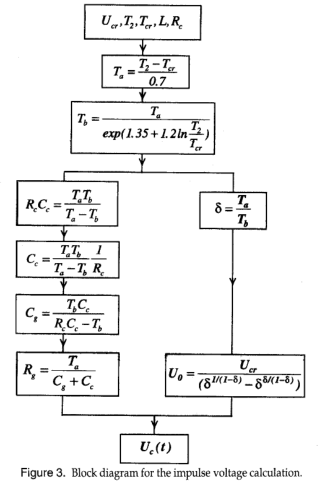
我们已经知道,放电的电流和电荷(先导和回程)取决于在电极间隙处施加的电压。在下面,我们考虑一个类似于文献[4,11]中使用的脉冲电压,以便将我们的结果与这些作者获得的结果进行比较。这种电压的形式是一个双指数脉冲。Marx发生器用于产生这种双指数脉冲,即在不同峰值电压下的正开关脉冲。双指数电压的表达式可以用单级脉冲发生器电路得到。它由一个电容$C_g$组成,它被充电到所需的电压,然后通过一个电路放电,电路的常数可以调整,从而得到所需形状的脉冲电压。单级发电机的基本电路如图2所示。元件$R_g$和$C_g$控制前面,$R_g$和$C_g$,尾部的冲击电压。通过对电路的分析(如图2所示),我们可以得到输出电压$U_c(t)$的表达式。
\[U _ { c } ( t ) = \frac { U _ { 0 } } { R _ { e } C _ { c } } \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } [ \operatorname { exp } ( - \frac { t } { T _ { a } } ) - \operatorname { exp } ( - \frac { t } { T _ { b } } ) ] \tag{17}\]其中$T_a$,$T_b$,$T_2$, $U_0$分别为上升时间,下降时间,到1 / 2的时间和振幅因子。
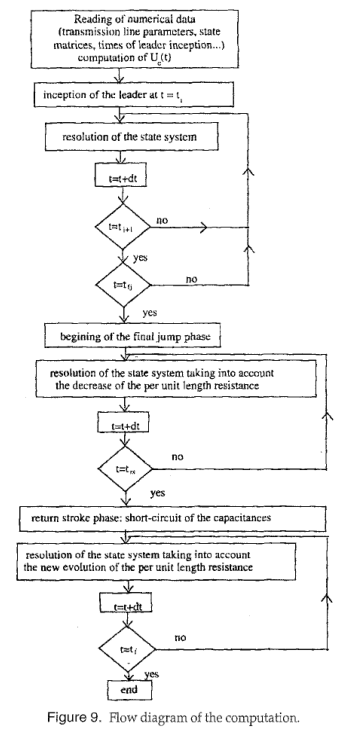
为了确定$U_c (t)$,我们使用图3中给出的框图。图中所示的关系已在以前的著作中阐明。由此可知,放电的时空参数(电流,电荷,…)需要了解$L_i$、$C_i$和$R_i$元素(参见图1)。
4. 等效电路参数
4.1 电阻
在先导传播过程中,其通道充当电阻电极,其特性由欧姆加热和气体动态膨胀控制[1,4]。假设通道为圆柱形,单位长度的电阻将由
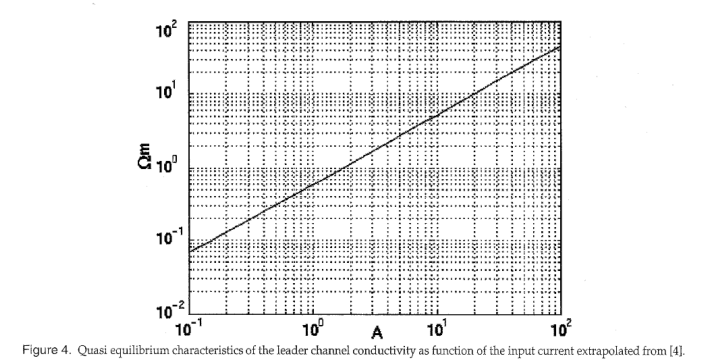
\[\lambda = \frac { 1 } { \sigma \pi a ^ { 2 } ( t ) } \tag{18}\]$\rho$和$a(t)$分别为导星电导率和通道半径。从实验数据推导出导频通道半径$a(t)$的演化过程。然而,领导者的电导率是通过图4得到的,图中特征$\rho = f(I)$给出了电导率作为输入电流的函数,由Les RenardiPres组[4]绘制。
最后的跳跃代表了先导条件从非LTE(局部热力学平衡)特性到火花通道LTE特性的转变。这位领导人似乎在更短的时间内改变了内部条件。在这里,它将对应最后一个单元(图1)和较低的单位长度电阻的领导者。最后跳跃时单位长度阻力的变化将由实验数据[1]给出。
关于返回冲程阶段,我们知道[l]在火花中,等离子体处于LTE状态:气体分子完全游离,通过通道的温度是均匀的。这个阶段对应于在先导传播期间注入间隙的电荷的中和。通道半径由相等的、相互抵消的磁力和动能维持。
高电离气体的电导率为$\rho = 1.5 x 10^{-5}T^{3/2} ( \Omega^{-1} cm^{-1}) $[5]。根据Gallimberti [1],在回程中,长气隙通道内的温度为 20000 K。
4.2 电导
注意,在先导阶段,电感是可以忽略的。因此,计算将执行的回程情况。
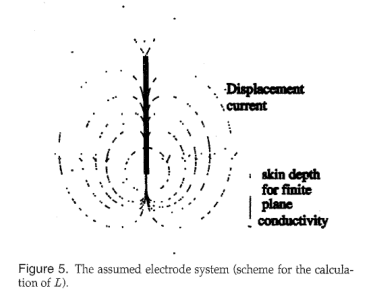
为了确定通道的电感,使用图5所示的简化方法[5]。结束效果被忽略。通道的电感是两个电感之和,即存储在通道L1中的电磁能量产生的电感(内电感)和辐射产生的电感通过通道的电流的电磁场L2。
4.2.1 能量储存在通道中
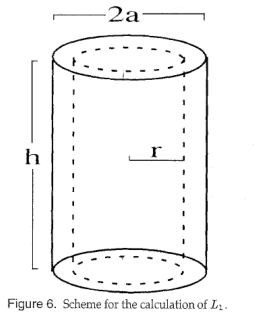
考虑一个高度为h的通道段,如图6所示。我们称I为流过这段的电流。距离$r \leq a$处的磁场相对于通道轴为
\[B ( r ) = \frac { \mu _ { 0 } } { 2 \pi r } \frac { I \pi r ^ { 2 } } { \pi a ^ { 2 } } = \frac { \mu _ { 0 } r } { 2 \pi a ^ { 2 } } I \tag{19}\]所储存的电磁能的密度为
\[\delta \omega ( r ) = \frac { 1 } { 2 \mu _ { 0 } } B ^ { 2 } ( r ) \tag{20}\]或者
\[\delta \omega ( r ) = \frac { \mu _ { 0 } } { 8 \pi ^ { 2 } } I ^ { 2 } \frac { r ^ { 2 } } { a ^ { 4 } } \tag{21}\]假设恒流I,段通道中存储的总电磁能量为
\[W = 2 \pi h \int _ { 0 } ^ { a } \delta \omega ( r ) r d r \tag{22}\]由于
\[W = \frac { \mu _ { 0 } } { 16 \pi } I ^ { 2 } h \tag{23}\]另一方面,这种能量也可以表示为
\[W = \frac { 1 } { 2 } L _ { 1 } I ^ { 2 } \tag{24}\]由式(23)和式(24)可以推导出L1
\[L _ { 1 } = \frac { I } { 4 } \frac { \mu _ { 0 } } { 2 \pi } h \tag{25}\]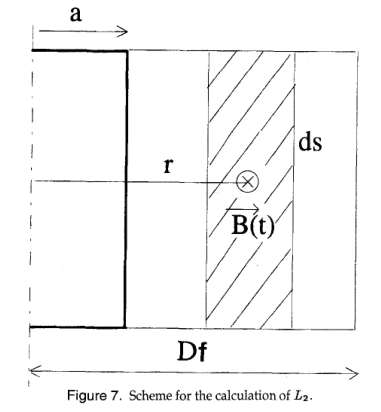
4.2.2 先导通道内的电流
设$D_f$是距离导线的距离,在这一点上电场被认为是零。考虑图7中所示的通道前一段的纵向部分。距离$r (a < r < D_f)$处的磁场定义为
\[B ( r ) = \frac { \mu _ { 0 } I } { 2 \pi r } \tag{26}\]则根据(20),所储存的电磁能的密度为
\[\delta \omega ( r ) = \frac { 1 } { 2 \mu _ { 0 } } \frac { \mu _ { 0 } ^ { 2 } I ^ { 2 } } { 4 \pi ^ { 2 } r ^ { 2 } } = \frac { \mu _ { 0 } I ^ { 2 } } { 8 \pi ^ { 2 } r ^ { 2 } } \tag{27}\]考虑$I$为常数,总存储电磁能为式(22)
\[W = \frac { 2 \pi h \mu _ { 0 } I ^ { 2 } } { 8 \pi ^ { 2 } } \int _ { a } ^ { D f } \frac { d r } { r } = \frac { h \mu _ { 0 } I ^ { 2 } } { 4 \pi } \operatorname { ln } [ \frac { D f } { a } ] \tag{28}\]另一方面,这种能量可以表示为
\[W = \frac { 1 } { 2 } L _ { 2 } I ^ { 2 } \tag{29}\]因此,由式(28)和式(29)
\[L _ { 2 } = \frac { \mu _ { 0 } h } { 2 \pi } \operatorname { ln } [ \frac { D f } { a } ] \tag{30}\]根据(25)和(30),整个系统的电感为
\[L = \frac { \mu _ { 0 } h } { 2 \pi } [ \frac { 1 } { 4 } + \operatorname { ln } ( \frac { D f } { a } ) ] \tag{30}\]根据(25)和(30),整个系统的电感为
\[L = \frac { \mu _ { 0 } h } { 2 \pi } [ \frac { 1 } { 4 } + \operatorname { ln } ( \frac { D f } { a } ) ] \tag{31}\]所以,通道的单位长度电感$L_u(H/m)$是
\[L _ { u } = \frac { \mu _ { 0 } } { 2 \pi } [ 0.25 + \operatorname { ln } ( \frac { D f } { a } ) ] \tag{32}\]注意,对于瞬态字段,Df应该保持较大。分数误差的数量级为l/Zn(D/a)[5]。这是非常小的,因为D f » a。这里提出的工作是关于在实验室中产生的长气隙中的排放。我们取Df = 100 m进行计算。
4.3 电容
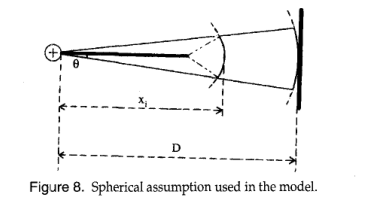
电容Ci是通过一个简单的模型[6,10]得到的,即球形近似。该模型将先导体表示为等离子体通道,其周围包裹着由上述流线引起的电荷。该模型包括假定出料头和面为两个同心圆,由立体角$\Gamma$定义。这两个球体之间的距离随放电的传播而变化(图8)。
考虑到立体角$\Gamma = 2 \pi (1 - cos \theta)< 4 \pi$,电容表达式为
\[C _ { i } = \Gamma \varepsilon _ { o } \frac { D x _ { i } } { D - x _ { i } } = \frac { 4 \pi \varepsilon _ { o } } { \alpha } \frac { D x _ { i } } { D - x _ { i } } \tag{33}\]其中
\[\alpha = \frac { 4 \pi } { \Gamma } \tag{34}\]结果表明,模拟结果与实验结果一致的$\alpha$值为$\alpha = 30$[6,10]
然而,有必要知道施加的电压U(t),放电步长$x_i$和它们的数量,在最后跳跃。
为了验证我们的模型,让我们考虑两个由Les Renardieres [4]和P. Domens [1]进行的实验数据的例子,我们知道施加电压的形状、电极的几何形状和相应的电流(或电荷)。从每一种情况对应的条纹照片可以推导出步长$x_i$。