Simulink基于level2 的s-function函数编写

在用模块搭建时会遇到意想不到的问题，比如解微分方程模块，一旦出现分母为0情况就会报错，而自己编写S-Function就可以提前将为0的分母替换为极小值，既不会报错又基本不会影响计算结果。level2的函数可以配置多输入多输出。同时，MEX的S-Function可以实现更多的回调函数。

1. S-Function Bulder

S-Function Bulder可以简化S函数构建流程，但是不能生成多余1个的输入与输出，对于我来说不适用。

2. 一个基本的C MEX S-Function范例

一个timestwo范例，2倍。

timestwo S-Function包含的回调函数如下图。

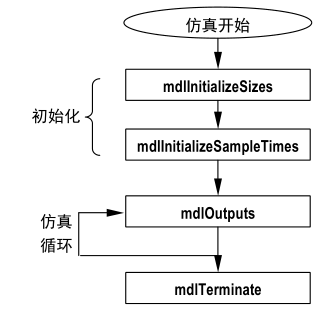
timestwo.c 的内容如下：

#define S_FUNCTION_NAME timestwo
#define S_FUNCTION_LEVEL 2
#include “simstruc.h”
static void mdlInitializeSizes ( SimStruct *S )
{
	ssSetNumSFcnParams( S， 0 )；
	if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount (S)) {
		return； /* Parameter mismatch will be reported by Simulink */
	}
	if ( !ssSetNumInputPorts( S，1 )) return；
	ssSetInputPortWidth (S，0，DYNAMICALLY_SIZED )；
	ssSetInputPortDirectFeedThrough (S，0，1)；
	if ( !ssSetNumOutputPorts (S，1)) return；
	ssSetOutputPortWidth ( S，0，DYNAMICALLY_SIZED )；
	ssSetNumSampleTimes ( S，1)；
	/* Take care when specifying exception free code - see sfuntmpl.doc */
	ssSetOptions ( S，SS_OPTION_EXCEPTION_FREE_CODE )；
}
	static void mdlInitializeSampleTimes ( SimStruct *S )
{
	ssSetSampleTime (S，0，INHERITED_SAMPLE_TIME )；
	ssSetOffsetTime ( S，0，0.0 )；
}
	static void mdlOutputs(SimStruct *S, int_T tid)
{
	int_T I；
	InputRealPtrsType uPtrs = ssGetInputPortRealSignalPtrs ( S，0 )；
	real_T *y = ssGetOutputPortRealSignal (S，0 )；
	int_T width = ssGetOutputPortWidth ( S，0 )；
	for ( i=0；i<width；i++ ) {
		*y++ = 2.0 *( *uPtrs[ I ] )；
	}
}
static void mdlTerminate (SimStruct *S) { }

#ifdef MATLAB_MEX_FILE /* Is this file being compiled as a MEX-file? */
#include “simulink.c” /* MEX-file interface mechanism */
#else
#include “cg_sfun.h” /* Code generation registration function */
#endif

该范例包括三个部分：

• 定义与包含
• 回调函数的实现
• Simulink接口

2.1 定义与包含

该范例以一下的定义开头：

#define S_FUNCTION_NAME timestwo
#define S_FUNCTION_LEVEL 2
#include "simstruc.h"

第一条指定S-function的名字(timestwo)，第二条指定了该S-function是按照level2的格式进行编写的。然后包含的以头文件“simstruc.h”。

2.2 回调函数的实现

mdlInitializeSizes

Simulink调用mdlInitializeSizes来获取输入端口和输出端口的数量、端口宽度等信息。

• 无参数——S-function对话框的S-function parameters区必须为空。如果在此处输入了任何参数，Simulink将报告参数不匹配信息。
• 一个输入端口与一个输出端口——输入和输出端口的宽度是动态的。
• 一个采样时间——timestwo范例在程序mdlInitializeSampleTimes中指定了采样时间的实际值。
• 代码无异常检测——制定exception-free代码可以提高S-function的执行速度。在指定该选项时必须特别小心。

mdlInitializeSampleTimes

调用mdlInitialzeSampleTimes来设置S-function的采样时间。

mdlOutputs

在每个采样时间步长内，Simulink调用mdlOutpus来计算块的输出。

timestwo的mdlOutputs函数使用了SimStruct的一个宏：

InputRealPtrsType uPtrs = ssGetInputPortRealSignalPtrs（S,0）;

来获取输入信号。该宏返回一个向量的指针，必须使用 *uPtrs[i]来访问它。

timestwo的mdlOutputs函数使用了SimStruct的一个宏：

real_T   *y = ssGetOutputPortRealSignal(S,0);

来访问输出信号。该宏返回一个包含了输出向量的指针。

S-function使用int_T width = ssGetOutputPortWidth(S,0)来获取块传递的信号宽度。最后，S-function采用循环通过输入来计算输出。

mdlTerminate

执行仿真结束时的任务。这是一个托管S-function程序。但是，timestwo S-function不需要执行任何终止动作，所以该程序是空的。

Building Timestwo范例

要将此S-function结合到Simulink中，在MATLAB命令行输入下面的命令：

mex timestwo.c

mex命令将timestwo.c编译和链接以生成一个可动态下载的可执行文件，供Simulink使用。

最后的可执行文件是一个MEX S-funciton文件，其中，MEX 代表了MATLAB EXecutable（可执行文件）。MEX文件的扩展名根据不同的平台而有所不同，例如，在Microsoft Windows中，MEX文件的扩展名为.dll。

function msfuntmpl(block) %MSFUNTMPL A Template for a MATLAB S-Function % The MATLAB S-function is written as a MATLAB function with the % same name as the S-function. Replace ‘msfuntmpl’ with the name % of your S-function.

% Copyright 2003-2018 The MathWorks, Inc.

% % The setup method is used to setup the basic attributes of the % S-function such as ports, parameters, etc. Do not add any other % calls to the main body of the function.
％设置方法用于设置S功能的基本属性，例如端口，参数等。请勿在功能主体上添加其他任何调用。 %

setup(block);%设置模块

%endfunction

% Function: setup =================================================== % Abstract: % Set up the S-function block’s basic characteristics such as:%设定基础参数 % - Input ports%输入端口 % - Output ports%输出端口 % - Dialog parameters%对话参数 % - Options%选项 % % Required : Yes % C MEX counterpart: mdlInitializeSizes % function setup(block)

% Register the number of ports.设置输入输出端口数 block.NumInputPorts = 1; block.NumOutputPorts = 1;

% Set up the port properties to be inherited or dynamic.将端口属性设置为继承或动态。以指示输入和输出端口从模型继承其已编译属性（尺寸，数据类型，复杂度和采样模式） block.SetPreCompInpPortInfoToDynamic;%设定输入端口属性为动态 block.SetPreCompOutPortInfoToDynamic;%设定输出端口属性为动态

% Override the input port properties.覆盖输入端口属性 block.InputPort(1).DatatypeID = 0; % double block.InputPort(1).Complexity = ‘Real’;

% Override the output port properties.覆盖输出端口属性 block.OutputPort(1).DatatypeID = 0; % double block.OutputPort(1).Complexity = ‘Real’;

% Register the parameters.初始化对话框参数 block.NumDialogPrms = 3;%初始化三个S函数对话框参数 block.DialogPrmsTunable = {‘Tunable’,’Nontunable’,’SimOnlyTunable’};%参数是否可变

% Set up the continuous states.设定具有连续状态变量个数 block.NumContStates = 1;

% Register the sample times.设定采样时间 % [0 offset] : Continuous sample time连续的采样时间 % [positive_num offset] : Discrete sample time离散的采样时间 % % [-1, 0] : Inherited sample time继承的采样时间 % [-2, 0] : Variable sample time可变采样时间 block.SampleTimes = [0 0];%设定上面的采样时间，设置为[-1 0]即制定S函数具有继承的采样时间

% —————————————————————– % Options选相 % —————————————————————– % Specify if Accelerator should use TLC or call back to the % MATLAB file %指定Accelerator是否使用TLC还是调回MATLAB文件 block.SetAccelRunOnTLC(false);%否，不使用

% Specify the block’s operating point compliance. The block operating % point is used during the containing model’s operating point save/restore) %指定块的工作点符合性。 在包含模型的工作点保存/恢复期间使用块工作点） % The allowed values are:允许的值有 % ‘Default’ : Same the block’s operating point as of a built-in block与内置块相同的块的工作点 % ‘UseEmpty’: No data to save/restore in the block operating point没有数据要在块操作点中保存/恢复 % ‘Custom’ : Has custom methods for operating point save/restore具有用于保存/还原工作点的自定义方法 % (see GetOperatingPoint/SetOperatingPoint below) % ‘Disallow’: Error out when saving or restoring the block operating point.保存或恢复块操作点时出错。 block.OperatingPointCompliance = ‘Default’;%默认

% —————————————————————– % The MATLAB S-function uses an internal registry for all % block methods. You should register all relevant methods % (optional and required) as illustrated below. You may choose % any suitable name for the methods and implement these methods % as local functions within the same file. %MATLAB S函数将内部注册表用于所有块方法。 您应该注册所有相关方法（可选和必需），如下所示。 您可以为这些方法选择任何合适的名称，并将这些方法实现为同一文件中的本地函数。 % —————————————————————–

% —————————————————————– % Register the methods called during update diagram/compilation.注册在更新图/编译期间调用的方法。 % —————————————————————–

% % CheckParameters:检查参数 % Functionality : Called in order to allow validation of the % block dialog parameters. You are % responsible for calling this method % explicitly at the start of the setup method. % 功能：调用以允许验证块对话框参数。 您有责任在setup方法开始时显式调用此方法。 % C MEX counterpart: mdlCheckParameters % block.RegBlockMethod(‘CheckParameters’, @CheckPrms);

% % SetInputPortSamplingMode: % Functionality : Check and set input and output port % attributes and specify whether the port is operating % in sample-based or frame-based mode % C MEX counterpart: mdlSetInputPortFrameData. % (The DSP System Toolbox is required to set a port as frame-based) % block.RegBlockMethod(‘SetInputPortSamplingMode’, @SetInpPortFrameData);

% % SetInputPortDimensions: % Functionality : Check and set the input and optionally the output % port dimensions. % C MEX counterpart: mdlSetInputPortDimensionInfo % block.RegBlockMethod(‘SetInputPortDimensions’, @SetInpPortDims);

% % SetOutputPortDimensions: % Functionality : Check and set the output and optionally the input % port dimensions. % C MEX counterpart: mdlSetOutputPortDimensionInfo % block.RegBlockMethod(‘SetOutputPortDimensions’, @SetOutPortDims);

% % SetInputPortDatatype: % Functionality : Check and set the input and optionally the output % port datatypes. % C MEX counterpart: mdlSetInputPortDataType % block.RegBlockMethod(‘SetInputPortDataType’, @SetInpPortDataType);

% % SetOutputPortDatatype: % Functionality : Check and set the output and optionally the input % port datatypes. % C MEX counterpart: mdlSetOutputPortDataType % block.RegBlockMethod(‘SetOutputPortDataType’, @SetOutPortDataType);

% % SetInputPortComplexSignal: % Functionality : Check and set the input and optionally the output % port complexity attributes. % C MEX counterpart: mdlSetInputPortComplexSignal % block.RegBlockMethod(‘SetInputPortComplexSignal’, @SetInpPortComplexSig);

% % SetOutputPortComplexSignal: % Functionality : Check and set the output and optionally the input % port complexity attributes. % C MEX counterpart: mdlSetOutputPortComplexSignal % block.RegBlockMethod(‘SetOutputPortComplexSignal’, @SetOutPortComplexSig);

% % PostPropagationSetup: % Functionality : Set up the work areas and the state variables. You can % also register run-time methods here. % C MEX counterpart: mdlSetWorkWidths % block.RegBlockMethod(‘PostPropagationSetup’, @DoPostPropSetup);

% —————————————————————– % Register methods called at run-time % —————————————————————–

% % ProcessParameters: % Functionality : Call to allow an update of run-time parameters. % C MEX counterpart: mdlProcessParameters %
block.RegBlockMethod(‘ProcessParameters’, @ProcessPrms);

% % InitializeConditions: % Functionality : Call to initialize the state and the work % area values. % C MEX counterpart: mdlInitializeConditions % block.RegBlockMethod(‘InitializeConditions’, @InitializeConditions);

% % Start: % Functionality : Call to initialize the state and the work % area values. % C MEX counterpart: mdlStart % block.RegBlockMethod(‘Start’, @Start);

% % Outputs: % Functionality : Call to generate the block outputs during a % simulation step. % C MEX counterpart: mdlOutputs % block.RegBlockMethod(‘Outputs’, @Outputs);

% % Update: % Functionality : Call to update the discrete states % during a simulation step. % C MEX counterpart: mdlUpdate % block.RegBlockMethod(‘Update’, @Update);

% % Derivatives: % Functionality : Call to update the derivatives of the % continuous states during a simulation step. % C MEX counterpart: mdlDerivatives % block.RegBlockMethod(‘Derivatives’, @Derivatives);

% % Projection: % Functionality : Call to update the projections during a % simulation step. % C MEX counterpart: mdlProjections % block.RegBlockMethod(‘Projection’, @Projection);

% % SimStatusChange: % Functionality : Call when simulation enters pause mode % or leaves pause mode. % C MEX counterpart: mdlSimStatusChange % block.RegBlockMethod(‘SimStatusChange’, @SimStatusChange);

% % Terminate: % Functionality : Call at the end of a simulation for cleanup. % C MEX counterpart: mdlTerminate % block.RegBlockMethod(‘Terminate’, @Terminate);

% % GetOperatingPoint: % Functionality : Return the operating point of the block. % C MEX counterpart: mdlGetOperatingPoint % block.RegBlockMethod(‘GetOperatingPoint’, @GetOperatingPoint);

% % SetOperatingPoint: % Functionality : Set the operating point data of the block using % from the given value. % C MEX counterpart: mdlSetOperatingPoint % block.RegBlockMethod(‘SetOperatingPoint’, @SetOperatingPoint);

% —————————————————————– % Register the methods called during code generation. % —————————————————————–

% % WriteRTW: % Functionality : Write specific information to model.rtw file. % C MEX counterpart: mdlRTW % block.RegBlockMethod(‘WriteRTW’, @WriteRTW); %endfunction

% ——————————————————————- % The local functions below are provided to illustrate how you may implement % the various block methods listed above. %提供下面的局部功能是为了说明如何实现上面列出的各种块方法。 % ——————————————————————-

function CheckPrms(block)

a = block.DialogPrm(1).Data; if ~isa(a, ‘double’) me = MSLException(block.BlockHandle, message(‘Simulink:blocks:invalidParameter’)); throw(me); end

%endfunction

function ProcessPrms(block)

block.AutoUpdateRuntimePrms;

%endfunction

function SetInpPortFrameData(block, idx, fd)

block.InputPort(idx).SamplingMode = fd; block.OutputPort(1).SamplingMode = fd;

%endfunction

function SetInpPortDims(block, idx, di)

block.InputPort(idx).Dimensions = di; block.OutputPort(1).Dimensions = di;

%endfunction

function SetOutPortDims(block, idx, di)

block.OutputPort(idx).Dimensions = di; block.InputPort(1).Dimensions = di;

%endfunction

function SetInpPortDataType(block, idx, dt)

block.InputPort(idx).DataTypeID = dt; block.OutputPort(1).DataTypeID = dt;

%endfunction

function SetOutPortDataType(block, idx, dt)

block.OutputPort(idx).DataTypeID = dt; block.InputPort(1).DataTypeID = dt;

%endfunction

function SetInpPortComplexSig(block, idx, c)

block.InputPort(idx).Complexity = c; block.OutputPort(1).Complexity = c;

%endfunction

function SetOutPortComplexSig(block, idx, c)

block.OutputPort(idx).Complexity = c; block.InputPort(1).Complexity = c;

%endfunction

function DoPostPropSetup(block) block.NumDworks = 2;

block.Dwork(1).Name = ‘x1’; block.Dwork(1).Dimensions = 1; block.Dwork(1).DatatypeID = 0; % double block.Dwork(1).Complexity = ‘Real’; % real block.Dwork(1).UsedAsDiscState = true;

block.Dwork(2).Name = ‘numPause’; block.Dwork(2).Dimensions = 1; block.Dwork(2).DatatypeID = 7; % uint32 block.Dwork(2).Complexity = ‘Real’; % real block.Dwork(2).UsedAsDiscState = true;

% Register all tunable parameters as runtime parameters. block.AutoRegRuntimePrms;

%endfunction

function InitializeConditions(block)

block.ContStates.Data = 1;

%endfunction

function Start(block)

block.Dwork(1).Data = 0; block.Dwork(2).Data = uint32(1);

%endfunction

function WriteRTW(block)

block.WriteRTWParam(‘matrix’, ‘M’, [1 2; 3 4]); block.WriteRTWParam(‘string’, ‘Mode’, ‘Auto’);

%endfunction

function Outputs(block)

block.OutputPort(1).Data = block.Dwork(1).Data + block.InputPort(1).Data;

%endfunction

function Update(block)

block.Dwork(1).Data = block.InputPort(1).Data;

%endfunction

function Derivatives(block)

block.Derivatives.Data = 2*block.ContStates.Data;

%endfunction

function Projection(block)

states = block.ContStates.Data; block.ContStates.Data = states+eps;

%endfunction

function SimStatusChange(block, s)

block.Dwork(2).Data = block.Dwork(2).Data+1;

if s == 0 disp(‘Pause in simulation.’); elseif s == 1 disp(‘Resume simulation.’); end

%endfunction

function Terminate(block)

disp([‘Terminating the block with handle ‘ num2str(block.BlockHandle) ‘.’]);

%endfunction

function operPointData = GetOperatingPoint(block) % package the Dwork data as the entire operating point of this block operPointData = block.Dwork(1).Data;

%endfunction

function SetOperatingPoint(block, operPointData) % the operating point of this block is the Dwork data (this method % typically performs the inverse actions of the method GetOperatingPoint) block.Dwork(1).Data = operPointData;

%endfunction

若电导不取绝对值，则计算出的电弧电压是13kV，目前设置一个tau=80000us。

可是这样总是没有零休特性的，如何得到零休特性呢？

若电导取绝对值，计算出的电弧电压为6kV。

计算出的tau仍然没什么变化，都是3e7，这应该是有些问题的，不应该这么大，如果这是秒的话，这也太大了些。怎么也不应该超过20ms的，即20000us。

若换成6kV，tau=80000us，试试PSCAD仿真情况。

e=6kV，tau=40000us

电弧电压变得很大，并没有有效提供设定参数的电压。

e=6kV，tau=20000us

是不是可以认为，同样有燃弧，但燃弧时间特别短？

可以明显可以看出，在+4~-4kV中，电流几乎都为零，这样的特征如何模拟呢？还是说计算出的电弧电压并不正确，回去找找错误。

目前的接地点电流计算公式是：

I_d = I_0_front - I_0_back;%计算接地点电流 U_Arc = U_F - R_d .* I_d;

验算下这样的计算方式是否正确，用仿真验证一下。

I_front - I_back = Id

这样便不需要管故障电流的流向问题。

可是这样发现故障电流电弧电压的相序差180°，这是因为测量的零序电压相序接错了的问题吗？

现在按照上面的方法，测到的故障线路的电压和电流是反相位的。

那么，一定有一个是反的，要么是测量到的故障相电压相位反了，要么是电流相位反了，需要验证一下。

验证确实是相位反了，估测电压相位不会错，那么只能是电流的相位反了。将电流相位反向，得到如图曲线。

测量电弧电压和电流的曲线如图

可是放大后会变成如图所示样子，电压波形有些不对。

这样的电压波形应该如何用数学进行描述呢？

是不是不应该出现一个电压反向啊，是不是由于电阻测定的不准确导致的，该处应该是一个平台才对呢？

进行了修正后的曲线。

修正后的$e_0$计算得到曲线

基本上可以设定为3kV，这是合理的，那么如何求得$\tau$呢？

可以利用近似的公式求得$\tau$

但是，这样的“经典电弧模型+可变电阻”的模型有缺陷，最低的电阻即可变电阻阻值，这样在电弧稳定燃烧时的电阻表示不正确。同时由于理想电弧模型的零休时间较长，会有比较长的时间里接地故障电阻较大，这会增大接地平均电阻，导致每条线路的电压以及零流有较大偏差。

目前想到的改进方式有2种

1. 在零休时调低阻抗，该阻抗还应该是一个动态变化的阻抗
2. 在电弧电压稳定阶段，将接地电阻人为降为接近0试试

还有就是比较复杂的解决方案了，通过有限元积分法来算出电弧模型，那这是一个全新的挑战。

Github图床依旧不好用。

1. 建立武汉考核场基础PSCAD模型

1.1 供电电压

分析正常运行电压幅值，设置基地220kV电压为223kV。

运行电压，基本一致。

1.2 设置变压器及开关站端口电容。

2条馈线发生单相接地故障后，本身在空载状态容流非常小，可以认为测定到的全部为背景容流，有效值为4.072A。

计算得到电容量为0.743-0.081=0.662uF。

仿真容流如图所示，基本一致。

实测5.698A，仿真可的5.72A，基本相符。

1.3 考核场地网电阻

考虑故障相电压，故障后故障相电压为14V。

设置电阻为3.3Ω，仿真电压曲线如图。

基础模型设置完毕。

从另一个角度去计算地网故障过渡电阻。

记录馈线2的零序电流和故障相电压。

按照B相故障电压除以零序电流来计算B相接地阻抗，其值应等于接地电阻并联B相线路对地导纳。

接地电阻为固定值500Ω。

也许散流电阻会随着阻抗值以及系统电流值而变化，那么就需要建立土地模型了。

707V（实测）对应700V（仿真）；

3.5A（实测）对应3.38A（仿真）。

2. 考虑对地导纳的中性点电压数学模型

2.1 数学模型

利用简化公式，得到接地电流的计算公式

2.2 数据分析

利用这组数据来计算一下，网架结构是4条馈线空载。

利用135和002的录波数据进行分析。

以上这组数据很奇怪，发生B相接地故障之后，B相电压降低，A相电压居然也降低了一点，大致保持不变，而C相电压升高，这不符合理论，考虑到架空1回线的感应电压，预计是感应电引起的。容性电流的测量数据也比较奇怪，为什么是这么大？是所有线路容性电流之和呢？

换一组更干净的数据进行计算。

试一试这组，1、2、3馈线，架空1、2馈线带小电容器，电缆1带5档电容器，故障电阻为500Ω。

2.2.1 计算线路对地电容

首先计算线路对地电容，计算方法为在正常运行状态下，

计算每条馈线的电容，认为每条馈线的电容是对称的，可大约计算为：

馈线1 C=5uF；馈线2 C=2.5uF；馈线3 C=9.25uF。

则总并联馈线电容量为16.75uF。

按照上面手写的公式进行计算，计算得总的并联对地电阻r=935Ω。

2.2.2 计算接地阻抗公式

计算接地电阻公式得：

解这样一个方程，其有解条件为：

2.2.3 找另一组电容量的进行计算

1、2、3馈线带3+4档电容器。

计算馈线3的电容量C3=6.7uF

则总的每相电容量可近似看做C=14.2uF

对地电导不能简单套用之前的计算结果，因为很可能电容的自放电电阻会串进回路中，从而导致不同网架结构及电容档位下，对地导纳的不准确，再换一组试一下。

2.2.4 6档电容，和计算出940欧姆电阻组只有电容器组别不同

总电容量

馈线1 C=5uF；馈线2 C=2.5uF；馈线3 C=18.358uF。

则总并联馈线电容量为25.858uF。

基本接近。

那么是否可以认为，之前3+4档不准确是因为多并进了一组电容器的自放电电阻，导致总体对地电导增加呢？那么现在如何准确测量对地电导就是解决这个问题的最终方案了。

2.2.4.7 1000欧姆电阻，只带线路电容器

按照线路对地电阻940欧姆进行辨识，辨识电阻差20欧姆，可接受。

2.3 电弧的辨识

利用数据：两组小电容都带上第一次

相电势及零序电压曲线。

电阻值的变化曲线如图所示

可以看出，随着电弧发展，电阻是逐渐变小的。但可以根据不同组数据推得，放电绝缘恢复后，绝缘强度会加大。

建模中需用到可控电流源

《Modeling Study for High Impedance Fault Detection in MV Distribution System》

Cui T, Dong X, Bo Z, et al. Modeling study for high impedance fault detection in MV distribution system[C]//2008 43rd International Universities Power Engineering Conference. IEEE, 2008: 1-5.

DOI: 10.1109/UPEC.2008.4651507 

摘要

建模研究为高阻抗故障（HIF）检测的研究提供了一种更有效，更灵活的方法。 能够揭示HIF的大多数功能的准确模型非常重要。 在对记录的测试结果进行广泛研究的基础上，本文总结了一组最常见且令人满意的特征：电弧特征，非线性，随时间变化的电阻和随机性。 已经公开了可以重构这些特征的仿真建模方法。 利用ATP-EMTP模型，提出了一种基于一系列时变接地电阻和动态电弧电阻的HIF模型。 为了重建HIF的这些细节特征，已经测试了电弧参数及其影响。 随机因素已被引入该模型的HIF行为不稳定。最后，通过将该模型应用于模拟的MV系统，初步讨论了几种特征提取和检测方法。

1. Introduction

高阻抗故障（HIF）通常定义为导体在非导电表面上的不必要的电接触，从而限制了故障电流，使常规继电器的检测水平降低[1]。 由于HIF通常是由在公众范围内被压倒但通电的导体引起的，并且大多带有电弧，因此对人身安全和财产安全构成了巨大威胁。 因此，HIF检测早已成为保护工程师关注的重点。但这仍然是一个未解决的问题。

由于没有明显的稳态故障特征，因此基本的短路模型不适合HIF研究。因此，使用特殊的波形和故障电流/电压的不稳定行为来识别此类故障。 罗素与TAMU的研究人员进行了各种现场测试。 已经使用了谐波能量，频谱，电弧模式和随机性等HIF特征，并提出了一种具有专家系统的复合算法[2]。 在各种细节特征中，三次谐波匝数更加实用和独特，三次谐波的相位角和幅度被证明是HIF的独特特征[3] [4]，而大多数情况下，随机故障间歇是HIF的共同特征。 在大多数阶段测试中[2] [5]。

以前有关HIF检测的许多研究高度依赖于现场测试。 昂贵的阶段测试和不可预测的实验条件禁止在各种系统条件下对HIF进行全面研究。 因此，基于实际测试的结果，对于HIF检测的研究非常必要的是可以准确表示这些特征的数学模型。 已经提出了几种HIF模型：Nam通过使用时变电阻来拟合HIF来模拟HIF [6]，Michalik使用弧形模型来描述HIF的详细波形[7]，而Elkalashy也使用通用模型 表示HIF电弧故障特征的电弧模型[8]。

由于某些最显着的波形失真是由电弧引起的，例如周期性的失超，重燃，随机故障爆发，以及更大范围内的故障非线性。 弧模型的研究是HIF建模的方法。尽管HIF电弧与大多数电弧模型不同，后者专注于高压开关设计，超高压线路故障定位或自动重合闸系统[9]。 对于HIF，电弧通常位于不受限制的空间内，具有较短的长度和较低的系统电压。 因此，应指定弧的参数。

本文在对现场数据进行研究的基础上，对HIF的机理进行了分析和总结。 详细介绍了具有电弧热方程式和可变接地电阻的仿真模型。 弧模型参数是所提出模型的一个非常重要的方面。通过全面扫描弧的参数，可以重构HIF弧的不同行为并进行相应分类。 包括随机性和瞬态性在内的其他因素也旨在表示配电系统中HIF功能的更多功能。 利用随机因素，已经重建了间歇行为。 在使用分布式参数馈送器测试模型时，已揭示出HIF的快速瞬态功能。

本文的组织结构为：第二部分是现场测试数据和HIF机制的摘要； 使用ATP-EMTP进行建模的方法和模型的检验在第三部分中； 在第四节中，使用该HIF模型对MV系统进行了仿真，还初步揭示了一些功能。

2. HIF现场数据和机制

A. 现场数据

以下是从德州电力公司，台湾电力公司和TAMU的实际现场测试中借来的数字，它们代表了各种HIF阶段测试波形。 图1（a）和（b）说明了这些详细的波形失真。 图1（c）说明了较长时间范围内HIF的随机性。

上面的典型高阻抗故障电流图表明了HIF特性的不同方面：1）在详细范围内，过零电流附近的特定畸变是电弧[7] [8]的明显特征； 2）在每个周期的范围内，由于接地电阻非线性[3] [4]，波形看起来像正常的正弦波电流，由于谐波而失真。 3）在更长的时间范围内，HIF会以间歇性模式爆发并熄灭[2] [5]。

在各种文档中，这些功能被引用为HIF的最常见特征，因此已经开发出许多检测技术来利用这些功能。

B. HIF机制-电弧

尽管电流波形在以上不同情况下的行为有所不同，但仍有一些HIF的潜在机制有助于上述这些共同特征。 本文工作的目的是基于这些机制对HIF进行建模。 弧及其相应的影响在这些方面起着重要作用。

1）典型的电弧特征：与正常的短路故障不同，HIF产生的稳态电流有限，对于典型的12.5 kV系统，故障电流范围为10至50A [1]。 因此，弧的细节特征不再可忽略。 电弧实际上塑造了特殊的细节，例如穿越零淬火和故障电流的重新点火。

2）引起谐波失真的接地电阻的非线性也可以通过故障/电弧路径的热特性来简单地解释：当电流下降时，注入功率也下降，由于冷却而造成功率损耗， 故障路径将减小，从而使电流的绝对值低于相交零点附近的标准正弦波，因此，将谐波注入故障电流。

3）在大多数HIF情况下，电弧放电路径是在空气中且冷却条件较好的情况下进行的，这使电弧更容易熄灭，并导致HIF电流断断续续。其他事实（例如导体的随机摆动和电弧运动）也有助于HIF的间歇/随机功能。

如图1所示，并非每个HIF都具有所有这些特征，但是所有这些特征都导致了HIF的一个相对共同的组成部分：断层电弧，随机的熄灭/重击行为以及更大的接地电阻率。 而本文的HIF模型就是基于这些机制的。

3. HIF 建模

A. 用ATP-EMTP建立模型

在本节中，对10 kV系统中的典型HIF进行了分析和建模，通过选择具有适当参数设置的电弧模型以及在电弧模型中包括随机因素，可以实现上述空气电弧特性。

大多数HIF是单相接地故障[1]。 在故障点，HIF由两部分组成：1）导体与非导体之间的动态交流电弧； 2）故障路径电阻，通常是树木，建筑物或地面。因此，HIF模型可以由一系列两个可变电阻器来表示：瞬态电弧电阻器和稳态较高故障路径电阻器[6]。 前一个$R_{ARC}$描述了由电弧引起的每个周期的波形的细节（熄弧和重燃）。 后一个$R_P$表示根据接地电阻率和介电条件而变化的故障路径电阻。

由ATP-EMTP的不同MODELS模块控制的两个随时间变化的电阻已用于构建这两个电阻。

对于动态电弧电阻$R_{ARC}$，有多种建模方法。 黑匣子模型仅通过使用外部信息（例如电弧电流和电压）来描述电弧的电气特性，因此它们更适合于本研究。 Cassie模型和Mayr模型是最有代表性的电弧模型，它们基于具有相似思想的热方程：电弧电导与电弧放电路径中的热量有关，但是它们具有不同的恒定参数假设。 这两个模型及其推导已广泛用于电弧的研究，例如断路器，自动重合闸系统和故障定位的研究[9]。 对于我们对HIF弧的特定研究，选择了Mayr方程，因为它最适用于小电流，尤其适用于表示电弧过零点的特性。

Mayr方程是。

式中，$g$是单位长度的电弧电导。 $τ_m$是时间常数，表示电弧的温度惯性。 $P_m$是每长度电弧的功率损耗； $E$是每长度的弧径电势； $i$是电弧电流。 在这个方程中，电弧的热状态由两部分表示：热源是电能注入$E_i$； 热损失是假设的恒定功率损失$P_m$； 热条件对电导$g$的变化的影响具有一个以$τ_m$表示的时间延迟。

对于交流电弧，当电流在每个周期接近零，$Ei <P_m$时，电弧内部的热量将减少，电导$g$也将减少，由于时间常数$τ_m$，$g$的变化将滞后。 因此，从当前的零交叉点开始会有最低电导点的延迟，从而使电弧持续存在，并在每个周期内都围绕零交叉点出现灭弧和重燃。

另外，谐波，特别是具有特定相位的三次谐波也可以简单地进行解释：如果三次谐波都过零时与基波相比的相位大约为180º，则三次谐波会减弱基波电流，使其低于理想正弦波 在零点附近波动。 这也是公式（1）的意义。

对于上述典型的Mayr电弧模型，具有更长的时间延迟$τ_m$和更低的功率损耗$P_m$（较差的冷却条件），电弧将更可能稳定持续。 矛盾的是，更好的冷却条件意味着，由于较低的$τ_m$和较高的$P_m$，排出路径内部的热量将更快地散发。 因此，在更好的冷却条件下，电弧可能更容易完全自熄。 通常，Mayr的模型用于有限空间（开关室）中的断路器设计。 对于露天故障电弧，冷却条件（$τ_m$和$P_m$）和电弧形状（由电弧长度表示）是可变的，应加以调整。 而且，露天的更好的冷却条件将使电弧更容易熄灭。 这导致了随机性特征。

对于状态稳定电阻$R_P$，本文估算的主要考虑因素是接地电阻率，该值随土壤类型，温度，湿度和许多其他因素而变化。 典型的接地电阻率ρ从中等水平的300Ωm（在页岩中）到非常高的水平（在粗砂中）[3000]变化[12]。 假设故障点处的HIF由半径为$r_1 = 5 cm$的圆柱电极表示。接地电阻可以通过$R =ρ/（2πr_1）$来计算。 电阻值的范围为1kΩ至10kΩ。因此，在此模型中，$R_P$的变化范围为10kΩ至5kΩ，并沿时间轴变化。

对于使用EMTP的MODELS进行建模，从电源电路中获取电弧的电压和电流，并在每个模拟步骤中将其馈入MODELS的输入，然后根据这些输入，通过以下方式，MODELS可以用于求解（1）：

$t_0$是故障开始时间，$t$是当前仿真时间。 $Δt$是时间步长。 订阅t表示当前时间步的数据，t –Δ t表示最后计算步的历史数据。 然后，结果g将在下一个模拟步骤中作为可变电弧电阻应用于电源电路。

B. HIF模型结果的示例

下图是一个HIF模型的电弧电流示例的结果，考虑到室外的冷却条件，电弧功率损耗$P_m$设置为8 kW / m（正常值为3 kW / m），电弧 长度为5厘米，时间常数$τ_m$设置为600us。

图3中的电压和电流的测量是在弧点处进行的。 但是，对于位于母线的故障检测器，由于较低的电弧电压和较高的路径阻抗，因此难以获得准确的电弧电压。 对于平衡接地系统，该电弧电流可以在相线接地故障的情况下从中性线电流获得。

C. 测试和辨识电弧参数

对于此动态电弧模型，三个参数：$P_m$，$τ_m$和电弧长度确定它是自熄电弧还是稳定持续电弧，并且这些参数还会导致HIF电流的形状不同以及电弧畸变程度。

具有更好的冷却条件：更大的功率损耗或更低的延时，HIF电弧往往更容易熄灭。

在图4中，当电流过零时，HIF电弧电流消失，这种机制有助于实现HIF电弧最常见的间歇性特征。

通过不同的参数，此HIF电弧电流的形状会发生变化，如图5所示。

对于持续稳定的电弧，周期性失真将随着功率损耗的增加和/或时间常数的减小而增加。 换句话说，在更好的冷却条件下变形会更高。

此外，如前所述，如果冷却条件达到更高的水平，电弧可能会自行熄灭。 通过在10 kV交流电压源下扫描该模型的所有三个参数，下图显示了熄灭和持续电弧放电情况的边界。

在图6中，右下方是“电弧稳定持续”参数区域：较低的功率损耗和较高的时间常数表示较差的冷却条件。 相反，左上方的“电弧自熄”参数区具有更好的冷却条件，电弧将在爆裂后几个周期在零交叉点处自熄。 如图1（c）所示，随机重发会导致间歇性中断。 此外，如图5所示，参数在边界附近的持续弧似乎具有较高的周期性失真。

D. 修正（随机因素）

由于复杂的现场情况，这三个电弧参数是可变的。 因此，通过将随机因素引入这些参数，开发了一种HIF模型，旨在重建第二节中的随机特征。

在图6中，当将正常参数设置在持久区域的边界附近，并在这些参数之一中引入随机偏差时，可以描述随机间歇但仍具有详细弧特征的波形：

在图7中，时间常数设置为$τ_m = 600us·（1±0.25·Rnd）$，其中Rnd是由EMTP生成的均匀分布的随机数，范围为0到1。$P_m = 9 kW / m$， 弧长为5 cm，位于图6中的边界之一。 电流过零后的每半个周期，将产生一个新的$τ_m$，为下一次电流过零做准备。

通过这种方式，HIF弧模型具有详细特征以及间断/随机特征。 在下一部分中，此模型用于模拟MV系统中，以进一步提取特征。

4. 系统仿真及检测方法

A. 系统仿真

本节采用中性点接地系统。 使用HIF模型模拟相接地HIF。

主要采样的模拟信号是零线电流，在平衡的接地系统中，该零线电流被认为等于相线对地电流。

HIF在具有线性R-L型负载的20公里架空线中间进行。 分布式参数用于表示HIF的瞬态特征。

故障电流的结果在图9中。 这些重要和最常见的特征已由该模型揭示：1）随机爆发并熄灭； 2）电弧熄灭和点燃； 3）周期性失真或谐波； 4）此外，在实际的分布式参数系统中，以较高的采样速度，可以捕获由故障传导的初始引起的快速瞬变，并且可以用作另一个独特的特征。

B. 特征提取

小波分解已被用于通过电弧熄灭和重燃来提取细节失真，类似的小波和处理方法已在[13]中进行了详细介绍。

频率限制为1 kHz至10 kHz的带通滤波器用于提取HIF的快速瞬态特征。

根据[3] [4]，谐波特征主要由三次谐波与基波的相位差以及与基波的比表示。

5. 结论

与昂贵的现场测试相比，通过建模进行的HIF检测研究是一种更有效，更灵活的方法。 本文通过对高阻抗电弧故障机理的研究，利用ATP-EMTP模型对细节波形以及间歇性特征进行了解释和重构。通过将此模型应用于分发系统，一些最独特的功能已经被揭示出来。 最后，提出了几种初步的方法作为特征提取的一个例子。

参考文献

[1] PSRC Working Group D15, “High Impedance Fault Detection Technology,” Report of PSRC. March 1, 1996. [Online]. Available: http://grouper.ieee.org/groups/td/dist/documents/highz.pdf .

[2] R. Patterson, W. Tyska, B. D. Russell, and B. M. Aucoin, “A Microprocessor-Based Digital Feeder Monitor with High-Impedance Fault Detection,” in 47th Annual Conference for Protective Relay Engineers Texas A&M University, College Station, Texas, USA, 1994.

[3] A. E. Emanuel, D. Cyganski, J. A. Orr, S. Shiller, and E. M. Gulachenski, “High impedance fault arcing on sandy soil in 15 kV distribution feeders: contributions to the evaluation of the low frequency spectrum,” Power Delivery, IEEE Transactions on, vol. 5, pp. 676-686, 1990.

[4] D. I. Jeerings and J. R. Linders, “Unique aspects of distribution system harmonics due to high impedance ground faults,” Power Delivery, IEEE Transactions on, vol. 5, pp. 1086-1094, 1990.

[5] C. L. Benner and B. D. Russell, “Practical high-impedance fault detection on distribution feeders,” Industry Applications, IEEE Transactions on, vol. 33, pp. 635-640, 1997.

[6] S. R. Nam, J. K. Park, Y. C. Kang, and T. H. Kim, “A modeling method of a high impedance fault in a distribution system using two series time-varying resistances in EMTP,” in Power Engineering Society Summer Meeting, 2001. IEEE, 2001, pp. 1175-1180 vol.2.

[7] M. Michalik, W. Rebizant, M. Lukowicz, Seung-Jae Lee, and SangHee Kang, “High-impedance fault detection in distribution networks with use of wavelet-based algorithm,” Power Delivery, IEEE Transactions on, vol. 21, pp. 1793-1802, 2006.

[8] N. I. Elkalashy, M. Lehtonen, H. A. Darwish, M. A. Izzularab, and A. M. I. Taalab, “Modeling and experimental verification of high impedance arcing fault in medium voltage networks,” Dielectrics and Electrical Insulation, IEEE Transactions on [see also Electrical Insulation, IEEE Transactions on], vol. 14, pp. 375-383, 2007.

[9] Y. Li, X. Dong, Z. Q. Bo, N. F. Chin, and Y. Ge, “Adaptive reclosure using high frequency fault transients,” in Developments in Power System Protection, 2001, Seventh International Conference on (IEE), 2001, pp. 375-378.

[10] A. A. Girgis, W. Chang, and E. B. Makram, “Analysis of highimpedance fault generated signals using a Kalman filtering approach,” Power Delivery, IEEE Transactions on, vol. 5, pp. 1714-1724, 1990.

[11] H. Shyh-Jier and H. Cheng-Tao, “High-impedance fault detection utilizing a Morlet wavelet transform approach,” Power Delivery, IEEE Transactions on, vol. 14, pp. 1401-1410, 1999.

[12] “IEEE guide for measuring earth resistivity, ground impedance, and earth surface potentials of a ground system” IEEE Std 81-1983, 1983.

[13] Xinzhou Dong, Yaozhong Ge, Jiali He, “ Surge impedance relay,” Power Delivery, IEEE Transactions on, vol. 20, pp. 1247-1256, Apr. 2005.

Write Level-2 MATLAB S-Functions

From：https://ww2.mathworks.cn/help/simulink/sfg/writing-level-2-matlab-s-functions.html

About Level-2 MATLAB S-Functions

使用Level-2MATLAB®S函数API，您可以使用MATLAB语言来创建具有多个输入和输出端口的自定义块，并能够处理Simulink®模型产生的任何类型的信号，包括任何数据的矩阵和帧信号 类型。 2级MATLAB S函数API与创建C MEX S函数的API紧密对应。 创建C MEX S函数的许多文档也适用于Level-2 MATLAB S函数。 为避免重复，本节着重于提供特定于编写Level-2 MATLAB S函数的信息。

Level-2 MATLAB S-function是MATLAB函数，用于定义在Simulink模型中引用MATLAB函数的Level-2 MATLAB S-Function块实例的属性和行为。 MATLAB函数本身包含一组回调方法（请参见Level 2 MATLAB S-Function回调方法），Simulink引擎在更新或仿真模型时会调用这些方法。 回调方法执行初始化和计算由S函数定义的块的输出的实际工作。

为了完成这些任务，引擎将运行时对象作为参数传递给回调方法。 运行时对象有效地充当了S功能块的MATLAB代理，从而允许回调方法在仿真或模型更新期间设置和访问块属性。

About Run-Time Objects（关于运行对象）

Simulink引擎调用Level-2 MATLAB S函数回调方法时，会将Simulink.MSFcnRunTimeBlock类的实例作为参数传递给该方法。 该实例被称为S-Function块的运行时对象，对于Level-2 MATLAB S-function回调方法具有相同的目的，而SimStruct结构则用于C MEX S-function回调方法。 该对象使该方法能够提供并获得有关块端口，参数，状态和工作矢量的各种元素的信息。 该方法通过获取或设置块运行时对象的属性或调用方法来执行此操作。 有关获取和设置运行时对象属性以及调用运行时对象方法的信息，请参见Simulink.MSFcnRunTimeBlock类的文档。

运行时对象不支持MATLAB稀疏矩阵。 例如，如果变量块是运行时对象，则Level-2 MATLAB S函数中的以下行会产生错误：

block.Outport(1).Data = speye(10);

speye命令形成一个稀疏身份矩阵。

Level-2 MATLAB S-Function Template（Level 2 MATLAB S函数模板）

使用基本的Level-2 MATLAB S函数模板msfuntmpl_basic.m来开始创建新的Level-2 MATLAB S函数。 该模板包含由Level-2 MATLAB S-function API定义的所需回调方法的框架实现。 要编写更复杂的S函数，请使用带注释的模板msfuntmpl.m。

要创建MATLAB S函数，请制作一个模板副本，并根据需要编辑该副本，以反映您正在创建的S函数的所需行为。 以下两节描述了MATLAB代码模板的内容。 编写Level-2 MATLAB S-Function的示例部分介绍了如何编写对单位延迟建模的2级MATLAB S函数。

Level-2 MATLAB S-Function Callback Methods（2级MATLAB S函数回调方法）

2级MATLAB S函数API定义了构成2级MATLAB S函数的回调方法的签名和一般用途。 S函数本身提供了这些回调方法的实现。 所述实现又确定块属性（例如，端口，参数和状态）和行为（例如，块输出作为时间的函数以及块输入，状态和参数）。 通过使用一组适当的回调方法创建S函数，您可以定义满足应用程序特定要求的块类型。

一个2级MATLAB S函数必须包括以下回调方法：

• 用于初始化基本S函数特征的设置函数
• 一个用于计算S函数输出的Outputs函数

根据S函数定义的块的要求，您的S函数可以包含其他方法。 Level 2 MATLAB S函数API定义的方法通常对应于C MEX S函数API定义的类似命名的方法。 有关在仿真过程中何时调用这些方法的信息，请参见Simulink Engine与CS功能交互中的“过程视图”。

下表列出了所有2级MATLAB S函数回调方法。

Using the setup Method（使用设置方法）

Level 2 MATLAB S-function中设置方法的主体将初始化相应Level-2 MATLAB S-Function块的实例。 在这方面，设置方法类似于C MEX S函数实现的mdlInitializeSizes和mdlInitializeSampleTimes回调方法。 设置方法执行以下任务：

• 初始化块的输入和输出端口数。
• 设置这些端口的属性，例如维度，数据类型，复杂性和采样时间。
• 指定块采样时间。 有关如何指定有效采样时间的更多信息，请参见《使用Simulink》中的“指定采样时间”。
• 设置S功能对话框参数的数量。
• 通过将MATLAB S函数中的局部函数的句柄传递给S函数块的运行时对象的RegBlockMethod方法来注册S函数回调方法。 有关使用RegBlockMethod方法的信息，请参见Simulink.MSFcnRunTimeBlock的文档。

Example of Writing a Level-2 MATLAB S-Function（一个例子）

以下步骤说明了如何编写简单的Level-2 MATLAB S函数。 如果适用，这些步骤包括模型msfcndemo_sfundsc2中使用的S函数示例msfcn_unit_delay.m中的示例。 所有代码行都将变量名称块用于S函数运行时对象。

1 将Level 2 MATLAB S函数模板msfuntmpl_basic.m复制到您的工作文件夹中。 如果在复制文件时更改了文件名，请将功能行中的功能名更改为相同的名称。

2 修改设置方法以初始化S函数的属性。 对于此示例：

• 将运行时对象的NumInputPorts和NumOutputPorts属性设置为1，以初始化一个输入端口和一个输出端口。
• 调用运行时对象的SetPreCompInpPortInfoToDynamic和SetPreCompOutPortInfoToDynamic方法，以指示输入和输出端口从模型继承其已编译属性（尺寸，数据类型，复杂度和采样模式）。
• 将运行时对象的InputPort的DirectFeedthrough属性设置为false，以指示输入端口没有直接馈通。 保留在模板文件副本中设置的所有其他输入和输出端口属性的默认值。 为Dimensions，DatatypeID和Complexity属性设置的值将覆盖使用SetPreCompInpPortInfoToDynamic和SetPreCompOutPortInfoToDynamic方法继承的值。
• 将运行时对象的NumDialogPrms属性设置为1，以初始化一个S函数对话框参数。
• 通过将运行时对象的SampleTimes属性的值设置为[-1 0]，指定S函数具有继承的采样时间。

• 调用运行时对象的RegBlockMethod方法来注册此S函数中使用的以下四个回调方法。

  • PostPropagationSetup
  • InitializeConditions
  • Outputs
  • Update

  从模板文件的副本中删除所有其他注册的回调方法。 在对RegBlockMethod的调用中，第一个输入参数是S函数API方法的名称，第二个输入参数是MATLAB S函数中关联的局部函数的函数句柄。

  下面这个msfcn_unit_delay.m的例子，描述上面所述的步骤：

function setup(block)

%% Register a single dialog parameter
block.NumDialogPrms  = 1;

%% Register number of input and output ports
block.NumInputPorts  = 1;
block.NumOutputPorts = 1;

%% Setup functional port properties to dynamically
%% inherited.
block.SetPreCompInpPortInfoToDynamic;
block.SetPreCompOutPortInfoToDynamic;

%% Hard-code certain port properties
block.InputPort(1).Dimensions        = 1;
block.InputPort(1).DirectFeedthrough = false;

block.OutputPort(1).Dimensions       = 1;

%% Set block sample time to [0.1 0]
block.SampleTimes = [0.1 0];

%% Register methods
block.RegBlockMethod('PostPropagationSetup',@DoPostPropSetup);
block.RegBlockMethod('InitializeConditions',@InitConditions);
block.RegBlockMethod('Outputs',             @Output);  
block.RegBlockMethod('Update',              @Update);  

如果您的S函数需要连续状态，请使用运行时对象的NumContStates属性在设置方法中初始化连续状态的数量。 不要在设置方法中初始化离散状态。

3 在PostPropagationSetup方法中初始化离散状态。 2级MATLAB S函数将离散状态信息存储在DWork向量中。 在此示例中，模板文件中的默认PostPropagationSetup方法就足够了。

msfcn_unit_delay.m中的以下PostPropagationSetup方法名为DoPostPropSetup，它初始化了一个名为x0的DWork向量

function DoPostPropSetup(block)

%% Setup Dwork
  block.NumDworks = 1;
  block.Dwork(1).Name = 'x0'; 
  block.Dwork(1).Dimensions      = 1;
  block.Dwork(1).DatatypeID      = 0;
  block.Dwork(1).Complexity      = 'Real';
  block.Dwork(1).UsedAsDiscState = true;

如果您的S函数使用其他DWork向量，则也应在PostPropagationSetup方法中对其进行初始化（请参见在Level 2 MATLAB S函数中使用DWork向量）。

4 在InitializeConditions或Start回调方法中初始化离散和连续状态或其他DWork向量的值。 对于模拟开始时一次初始化的值，请使用Start回调方法。 每当重新启用包含S功能的已启用子系统时，请使用InitializeConditions方法获取需要重新初始化的值。

  对于此示例，使用InitializeConditions方法将离散状态的初始条件设置为S函数的dialog参数的值。 例如，msfcn_unit_delay.m中的InitializeConditions方法为：

	function InitConditions(block)

  %% Initialize Dwork
  block.Dwork(1).Data = block.DialogPrm(1).Data;

对于具有连续状态的S函数，请使用ContStates运行时对象方法初始化连续状态数据。 例如：

block.ContStates.Data(1) = 1.0;

5 在Outputs回调方法中计算S函数的输出。 对于此示例，将输出设置为DWork向量中存储的离散状态的当前值。

  msfcn_unit_delay.m中的Outputs方法为：

	function Output(block)

  block.OutputPort(1).Data = block.Dwork(1).Data;

6 对于具有连续状态的S函数，请使用“导数”回调方法计算状态导数。 运行时对象将派生数据存储在其“派生”属性中。 例如，以下行将第一状态导数设置为等于第一输入信号的值。

block.Derivatives.Data(1) = block.InputPort(1).Data;

本示例不使用连续状态，因此不实现“派生”回调方法。

7 在Update回调方法中更新所有离散状态。 对于此示例，将离散状态的值设置为第一输入信号的当前值。   msfcn_unit_delay.m中的Update方法是：

	function Update(block)

  block.Dwork(1).Data = block.InputPort(1).Data;

8 在Terminate方法中执行任何清除操作，例如清除变量或内存。 与C MEX S函数不同，Level-2 MATLAB S函数不需要具有Terminate方法。

有关其他回调方法的信息，请参见Level 2 MATLAB S函数回调方法。 有关运行时对象属性的列表，请参见Simulink.MSFcnRunTimeBlock和父类Simulink.RunTimeBlock的参考页。

Instantiating a Level-2 MATLAB S-Function

要在模型中使用Level-2 MATLAB S-function，请将Level-2 MATLAB S-Functionblock的实例复制到模型中。 打开该块的“块参数”对话框，然后在S函数名称字段中输入实现S函数的MATLAB文件的名称。 如果您的S函数使用任何其他参数，请在“块参数”对话框的“参数”字段中以逗号分隔的列表形式输入参数值。

Operations for Variable-Size Signals（可变大小信号的操作）

以下是对2级MATLAB S函数模板（msfuntmpl_basic.m）的修改以及允许您使用可变大小信号的其他操作。

function setup(block)
% Register the properties of the output port
block.OutputPort(1).DimensionsMode = 'Variable';
block.RegBlockMethod('SetInputPortDimensionsMode',  @SetInputDimsMode);

function DoPostPropSetup(block)
%Register dependency rules to update current output size of output port a depending on
%input ports b and c
block.AddOutputDimsDependencyRules(a, [b c], @setOutputVarDims);

%Configure output port b to have the same dimensions as input port a
block.InputPortSameDimsAsOutputPort(a,b);

%Configure DWork a to have its size reset when input size changes.
block.DWorkRequireResetForSignalSize(a,true);

function SetInputDimsMode(block, port, dm)
% Set dimension mode
block.InputPort(port).DimensionsMode = dm;
block.OutputPort(port).DimensionsMode = dm;

function setOutputVarDims(block, opIdx, inputIdx)
% Set current (run-time) dimensions of the output
outDimsAfterReset = block.InputPort(inputIdx(1)).CurrentDimensions;
block.OutputPort(opIdx).CurrentDimensions = outDimsAfterReset;

Generating Code from a Level-2 MATLAB S-Function（从2级MATLAB S函数生成代码）

为包含Level-2 MATLAB S函数的模型生成代码要求您提供相应的目标语言编译器（TLC）文件。 您不需要TLC文件即可加速包含Level-2 MATLAB S函数的模型。 Simulink Accelerator™软件以解释模式运行Level-2 MATLAB S函数。 但是，如果M文件S函数在模型参考中，则M文件S函数无法在加速模式下使用。 有关为MATLAB S函数编写TLC文件的更多信息，请参见内联S函数（Simulink Coder）和内联MATLAB File S函数（Simulink Coder）。

MATLAB S-Function Examples

Level 2 MATLAB S函数示例提供了一组自文档模型，这些模型说明了Level 2 MATLAB S函数的用法。 在MATLAB命令提示符下输入sfundemos以查看示例。

MATLAB S-Function Limitations

• 2级MATLAB S函数不支持过零检测。
• 您不能从2级MATLAB S函数中触发函数调用子系统。

“中国人在自然科学方面的知识平均水平很低” “外国人水平都很高吗，你舔什么外国人？” 逻辑谬误：稻草人，红鲱鱼，诉诸动机

“中国人在自然科学方面的知识平均水平很低” “中国发展这么快你装看不见？” 逻辑谬误：推不出，一厢情愿

“中国人在自然科学方面的知识平均水平很低” “那怎么能有屠呦呦杨振宁？” 逻辑谬误：诉诸细节，烟雾弹

“中国人在自然科学方面的知识平均水平很低” “一个臭名昭著的大V也这么说” 逻辑谬误：希特勒归谬

“中国人在自然科学方面的知识平均水平很低” “科学不是中国人发明的不需要学，自古以来” 逻辑谬误：非我所创，诉诸年代，诉诸传统

正常人的讨论问题方法：

“中国人在自然科学方面的知识平均水平很低”

“你说的不对，中国人在自然科学知识的平均水平并不低，你说低是说外国人高吗”

“不是，平均水平取决于各个受教育水平的人群的分布统计，以及外国是个错误的概念，各个国家肯定不同”

“你做过什么统计了吗，凭什么说？”

“全国普通高中入学率约50-60%，再考虑文理分科，你可以估算接受高中理科教育的人占某个年龄的比例，但这只是近20年可用的估算方法。我国从1986年开始义务教育，1992年十四大提出目标世纪末基本扫除青壮年文盲，因此你可以大概估算95%以上超过四十岁的中国公民在自然科学方面都是文盲。”

“这也是没办法，历史原因，我们还在发展”

“你说得对，所以我说，中国人在自然科学方面的知识平均水平很低。”

在编写S-function时报错。

error occurred while running the simulation and the simulation was terminated Caused by: Output returned by S-function ‘cassie’ in ‘basic9/Cassie arc model sfunction/S-Function’ during flag=3 call must be a real vector of length 1

可能的错误因素：

1. 输出元素个数和你的定义输出个数不同；
2. s-function的输入变量个数和与其连接的模块的输入变量个数不一致；
3. 还有一种可能是输出为无穷，也就是除以0了；
4. S-function的输入变量的维数不是1维的向量；

电力系统的精确仿真，尤其是电磁暂态的精确仿真，更尤其是配电网层次的精确仿真，综合着细节，又综合着大尺度，这样的仿真是不是不可能做得出来啊！！！