一组典型的输电线路行波故障波形

2026-10-03 19:05:26

215

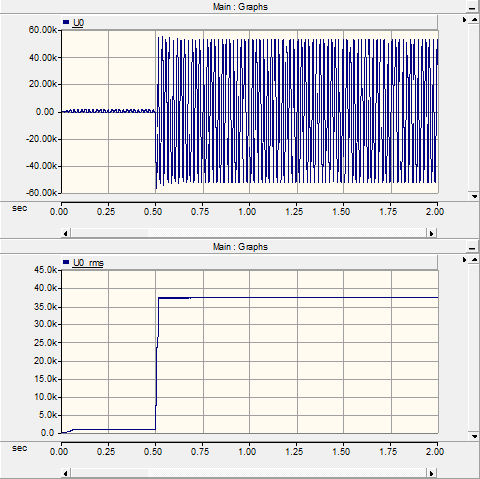
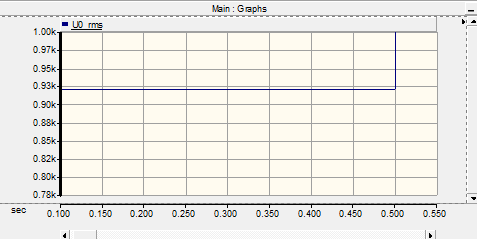
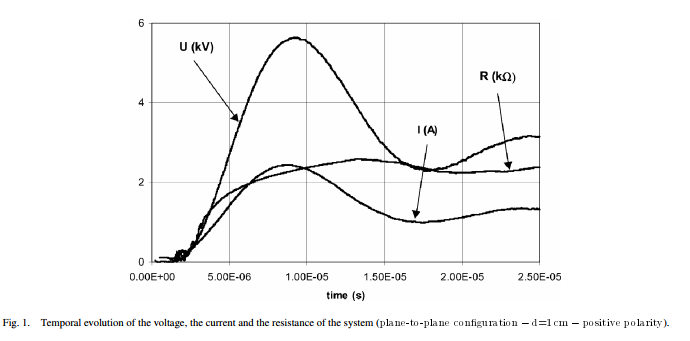
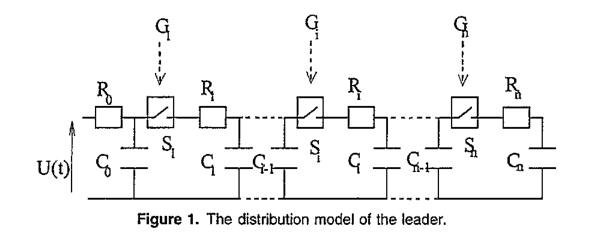
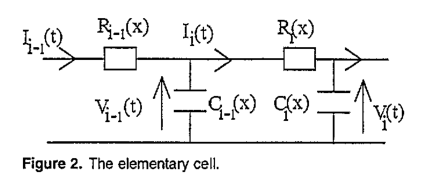
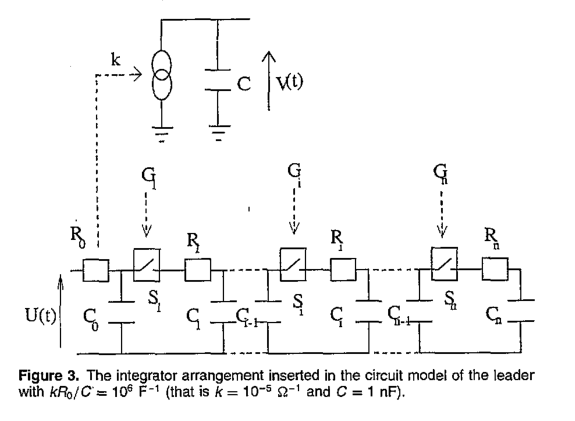
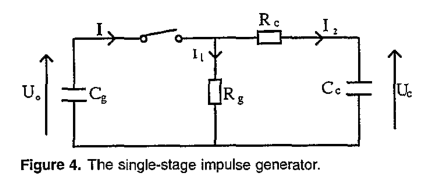
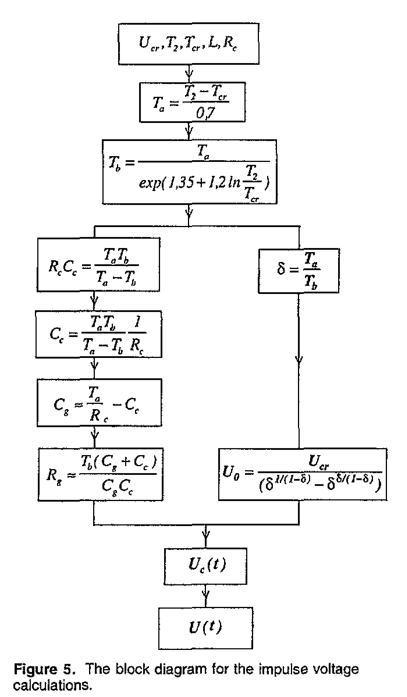
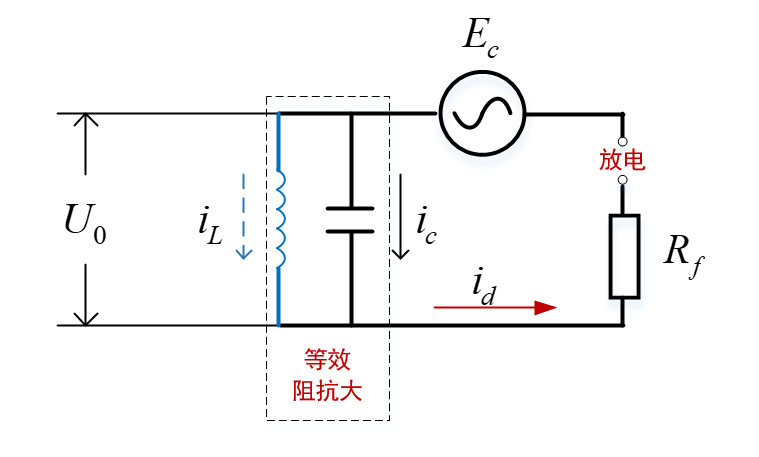
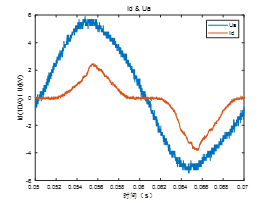
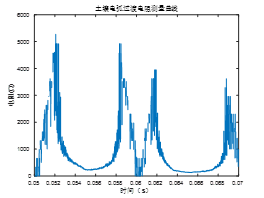
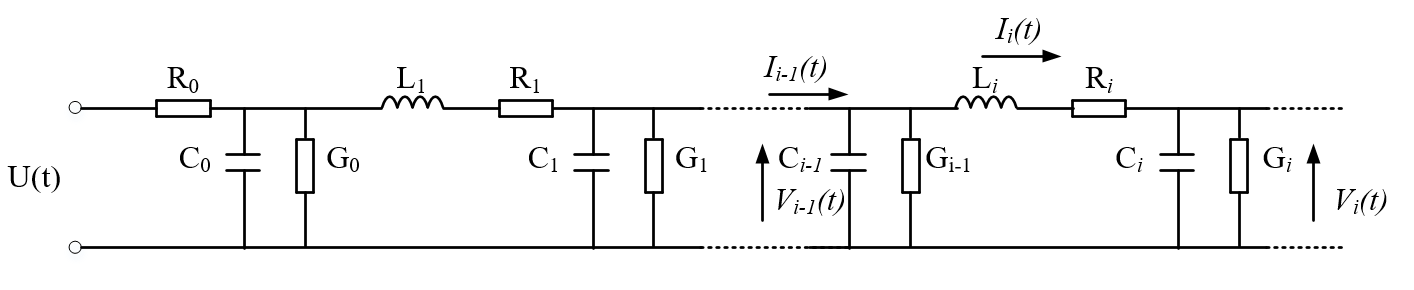
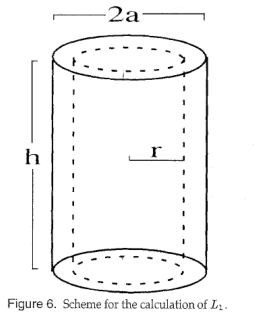
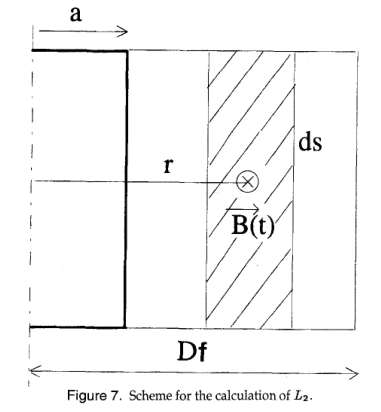
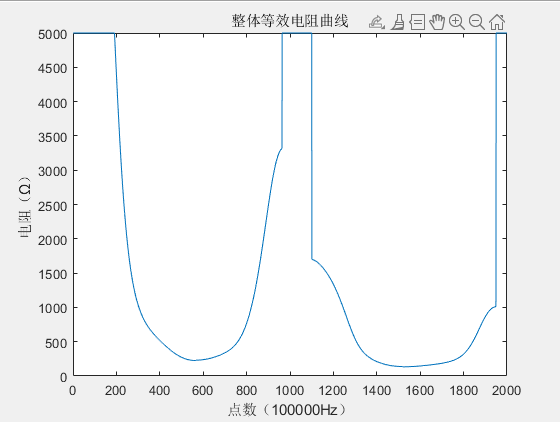
4. Conclusions on the Fault Loop Impedance on Crossbonded Cable Systems for Fault Location Purposes

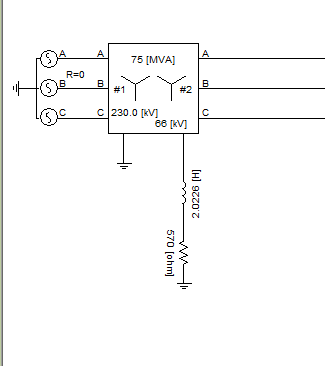
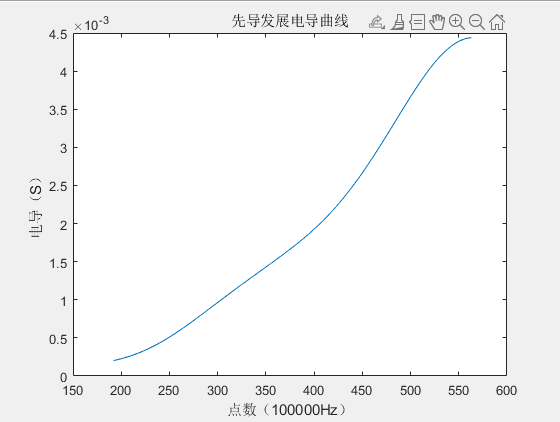
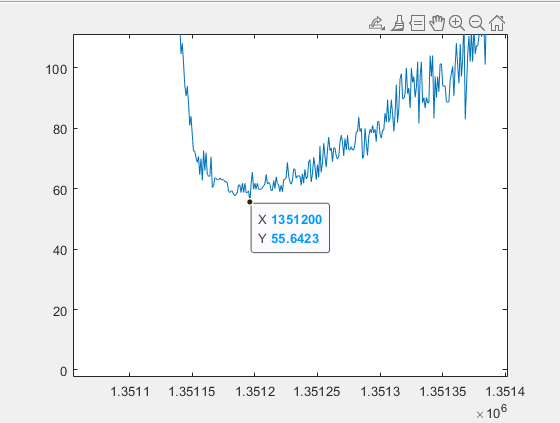
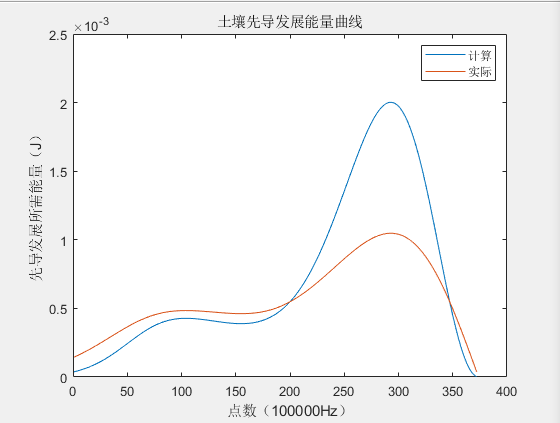
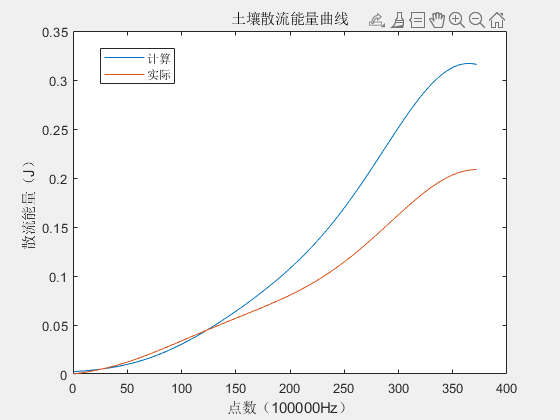
本章研究交联电缆故障回路阻抗的特性。结果表明，零序系统的建模对准确计算结果是非常重要的，并且有必要对护套系统进行详细描述。 然而，所有主要影响故障回路阻抗的参数都是电缆及其敷设配置的特定参数，其中描述接地和接地电阻的参数不太重要。 如果主导参数是公知的，并且如果包括护套的交联的详细模型在与真实的寿命相比时可以提供良好的结果，则可以训练基于人工智能的故障定位算法中的几个以在交联电缆上执行准确的故障定位。 如果模型不能做到这一点，人工神经网络不能产生良好的结果相比，现实生活中的故障阻抗。

据评估，一个实际实施的阻抗为基础的故障定位方法的混合线路是不可能实现的，如果高精度的要求。不同线路参数使不同线路类型的故障回路阻抗有很大差异，因此，架空线路参数的小误差给予电缆区段故障时的故障回路阻抗的大偏差。

最近要给玲珑报名乐器课程，钢琴是其中的选项之一，那么到底是买电钢琴还是真钢琴这是困扰众多家长的重要问题。

在搜集到了一些资料的前提下，能够得到如下结论供参考。

首先看预算，其次看目的。

1. 预算足够，看空间，如果能放得下，当然买三角钢琴，如果能放得下三角钢琴，那么一般也不会有练琴扰民的困扰；
2. 预算足够，空间不够，如果不担心扰民，那么可以买好的立式钢琴；如果担心扰民，则可以买静音钢琴或者混合电钢琴；
3. 预算不上不下，3万是可分界线，在这个价位上，可以考虑二手立式钢琴，或者混合电钢琴；
4. 预算不够，那么果断电钢琴。
5. 上面说的预算是只不影响家庭生活的轻轻松松的预算，而不是咬牙紧衣缩食的预算。

虽然上面已经包含了一些目的性，也要看孩子天赋，是否要走专业的钢琴道路。我个人认为，除非孩子表现出了极强的天赋或者家长是这行的从业人员。那么但无论哪种情况，除非预算相当充足，从电钢琴入门是比较好的选择。

主要有如下原因

1. 跟真钢琴相比，普通电钢琴的弱点在于击键的行程上的质感会有些许不完美，这在弹奏古典乐曲，需要表达感情变化的时候，可能会表现力不足，但这属于钢琴的高端玩法，初学期实在的体现不出太大区别；
2. 3万块的混合电钢琴的质感和真钢是一模一样的，但音色要远好于3万块的真钢，当然买二手的真钢也行；
3. 相对便宜的电钢琴，如几千块的电钢的击键的质感已经可以满足初学者练习的目的；
4. 电钢除了便宜和音色好（需戴耳机）外，体积小，不扰民是它的两项特别重要的优点。

综上所述，如果只是为了给孩子用于音乐启蒙，电钢琴是很不错的选择。

未完，后面在继续调研各个档位的电钢琴型号推荐。

1. 阻尼电阻的作用

阻尼电阻有2个主要作用，1是用于抑制中性点的位移电压，2是用于抑制系统可能发生的串联谐振，本质上讲二者是同一个事情。难点在于选取多大的阻尼电阻是合适的，过小的阻尼电阻无法有效抑制位移电压，而过大的阻尼电阻会抑制系统对故障识别的敏感度，也会影响系统电容电流监测算法的精确性。

具体内容见链接。

消弧线圈的阻尼电阻及其对系统的影响分析

时频流形稀疏重构：一种新的轴承故障特征提取方法

Time–frequency manifold sparse reconstruction: A novel method for bearing fault feature extraction

2. 理论背景

2.1 时频流形（TFM）学习

TFM 是 TF 域中的固有非线性流形结构，嵌入到有缺陷的轴承振动信号的 TFD 上，并且可以通过在重构相空间中对一系列 TFD 进行流形学习来提取 [12,13]。 TFM结合了非平稳信息和非线性信息，因此可以针对不同的振动信号显示不同的TF模式。 关于 TFM 技术的详细信息，读者可以参考[12]。

要学习 TFM，首先应通过相空间重构 (PSR) 技术在高维相空间中重构信号的流形。 对于具有 N 个数据点的信号 x(t)，m 维相空间中的第 i 个相位点向量给出为：

\[\mathbf{X}_{i}^{m}=\left[x_{i}, x_{i+\tau}, \ldots, x_{i+(m-1) \tau}\right] \tag{1}\]

其中$x_i$是$x(t)$的第i点数据，m是嵌入维数，$\tau$是延迟系数。对齐向量$ \left{\mathbf{X}_{i}^{m} \mid i=1,2,…,n}\right. $得到按时间顺序，时间相关的数据矩阵$ \mathbf{P} \in \mathrm{R}^{m \times n}(\tau=1, n=N-m+1) $在相空间中构造，其元素与 x(t) 具有以下关系：

\[P_{(j, k)}=x_{k+(j-1) \tau} \tag{2}\]

其中$j \in[1, m], k \in[1, n] .$

然后通过进行短时傅里叶变换 (STFT) 在 TF 域中表示相空间轨迹。 数据矩阵 P 的每一行（具有时间感）由 STFT 分析以提供 TF 表示，如以下等式所示：

\[\mathbf{S}_{j}(k, v)=\sum_{l=-\infty}^{\infty} \mathbf{P}_{j}[l] w[k-l] e^{-i \frac{2\pi}{Z} v l} \tag{3}\]

其中k和$v$分别是时间轴和频率轴的位置，Z是STFT中离散频点的个数，w(k)是短时分析窗口。 结果 $\mathbf{S}{j}(k, v)$为复数形式，也可以用两部分表示：幅度 $\mathbf{A}{j}(k, v)$和相位$\mathbf{\theta}_{j}(k, v)$。 幅度部分只是用于 TFM 学习的 TFD，相应的相位部分可以稍后用于 STFT 结果更新。 因此，可以从构建的数据 P 中生成 m 个 TFD，由 m 个大小为 $L \times n$的矩阵表示（L 为频点数，n 为时间点数）。

然后通过将上述 TFD 输入到流形学习算法中，在重建的相空间中计算 TFM。 在这一步中，使用局部切线空间对齐（LTSA）算法 [34] 来计算大小为 L?n 的 d（d 远小于 m）TFM。 有关 TFM 学习过程的更多详细信息，请参阅 [12]。 在本文中，第一个 TFM 签名被用作后续 TF 原子学习的图像。

Comsol等离子体模块使用手册

2. 等离子体模型所需数据

低温等离子体的建模不仅因为发生了大量的物理过程，而且还因为需要提供给模型的数据量很大，因此建模很困难。 本章概述了在尝试对等离子体建模之前需要收集的数据。

2.1 所需数据

本节概述了在尝试对等离子体建模之前要组装的数据。

主要困难之一是为感兴趣的等离子体找到完整且物理上正确的化学机制。 这可能只涉及少数反应和物种（如氩气），或者在分子气体的情况下，可能有数百个反应和数以百计的物种。 通常可以从文献搜索中找到化学机制，但如果它是一种独特的等离子体化学，那么化学机制可能是未知的。 唯一的选择是找到一种与您的特定应用具有相似特性的等离子体化学物质并将其用作参考。

以下部分将指导您了解构成等离子模型的每个特征的数据需求。

1. 建模

模型整体如下

主要参数，66kV系统，中性点不接地情况下的故障电流

放大

故障电流最大值为68.1A，有效值为48.15A。

正常运行的中性点电压有效值为625V，不平衡电压625/38105=1.64%

1.1 加入消弧线圈

加入消弧线圈2.0226H

1.2 加入阻尼电阻

最小值570Ω

非故障情况下，中性点电压930V

电阻性土壤中与放电有关的电学参数

Electrical Parameters Associated With Discharges in Resistive Soils

摘要

为了更好地了解电阻性土壤在大浪涌电流作用下的非线性行为，研究了电阻性土壤中与放电有关的电学参数。利用实验和计算方法，确定了土壤电阻率等与放电有关的参数。介电强度被发现是土壤含水量的函数，排泄引导场也是如此。测量了起始电流，实验结果与计算值吻合较好。

1. 引言

研究接地电极的土壤电离和放电过程的重要性主要是由于这些非线性现象降低了接地系统在大电流放电时的电阻。

尽管存在这种效应的实际后果，但目前对电阻性介质放电电学参数的实验数据很少，而且不同作者发表的参数之间的不同意见使得它们的值之间的比较成为一项相当困难的任务。

这就是为什么在提出评估程序之前，我们决定定义与可变电阻率土壤中的放电有关的最重要参数，例如介电强度、初始电流和放电导向场。为了阐明各参数在接地系统暂态电阻中的作用，提出了一套调节土壤流量参数的实验数据。

所有这些关键参数使我们能够更好地了解电阻性土壤中电放电的形成和发展。精确掌握这些参数有助于改善接地系统的设计，例如减少电力系统和建筑物的保护装置或对电磁干扰敏感的设备上的闪电所产生的沿海地区的暂态电阻。

整个实验测试是在实验室中进行的，使用小样本的电阻性土壤和浓缩电极。

2. 土壤电阻率的测定

土壤电阻率对接地系统的电阻起着决定性的作用。为了研究土壤中的电离现象，用浓缩电极进行了试验。由于接地电极极短，其感应行为可以忽略[12] ，因此接地电极周围的电场分布主要取决于土壤的电阻率和电流密度。

在这项研究中，考虑了大范围的电阻率，在50到500000Ωm之间。

提出了两种测定土壤电阻率的实验方法，这些土壤的特性如下:

• 其中石英占82.8% ，钾长石占2.9% ，石灰石占7.2% ，碳酸钙占3.1% ，云母占0.9% ，黑云母占2.4% ，磁铁矿占0.7% ;
• 黑色粘土;
• 由砂(50%)和粘土(50%)制成的混合物;
• 混凝土由$4.8dm^3$砂土，$1.6dm^3$水泥和$1dm^3$水组成。

经验中使用的土壤含水量按重量计约为0.06% 至15% 不等。

2.1 均匀电场法

实验是在平面对平面的间隙中进行的。电极表面为$72.4cm^2$，为了保持电场的均匀性，电极之间的距离不能超过1cm。

在所有的实验中，所使用的Marx发生器(600kV，4kJ)以8us个前沿时间(通常是第一次击穿雷电电流的时间)提供电流脉冲。快速电阻式分压器可以测量电压随时间的变化。电流测量采用与地平面串联的时间常数为0.35us的0.18Ω同轴分流器。

图1显示了含有未知电阻率沙子的系统的电压、电流和电阻的时间演化。

在这个例子中，仔细检查电压和电流记录，就会发现没有脉冲放电发展到缝隙中。因此，接地系统的电阻$R_t$定义为外加电位与阻性电流之比(线性条件)。但是测量到的电流$I$由阻性电流$I_r$和电容电流$I_c$的给出

\[I = Ir + Ic = Ir + C \frac { d U } { d t } \tag{1}\]

因此，为了忽略电容电流，$dU/dt = 0$确定了$R_t$的值。

知道这一电阻后，就可以使用众所周知的公式计算土壤电阻率。

\[R _ { t } = \rho \times \frac { d } { S } \tag{2}\]

我们得到

$\rho = 1600 \Omega \cdot m$

计算了几个电压等级的电阻率，最高可达8kV(超过此值，放电进入间隙并导致击穿)。看起来沙子的电阻率在这个电压范围内是恒定的。粘土和50%砂50%粘土的混合物也是如此。此外，混凝土的性能完全不同，如图2所示。

混凝土的电阻率随外加电场的增大而减小，表现出非线性。

虽然测量的土壤电阻率(砂、粘土和混合物)在8kV以下保持不变，但这种方法不允许在较高电压下评估这一特性。

为了阐明这一重要课题，我们提出了一种实验方法，用于测量高电压下土壤的电阻率。

Modelling of the leader current with an equivalent electrical network

长间隙先导电流等效电气网络模型

摘要

本文的目的是提出一种先导电流的电学模型，该模型与描述振荡冲击电压产生的电流有关。该模型允许评估沿先导通道的先导电流、电荷和电位分布。引线的物理参数用等效网络来描述。通过将这些参数积分到测试电路中，我们能够推导出气隙中任一点的电流和电荷，然后将我们的结果与实验产生的大气隙放电的实验结果进行了比较。该模型给出的电流和电荷特性与实验结果吻合较好。

1. 引言

气体排放中发生的基本过程过去是，现在仍然是许多研究的主题(Les Renardikres group 1972,1974,1977，Meek and Graggs 1978，Gary er A1 1984，Gallimberti 1979)。气体放电的物理机制非常复杂。它们取决于许多物理和几何参数，例如电极间隙。在这项工作中，较长的气隙是首要考虑的问题。在这样的空隙中发生的现象可以概括为以下几个方面。

放电在产生适当位置的自由电子的时间滞后之后开始。第一个电晕代表了第一个可观察到的电离过程，通常采取丝状通道或流光的形式。在某些情况下，第一次日冕之后是一个或多个暗期。

第二个可观察到的现象发生在第一次日冕之后。这是一个直径几毫米的电离通道，很热，是一个相对好的导体：引线。在它的顶端，产生了一个新的日冕，显示出一些丝状结构的证据，这种结构使先导通道前面的空气电离。正是通过这种机制，维持了显影放电中的电流流动，改变了间隙中的电场分布。随着外加电压的增加，引线沟道沿平面方向增长。

先导传播的最后阶段被称为“最后一跳”。这是引线传播的终端状态，其特征是电流迅速增加(回程)，这不可避免地会导致间隙短路。

许多工作致力于分析表征放电的不同参数，如电流、电荷、传播模式、速度和辐射电磁场。

了解放电电流是非常重要的，特别是在评估遭受直接撞击(例如触电、起火和损坏电气设备)的系统中可能发生的损坏时。 此外，电流还会辐射电磁场。众所周知，这些辐射场与工程系统(通信设备、集成到不同系统中的电子设备、导航计算机等)相互作用。

对长气隙放电的动力学方面，特别是对先导电流的模拟，将对评估损害并最终防止这种损害有很大帮助。这是许多作品的主题(Gary er A1 1984，Gallimberti 1979，Ortega 1992，Klewe a/1974)。

最有用的描述领导者发展的模型要么基于局部热力学平衡的存在，要么基于非平衡情况的存在。第一个假设是许多争论的主题(Les Renardkes group 1977，Gary er，a/1984，Klewe et a/1974)。我们下面开展的工作涉及到第二种情况。

在这篇文章中，我们提出了一个领先者的等效电路模型，使得人们可以得到它的时空演化。这样的模型使用了物理定律和气体放电理论。此外，它比纯粹的经验模型更简单，后者使用特殊的特定条件，或者使用物理条件，后者通常非常复杂。将该等效电路模型应用于点-面间隙。假设引线是一根长圆柱形的导体。它将由单根导线的RC单元(R和C分别为电阻和电容)表示。我们在模型中使用的R值和C值是从其他研究人员对正引线(电压、电流、电荷、条纹照片)的实验结果得出的典型值。对于给定的电压形状，特别是振荡脉冲电压，我们进一步用我们的模型确定了电流和电荷。然后将结果与实验结果进行比较(Ortega ETA[1991，Ortega 1992)

2. 先导的时空发展

作为起点，我们假设引线可以用一个如图1所示的等效网络来表示。$R_0$是平面电极电阻，其典型值在100-200Ω范围内(Johannet 1987，Ratnamahilan and Hook 1993)。在这项工作中，$R_0$的值被设置为100Ω。$C_0$可以使用球面近似(假设两个电极分别是半径为$R_p$和$R_P+D$的同心球体；D为间隙长度，$R_p=2 mm$为电极半径)，并考虑其值等于球面容量的一半：

\[C _ { 0 } = 2 \pi \varepsilon _ { 0 } \frac { ( D + R _ { \rho } ) R _ { p } } { D } \tag{1}\]

当引线传播时，这对应于开关$S_i$(与脉冲发生器$G_i$相关联的接触器)闭合，并且启动的电势波将如图2所示。因此，流经线路的电流由下式给出

\[I _ { i } ( t ) = C _ { i } ( x ) \frac { d V _ { i } ( t ) } { d t } \tag{2}\] \[I _ { i } ( t ) = \frac { V _ { i } ( t ) - V _ { i - 1 } ( t ) } { R _ { i } ( x ) } \tag{3}\]

X是先导通道的轴向长度。

\[C _ { i - 1 } ( x ) \frac { d V _ { i - 1 } ( t ) } { d t } = I _ { i - 1 } ( t ) - I _ { i } ( t ) \tag{4}\]

通过将方程(2)和(3)代入方程(4) ，得到电压，然后得到先导电流

\[I ( t ) = \frac { U ( t ) - V _ { 0 } ( t ) } { R _ { 0 } } \tag{5}\]

$V_0(t)$是$C_0$电容电压。

注入间隙的空间电荷可通过将电流积分计算为

\[q ( t ) = \int _ { 0 } ^ { t } I ( t ) d t \tag{6}\]

图3为一般图表，显示积分器装置与图1所示先导器的等效电路的连接

\[V ( t ) = \frac { k R _ { 0 } } { C } \int _ { 0 } ^ { t } I ( t ) d t \tag{7}\]

k是跨导。

已经知道，电流和先导的电荷取决于施加在电极间隙的电压。在下面，我们考虑一个类似 ortega et a1(1991)和 ortega (1992)所使用的脉冲电压，以便将我们的结果与这些作者所获得的结果进行比较。这种形式的电压由阻尼振荡在双指数脉冲上的叠加构成。用3mv，48.6 kj Marx发生器产生双指数脉冲，即在不同峰值电压下的正切换脉冲。双指数电压的表达式可以通过单级脉冲发生器电路获得。这包括一个电容器 C，它被充电到所需的电压，并通过一个电路放电，其常数可以调整，以便给出所需形状的冲击电压。单级发电机的基本电路如图4所示。元素 $R_c$ 和 $C_c$，控制前面的$R_g$ 和 $C_g$，冲击电压的尾部。对电路的分析，如图4所示，允许我们得到输出电压 $u_c(t)$的表达式。通过使用拉普拉斯变换属性，我们已经

\[\frac { U _ { 0 } } { p } = I _ { 1 } R _ { g } + ( I _ { 1 } + I _ { 2 } ) \frac { 1 } { p C _ { g } } \tag{8}\]

按照理解，公式（8）的右面应该是指的开关断口两端的电压，此处的$p = jw$，整个公式（8）没看明白

\[I _ { 1 } R _ { g } = I _ { 2 } ( R _ { c } + \frac { 1 } { p C _ { c } } ) \tag{9}\] \[U _ { c } ( p ) = I _ { 2 } / ( p C _ { c } ) \tag{10}\]

将方程(8)和(9)代入(10) ，重排后得到

\[U _ { c } ( p ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { 1 } { p ^ { 2 } + b p + c } \tag{11}\]

或者

\[U _ { c } ( p ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { 1 } { ( p + \frac { 1 } { T _ { a } } ) ( p + \frac { 1 } { T _ { b } } ) } \tag{12}\] \[b = \frac { 1 } { R _ { c } C _ { c } } + \frac { 1 } { R _ { g } C _ { g } } + \frac { 1 } { R _ { c } C _ { g } } \tag{13}\] \[c = \frac { 1 } { R _ { c } R _ { g } C _ { c } C _ { g } } \tag{14}\] \[T _ { a , b } = \frac { 2 } { b \pm ( b ^ { 2 } - 4 c ) ^ { 1 / 2 } } \tag{15}\]

其中$ 1/T_a $和$ 1/T_b $是方程$ p^2 + bp + c = 0$的根。

最后，通过反演方程(12)中的拉普拉斯变换，我们得到

\[U _ { c } ( t ) = \frac { U _ { 0 } } { R _ { c } C _ { c } } \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } [ \operatorname { exp } ( - \frac { t } { T _ { a } } ) - \operatorname { exp } ( - \frac { t } { T _ { b } } ) ] \tag{16}\]

因此我们看到电压 i (t)的形状取决于时间常数$ 1/T_a $和$ 1/T_b $，这些表达式在文献中已知(ilkowski 和 kosztaluk 1985)

\[T _ { a } = ( T _ { 2 } - T _ { cr } ) / 0.7 \tag{17}\] \[T _ { b } = \frac { T _ { a } } { \operatorname { exp } [ 1.35 + 1.2 \operatorname { ln } ( T _ { 2 } / T _ { cr } ) ] } \tag{18}\]

最大值$U_c(t)$将为

\[t = T _ { cr } = \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } \operatorname { ln } ( \frac { T _ { a } } { T _ { b } } ) \tag{19}\]

其中$ 1/T_a $，$ 1/T_b $，$ 1/T_2 $和$ 1/T_cr $分别是上升时间，下降时间，半值时间，峰值时间和振幅因子。

设

\[\frac { T _ { a } T _ { b } } { ( T _ { a } - T _ { b } ) R _ { c } C _ { c } } = 1 \tag{20}\]

我们可以将$ U_c (t) $写作

\[U _ { c } ( t ) = U _ { 0 } [ \operatorname { exp } ( - \frac { t } { T _ { a } } ) - \operatorname { exp } ( - \frac { t } { T _ { b } } ) ] \tag{21}\]

其中

\[C _ { c } = \frac { T _ { a } T _ { b } } { T _ { a } - T _ { b } } \frac { 1 } { R _ { c } } \tag{22}\]

选择脉冲发生器的组成元素，使得$R_g$和$C_g$分别比$R_c$和$C_c$大。

通过方程式(15)的检验，我们得到了

\[T _ { a } \approx R _ { c } ( C _ { g } + C _ { c } ) \tag{23}\] \[T _ { b } \approx R _ { g } \frac { C _ { g } C _ { c } } { C _ { g } + C _ { c } } \tag{24}\]

这些方程可以让我们推导出$R_g$和$C_g$。另一方面，取$\delta = T_a / T_b$，我们可以推导出$U_0$(aguet and ianoz 1987)

\[U _ { 0 } = \frac { U _ { cr } } { ( \delta ^ { 1 / ( 1 - \delta ) } - \delta ^ { \delta / ( 1 - \delta ) } ) } \tag{25}\]

最后，$U_c (t)$将如图5的框图所示给出。

为了在双指数脉冲上叠加电压振荡，在电容分压器和高压电极(ortega et al 1991，ortega 1992)之间安装了电感 l (7m h < l < 110mh)。

这个电压的形状可以通过使用图6所示的冲击等效电路的元件的模拟得到，其中L将振荡的频率增加1/T。

从上面可以看出，领导者的时空参数(电流和电荷)的知识需要$ C_i $和$ R_i$元素的知识(图1)。

1. 引言

单相接地故障的回路电路如图所示。

由于回路中的等效阻抗较大，限制了放电电流及功率，单相接地故障放电的本质上是辉光放电。

放电电压、电流波形如图2所示。

电阻变化波形，零休处的电阻应较大，还未修正的图如图3所示。

研究土壤接地故障辉光放电，其与高压电气产生的故障电弧，带火花效应的接地极冲击电弧不同之处主要有以下几点：

1. 此放电持续时间长，一个完整的放电周期是工频的半个周波，即包括零休时间是10ms，如果去掉零休时间也达到6~7ms。
2. 在放电的过程中，电压和电流不断的发生变化，即引起辉光放电的场强经历从小变大又从大变小的过程。
3. 接地介质为土壤，土壤是一种导体，但导电性并没有导体那么强，这导致了其有一定的散流电阻，在散流过程中的发热导致其发生热电离，即先导放电，接地点电压越高，先导放电效应越强烈，会向土壤内部深入的更深。
4. 又由于土壤本身的导电性，包裹等离子体的未充分电离的土壤能够导电，这使得电场分布与空气放电不同，没有绝对意义上的地，这种先导放电即不能同空气放电一样发展下去，也不会发生主放电。
5. 先导放电所形成的等离子体通道，相当于向土壤内部插入一根金属导体，这使得从接地点位置看进去的接地电阻变小了，先导放电形成的等离子体通道在电压最大时刻附近最深，等效电阻最小，而此电阻由于串联在电力系统的零序回路中，会反过来影响接地点的电压，其本质上是一种场路的耦合系统。

所以，配电网发生单相土壤弧光接地故障的整个过程可以描述如下：

单相接地故障的辉光放电主要分为2个阶段，第一阶段是初次接地放电，第二阶段是初次放电电弧熄灭后的放电过程

第一阶段，当配电网架空线或电缆中的一相落到土地表面，此时会在导线和土壤的接触点的位置施加一个电压，这在土壤内部产生了电场，当电场强度达到足够高时，此时的土壤是一种导体，所以场强并不需要很高即可开始放电。土壤作为一种空气，固体和液体的混合介质，其中电场主要集中在空气两端，空气首先被电离，产生流注并迅速发展放热，从而发生先导放电，又由于前面所述原因，该放电并不会发展为主放电，所以维持在先导发展阶段，先导放电产生的等离子体通道向土壤内部延申，其延申长度与接地点施加的初始电压以及后续电压变化相关。当在第一阶段中接地电压逐步降低，由于土壤内的散热特性，使得电场已经维持先导放电所需的热量，电弧熄灭。而此时土壤性质被高温所改变，接地点连接着一种电的绝缘体。

第二阶段，由于土壤性质将接地点所接触的土壤变成了绝缘体，所以当电压再次反向升高时，土壤不会第一时间被击穿，而是当电压升高到一定程度，场强大于此介质的击穿电压时，介质被击穿，重复先导放电，随着电压抬升，先导放电强度增强，而当电压越高最大值逐渐变小时，先导放电逐步减弱，在增强和减弱的过程中，引起土壤等效散流电阻的变化。

由于土壤辉光放电的过程持续时间长，土壤辉光放电过程中，其流注发展的时间很短，这与一个完整的放电过程7~8ms相比，是一个极短的过程，几乎可以忽略，所以，研究土壤弧光接地故障的目的是研究土壤接地电阻如何变化，可以通过研究先导放电的发展着手。

首先，研究电力系统中的单相接地故障，参与电力系统电磁暂态仿真，所以建立一个描述土壤电弧发展的等效回路则很重要，目前所提出的等效回路仅考虑接地点的外特性，并未对土壤电弧发展的机理进行等效描述。

其次，土壤内发生的先导放电，由于先导通道周围的土壤为土壤，是电的导体，所以其机理与长间隙空气先导发展机理有所不同，并不能直接应用。

2. 模型

2.1 等效电路

首先，可以做一个近似假设，假设接地导线为电极，大地的绝对零点位处为另一电极，两电极是同心球体，其半径分别为$R_p$和$R_p + D$；D是间隙长度，$R_p$为电极半径，考虑其等于球形电容的一半。

\[C _ { 0 } = 2 \pi \varepsilon _ { o } \frac { ( D + R _ { p } ) R _ { p } } { D } \tag{1}\]

先导放电向土壤内发展为一圆柱体，其可以利用近似的传输线等效网络进行近似模拟。

将先导的发展过程离散化，先导通道向前发展一段，则等效网络向前扩充一个类似$\Pi$型的等效电路，而所需要确定的是每一段网络中的阻抗和导纳的参数。

当先导发展时，在最后一个网络中可推出如下公式

\[L _ { i } \frac { d i _ { i } ( t ) } { d t } = V _ { i - 1 } ( t ) - V _ { i } ( t ) - R _ { i } \dot { \imath } _ { i } ( t ) \tag{2}\] \[i _ { i } ( t ) = C _ { i } ( x ) \frac { d V _ { i } ( t ) } { d t } + G_i(x)V _ { i } ( t ) \tag{3}\] \[i _ { i - 1 } ( t ) - i _ { i } ( t ) = C _ { i - 1 } ( x ) \frac { d V _ { i - 1 } ( t ) } { d t } + G_{i-1}(x)V _ { i -1 } ( t )\tag{4}\]

为建立等效模型，列写出其状态方程。

\[\frac { d X ( t ) } { d t } = A X ( t ) + B U ( t ) \tag{5}\] \[Y ( t ) = C X ( t ) + D U ( t ) \tag{6}\]

其中A、B、C、D分别为系统动力学、控制、观测和直接传输的状态矩阵。$U(t)$和$Y (t)$分别为输入矩阵和输出矩阵。一旦状态向量X被确定，状态矩阵(A, B, C, D)就可以被计算出来，从而获得等效电路拓扑和电路参数。

先导通道刚刚建立时，先导电流为

\[i ( t ) = \frac { V _ { 0 } ( t ) - U ( t ) } { R _ { 0 } } \tag{7}\]

$V_0(t)$和$U_c(t)$分别为$C_0$电容电压和施加到间隙的电压。

2.2 能量输入

注入到先导通道的空间电荷等于基本电荷之和

\[Q ( t ) = \sum _ { 1 } ^ { n } q _ { i } = \sum _ { 0 } ^ { t } C _ { i } V _ { i } ( t ) \tag{8}\]

$V_i(t)$为$C_i$电容电压，n为前导步数。

在先导的发展过程中，总能量$W_t$以不同的形式消耗：热能、电离、辐射等。$W_t$的一部分（动能）将转移到先导通道，使其延长距离$dl_j$。 称 $W_c$ 为动能，记做

\[W_c = \beta W_t \tag{9}\]

β 是先导位移所需能量占全部能量的系数。 0 < β ≤ 1 。

在单位时间$dt$内，由于通道发展增加的土壤密度 $ρ$和体积增量 ($\pi r _ { j } ^ { 2 } d l _ { j }$) 的乘积就是增加的等离子体的质量：$m = \rho \pi r _ { j } ^ { 2 } d l _ { j }$（其中$r_j$是分支 j 的半径，气体放电最开始会形成很多枝杈，土壤放电我想先把它简化看成只有1条分支，即j=1）

设通道的半径$r_j$和温度 T 是常数：$r_j = r_0$ 和 $T = T_0$

\[W _ { c } = \frac { 1 } { 2 } \rho \pi r _ { j } ^ { 2 } d l _ { j } v _ { j } ^ { 2 } \tag{10}\]

其中 $v_j$是分支 j 的速度。可以将整个等离子体通道从上到下的发展分成若干个区域，因为每个区域的压力不同，所以质量也不同进行迭代。其中第n次迭代符合

\[\sum _ { j = 1 } ^ { n } \frac { 1 } { 2 } ( \rho \pi r _ { j } ^ { 2 } d l _ { j } ) v _ { j } ^ { 2 } = \beta \sum _ { j = 1 } ^ { n } q _ { j } E _ { j } d l _ { j } \tag{11}\]

其中 $q_j$和 $E_j$ 分别是分支 j 的电荷和电场。 因此，先导通道的每个位移$dl_j$对应的速度为

\[v _ { j } ^ { 2 } = \frac { 2 \beta } { \pi r _ { j } ^ { 2 } \rho } ( \int i _ { j } d t ) E _ { j } \tag{12}\]

如果按照仅有一条支路，那么去掉公式（11）中的求和操作，可得新的公式（12）

\[v ^ { 2 } = \frac { 2 \beta } { \pi r ^ { 2 } \rho } E I \Delta t \tag{12}\]

其中，$q = i * t$

土壤的密度一般取2.65g/cm^3。

由此可计算每一步的$\Delta l$的变化，所有的$\Delta l$加在一起，可以求得总的先导放电长度，应该是小于15cm的，再通过其他周波进行横向的验证比对，看一看能否把参数求得一个规律值。

2.3 先导发展的平均速度

在文献中描述先导放电电流由许多离散脉冲构成。

令$t_j$ 为脉冲时间$t_{pj}$与停顿时间$t_{0j}$到下一个脉冲的时间之和所对应的时间，即

\[t _ { j } = t _ { p j } + t _ { 0 j } \tag{13}\]

和$v_{pj}$和 $v_{0j}$，分别是$t_{pj}$和$t_{0j}$期间的速度。 设 $v_{al}$ 是先导放电发展的平均速度。

\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( v _ { p j } t _ { p j } + v _ { 0 j } t _ { 0 j } ) \tag{14}\]

根据公式（12）

\[v _ { p j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { p j } E _ { j } \tag{15}\] \[v _ { 0 j } ^ { 2 } = \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } q _ { 0 j } E _ { j } \tag{16}\]

将（15）和（16）代入（14）中，得到

\[v _ { a l } = \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } [ ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ] \tag{17}\]

$v_{0j}$通常相对于$v_{pj}$可以忽略不计。 $v _ { 0 j }$是在时间$t_{0}$期间先导发展的平均速度。

假设 $r_j$, β, ρ 和 $E_j$ 在整个传播过程中保持不变，发展的平均速度可写作

\[v _ { a l } = ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } + q _ { 0 j } ^ { 1 / 2 } t _ { 0 j } ) ) \tag{18}\]

当忽略$v_{0j}$时，有

\[v _ { a l } \cong ( \frac { 2 } { \pi r _ { j } ^ { 2 } } \frac { \beta } { \rho } E _ { j } ) ^ { 1 / 2 } ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{19}\]

$E_j$和/或 $q_{pj}$ 越高，先导发展的平均速度就越高。

2.4 等离子体的密度

在高温下，所有气体都可以被认为是完美的。由于先导是高度电离的土壤等离子体 (T ≥ 1000 K) ，还不确定是否可以如此应用气体定律，如果按照完美的气体定律有

\[p V = \frac { m } { M } R T \tag{20}\]

其中 p、V、m、R、T 和 M 分别是压力、体积、通道质量、理想气体常数、温度和通道的摩尔质量。

由于密度 ρ 等于 m/V，可以得到

\[\rho = \frac { M } { R } \frac { p } { T } \tag{21}\]

因此式（21）可以写为

\[\rho ( kg m ^ { - 3 } ) = \frac { k } { T ( K ) R } \tag{22}\]

其中，$k = Mp$

土壤由于深度不同，由于重力的影响，此时压力是变化的，但由于深入土壤的先导通道仅15cm，则认为土壤密度ρ 为常量。

$p = ρ \pi r^2l$

其中，$r$为先导通道半径，$l$为先导通道的深度。

2.5 先导发展头部电场计算

对每一步先导发展来说，场强 $E_j$ 是必不可少的。该场强$E_j$ 与沿通道分布的总电荷有关。 Szpor (1971) 提出了这一假设，可以使用双曲线近似来估计：

\[E _ { j } = \frac { 2 U _ { j } } { R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } \tag{23}\]

$L_z$和 D 分别是前导轴向长度和间隙长度，$U_j = U − \Delta U_j$是先导尖端上的电压（其中 U 是电极上施加的电压，$\Delta U_j$是沿通道的电压降）和 $R_e$ 等效电极的半径。

$R_e$ 可以表示为等离子长度的线性关系

\[R _ { e } = \alpha L_z \tag{24}\]

按照试验后的土壤挖掘结果，$\alpha \cong 1/10$

2.6 先导放电的平均速度计算

联立式 (19)、(22) 和 (23)

\[v _ { a l } = ( \frac { 4 \beta T _ { 0 } U _ { j } R } { \pi r _ { 0 } ^ { 2 } k R _ { e } \operatorname { ln } [ 4 ( \frac { D - L _ { z } } { R _ { e } } ) ] } ) ^ { 1 / 2 } \times ( \frac { 1 } { \sum _ { j = 1 } ^ { n } t _ { j } } \sum _ { j = 1 } ^ { n } ( q _ { p j } ^ { 1 / 2 } t _ { p j } ) ) \tag{25}\]

先导的速度取决于先导尖端 $U_j$ 处的电压、其轴向长度 $L_z$ 和其他物理参数， 还有参数$\beta$。

3. 等效电路参数

一共有4个参数，分别为电阻，电感，电纳和电导。

3.1 电阻

电阻表征的是先导通道中的电阻，其处于等离子态，其电阻值相当小，再考虑到包裹等离子的土壤为导体，其电阻远大于等离子体内的电阻，故忽略掉。

3.2 电感

电感参考空气先导放电的计算方法，主要分为2部分，一是储存在通道内的电磁能量产生的电感$L1$，二是通过先导通道的电流产生的电感$L2$。

3.2.1 储存在通道内的电磁能量产生的电感

如图所示，假设一个长度为h的通道段，流过这段通道的电流为$I$。

距离$r \leq a$处的磁场相对于通道轴为

\[B ( r ) = \frac { \mu _ { 0 } } { 2 \pi r } \frac { I \pi r ^ { 2 } } { \pi a ^ { 2 } } = \frac { \mu _ { 0 } r } { 2 \pi a ^ { 2 } } I \tag{26}\]

所储存的电磁能的密度为

\[\delta \omega ( r ) = \frac { 1 } { 2 \mu _ { 0 } } B ^ { 2 } ( r ) \tag{27}\]

或者

\[\delta \omega ( r ) = \frac { \mu _ { 0 } } { 8 \pi ^ { 2 } } I ^ { 2 } \frac { r ^ { 2 } } { a ^ { 4 } } \tag{28}\]

假设恒流I，段通道中存储的总电磁能量为

\[W = 2 \pi h \int _ { 0 } ^ { a } \delta \omega ( r ) r d r \tag{29}\]

由于

\[W = \frac { \mu _ { 0 } } { 16 \pi } I ^ { 2 } h \tag{30}\]

另一方面，这种能量也可以表示为

\[W = \frac { 1 } { 2 } L _ { 1 } I ^ { 2 } \tag{31}\]

由式(30)和式(31)可以推导出L1

\[L _ { 1 } = \frac { I } { 4 } \frac { \mu _ { 0 } } { 2 \pi } h \tag{32}\]

3.2.2 先导通道内的电流产生的电感

设$D_f$是距离导线的距离，在这一点上电场被认为是零。考虑图中所示的通道前一段的纵向部分。距离$r (a < r < D_f)$处的磁场定义为

\[B ( r ) = \frac { \mu _ { 0 } I } { 2 \pi r } \tag{33}\]

则根据(28)，所储存的电磁能的密度为

\[\delta \omega ( r ) = \frac { 1 } { 2 \mu _ { 0 } } \frac { \mu _ { 0 } ^ { 2 } I ^ { 2 } } { 4 \pi ^ { 2 } r ^ { 2 } } = \frac { \mu _ { 0 } I ^ { 2 } } { 8 \pi ^ { 2 } r ^ { 2 } } \tag{34}\]

考虑$I$为常数，总存储电磁能为式(32)

\[W = \frac { 2 \pi h \mu _ { 0 } I ^ { 2 } } { 8 \pi ^ { 2 } } \int _ { a } ^ { D f } \frac { d r } { r } = \frac { h \mu _ { 0 } I ^ { 2 } } { 4 \pi } \operatorname { ln } [ \frac { D f } { a } ] \tag{35}\]

另一方面，这种能量可以表示为

\[W = \frac { 1 } { 2 } L _ { 2 } I ^ { 2 } \tag{36}\]

因此，由式(35)和式(36)

\[L _ { 2 } = \frac { \mu _ { 0 } h } { 2 \pi } \operatorname { ln } [ \frac { D f } { a } ] \tag{37}\]

根据(32)和(37)，整个系统的电感为

\[L = \frac { \mu _ { 0 } h } { 2 \pi } [ \frac { 1 } { 4 } + \operatorname { ln } ( \frac { D f } { a } ) ] \tag{38}\]

所以，通道的单位长度电感$L_u(H/m)$是

\[L _ { u } = \frac { \mu _ { 0 } } { 2 \pi } [ 0.25 + \operatorname { ln } ( \frac { D f } { a } ) ] \tag{39}\]

3.3 电纳即对地电容

由于先导通道特别短，且直接在土壤里面，虽然理论上会存在相对绝对零点位地的电容，但特别小，此处忽略掉。

3.4 电导

电导的计算是该模型中最重要的部分，因为整个等效电路，其端口参数主要表征的为此电导参数。

如果说ab为先导通道，m为绝对0电位点，周围的土壤电阻率为$\rho$，则m点处的电阻为$\rho r / 4 \pi r^2$，即土壤电阻率乘以到m点的距离并除以r为半径的球体表面积。则m处的电位为

\[\psi ( m ) = \frac { \rho } { 4 \pi } \int _ { a } ^ { b } \frac { I ( p ) } { r ( p , m ) } d l \tag{40}\]

将先导通道分为n个$\Delta l$长度的单元，单元（j-1，j）内的散流电流$I$近似为线性分布，即

\[I ( z ) = I_{j-1} + ( z - ( j - 1 ) \Delta l ) ( I_j - I_ { j- 1 } ) / \Delta l \tag{41}\]

其中，$( j - 1 ) \Delta l < z < j \Delta l$

设每段先导通道半径为R，电流沿先导通道表面均匀分布，则相应单元表面上的流散电流密度为

\[\sigma ( x , y , z ) = ( I_{ j - 1 } - I _ { j } ) / \pi R ^ { 2 } \Delta l \tag{42}\]

在土壤中任意点$m ( x _ { m } , y _ { m } , z _ { m } )$处产生的点位为

\[u_{ab}(x_m,y_m,z_m) = \frac { \rho } { 4 \pi } \sum _ { j = 1 } ^ { n } (\int _ { (j-1)\Delta t } ^ { j \Delta t} \int _ { 0 } ^ { 2 \pi }\int _ { 0 } ^ { R } \frac { I_{j-1} - I_j } { \pi R^2 \Delta l S} \times rdrd\theta dz + \int _ { (j-1)\Delta t } ^ { j \Delta t} \int _ { 0 } ^ { 2 \pi }\int _ { 0 } ^ { R } \frac { ( I_{j-1} - I_j) rdrd\theta dz } { \pi R^2 \Delta l S }),j = 0,1,2,...n \tag{43}\] \[S = \sqrt { ( x - x _ { m } ) ^ { 2 } + ( y - y _ { m } ) ^ { 2 } + ( z - z _ { m } ) ^ { 2 } } \tag{44}\]

各节点上的电位方程组成的方程组形式为$A I = U$

解方程组求得各节点电流值，即可计算接地网流出的电流大小，并算出该接地网的接地电阻值$R = U/I$

4 计算过程

一个周波的电阻变化曲线如图所示

将先导放电发展过程提取出来，从192点到563点。

电导最大值为0.0044S，电导最小值为$2.021*10^{-4}S$，对应电阻5000Ω。

可以假定接地电阻最小值为55Ω，即先导发展最长位置的接地电阻。

4.1 计算191~192点

首先，假设在接地电阻为5kΩ时，未发生散流，所有能量均变为流注通道，按照此时的能量估算等离子体通道发展所需能量。

另一个假设，就是先导通道的单位长度对应的散流电导是固定的，即先导通道长度与散流电导是线性的关系。

\[\Delta G = \Delta l * \alpha = (G_{max} - G_{min}) / 20000\]

这里人为定义一个单位长度的分辨率，将整个发展过程分为20000份。

那么$G_{min}$位置对应的电导即先导通道的初始电导，认为此时的先导长度完全由注入能量说转化，没有散流到土壤当中。

那么$P1 = U_{start} ^2 * G_{min} * \Delta t$

求得P1 = 0.0102（J）

对应初始时刻的先导长度，$l_{start} = G_{min} / \Delta G = 0.6830cm$

4.2 计算192~193点

$W193 = U_{193} ^2 * G_{193} * \Delta t = 0.0103（J）$

其中先导发展的长度为

$l_{193} = 0.0099cm$

先导发展这些距离所需能量为$W193t = l{193} / l_{start} * 0.0102 = 1.4784*10^{-4}（J）$

$\beta = W193_t / W193 = 0.0144$

4.3 计算散流能力

再做假设，单位长度先导通道的散流能力(包括电流及热辐射等能量形式)是固定的，随着注入电流的增加，其原本长度的先导通道的散流能力固定。

计算到193点时，总的先导长度为0.6929cm，192点之前的能量全部用来形成先导通道，而在在192~193点间隔期间的能量为新增能量，其中一部分通过之前的先导通道散流出去，另外散流不出去的能量需要增长先导通道长度。

增长先导通道长度所需能量为$W193t = l{193} / l_{start} * 0.0102 = 1.4784*10^{-4}（J）$

那么剩余能量为$W193 - W193t = 0.101（J）$

即可以认为0.6929cm的先导通道，单位时间内其散流能力为0.101（J）

4.4 正向计算

按照以上数据进行正向计算。电压电流使用注入电压电流，利用前3章所述公式进行计算，并用4.1~4.3所分析的数据进行验证。其中每一个点为单位时间10us内的能量。

其发展趋势能够保持一致，下一步需要继续确定土壤参数。

5 过程记录

figure(7) plot(W_t_Ej*4.15) hold on; plot(W_delta) title(‘土壤散流能量曲线’) xlabel(‘点数（100000Hz）’) ylabel(‘散流能量（J）’) legend(‘计算’,’实际’)

注意乘以了一个4.5后，结论很曲线很吻合。

寻找为什么会出现这个系数

是由于先导发展的头部电场计算值所引起的。

那么如何合理确定先导发展头部的电势呢？还是可以通过电导的计算而求得。