Zamanan N, Sykulski J. The evolution of high impedance fault modeling[C]//2014 16th International Conference on Harmonics and Quality of Power (ICHQP). IEEE, 2014: 77-81.

高阻接地故障模型的进化

The Evolution of High Impedance Fault Modeling

摘要

越来越需要更加详细，准确的建模技术来预测电力系统的瞬态响应，尤其是由高阻抗电弧故障（HIF）引起的瞬态响应。在设计和开发改进的设备和新的保护技术方面尤其如此。准确预测故障瞬变需要系统中所有组件的详细和全面表示，而瞬变研究则需要在远高于正常电源频率的频率范围内进行。HIF是一个非常复杂的现象，并表现出高度非线性的行为。最鲜明的特征是非线性和不对称性。非线性是由于HIF的电压-电流特性曲线本身是非线性的这一事实引起的。还可以观察到，故障电流在正负半个周期内具有不同的波形，这称为不对称。HIF之后的每个循环中都存在非线性和不对称性。为了获得HIF的良好表示，必须开发一个模型，该模型具有上述特征以及HIF的谐波含量。本文介绍了一种新的HIF模型，它还回顾并总结了一些用于建模高阻抗故障的方法及其发展趋势。

1. 引言

配电馈线上的高阻抗故障（HIF）是一种异常电路状况，会导致能量以不同于预期负载的方式耗散。大多数故障可以被及时检测和隔离，但是在实践中仍然很难检测到高阻抗故障和电弧故障[2]，因为故障产生的电流很小并且模仿正常负载。配电馈线导体易于与邻近物体发生物理接触，例如杂草丛生的植物，建筑物墙壁，沥青，高阻抗物体或表面，这限制了配电系统故障的电流值并阻止了常规的过电流保护装置的运行。在电弧放电HIF的情况下，当通电的导体接触地面时，电触点将不牢固。由于在地面和导体之间存在空气，所以在这么短的距离内高电位差会激发电弧的出现。高阻抗故障（HIF）在其瞬态和稳态状态下具有可识别的特征。它们还会导致电弧放电，这是由于与地面或接地物体接触不良而导致气隙的结果。当导体破裂并掉落在不导电的表面（例如柏油路，沙子，水泥，草或树枝）时，就会发生这种情况，几乎不会产生任何可测量的电流。 HIF经常引起的电弧放电会导致致命的火灾和触电死亡。 HIF可能会导致电气系统损坏，客户断电，公共危险或由于电弧和闪光以及可能发生的财产火灾而导致的不安全状况。

HIF的精确建模方法对于开发可靠的检测算法至关重要。 HIF模型的数据应包含HIF的复杂特征，例如非线性，不对称性和电弧故障典型的低频现象。已经提出了一些HIF的建模方法[1-4]。尽管所有这些方法都很好地表示了HIF的非线性行为，但考虑其他特性时仍会遇到困难。

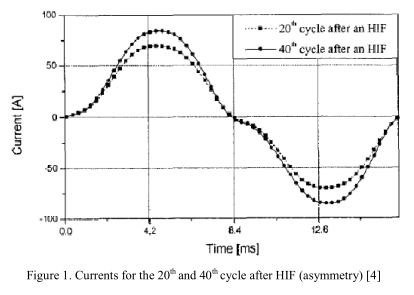
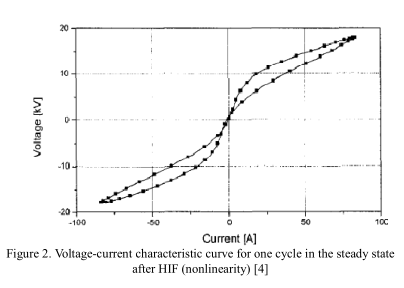
根据韩国电力公司（KEPCO）的实验工作[4]，HIF实验数据是在22.9kV配电系统上收集的。实验总数为32，采样频率为10 kHz。图1例示了发生HIF后第20和第40个周期的电流。两种电流都表现出一定的不对称性。图2显示了电压-电流曲线，并显示了非线性程度。我们可以看到，HIF的电流曲线和电流电压曲线的“签名”具有非常独特的形状。在设计HIF模型时，必须考虑到所开发的模型应具有HIF的上述特性和谐波含量。

2. 高阻模型回顾

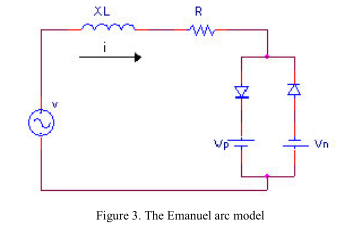
与HIF关联的电弧会以热量的形式耗散能量，从而将土壤中的水分转变成蒸汽，并将草燃烧成烟。在与电力线下降相关的电弧现象中，由于在地面和导体之间存在空气，所以在如此短的距离内的高电势差会激发电弧的出现。而且，这些故障经常伴有电弧放电，从而构成火灾隐患。因此，从公共安全和运行可靠性的角度来看，HIF的检测至关重要。高阻抗故障很难建模，因为大多数HIF现象都涉及电弧放电，到目前为止，尚未完美建模。先前的一些研究人员已经达成共识，即HIF是非线性且不对称的，并且建模应包括随机和动态电弧质量。伊曼纽尔模型基于实验室测量和理论成分[1]，建议两个直流源反并联连接两个二极管，以模拟零周期的电弧和不对称性，如图3所示。

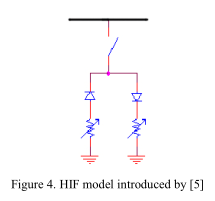
在[5]中，考虑到接地阻抗的非线性，将电弧高阻抗故障建模为两组二极管（正负），分别与电阻和直流电源串联。图4说明了该模型。

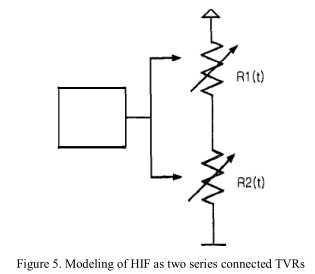
参考文献[4]提出了由EMTP中的控制系统瞬态分析（TACS）控制的两个串联时变电阻（TVR）来建模HIF。一个TVR用于故障后稳定状态下一个周期的电压-电流特性的非线性和不对称性，然后，另一个TVR用于根据HIF之后的瞬态状态下的波形来表示累积和肩峰特性，如图5所示。

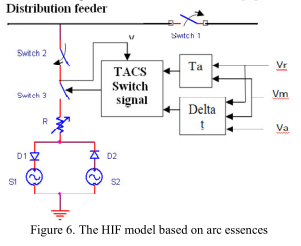
基于电弧理论，在[6]中介绍了一个包含非线性阻抗，时变电压源和控制系统（TACS），受控开关的瞬态分析的HIF逼真的模型，如图6所示。

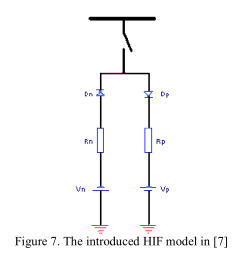
简化的Emanuel模型在[7]中引入。如图7所示，模型具有两个不相等的电阻，分别代表不对称故障电流。 Rp和Rn这两个电阻代表故障电阻：不相等的值允许模拟非对称故障电流。

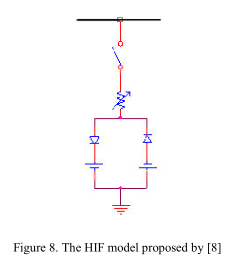
在[8]中引入了简化的2二极管HIF模型，如图8所示。该模型包括一个非线性电阻器，两个二极管和两个直流电源，每半个周期随机改变幅度。

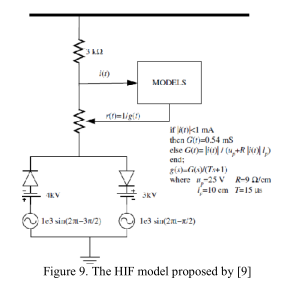
HIF模型是在[9]中引入的，如图9所示。它包含两个二极管和极化斜坡电压，以控制电弧点火瞬间。电弧模型由线性电阻器（代表接地路径电阻），非线性时变电阻器r（t）（代表动态电弧）以及直流和交流电源组成。这些源确保电弧电流和电压（直流源）以及可变的电弧着火点和熄灭点（交流源）不对称。

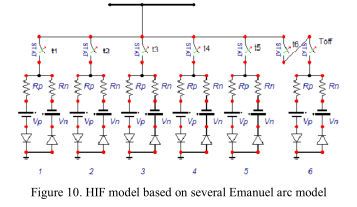
基于伊曼纽尔模型，[10]中的作者提出了一个模型，该模型使用了多个并联的电弧模型，它们的组合产生了HIF电流。图10显示了此HIF模型。使用EMTP中的STATISTIC开关显示HIF的随机状态。第六弧模型中的图10显示了打开和关闭一个弧的状态。

许多作者研究了HIF模型理论以及HIF电弧中电压和电流的动力学。大多数研究基于实验室研究。如上图所示，基于伊曼纽尔弧模型[1]引入和开发了许多模型，研究人员已尝试完成该模型并提出了一个更好的HIF模型。另外，本文还介绍了一种新的HIF模型。

3. 本文提出的HIF模型

本文提出的高阻抗故障模型如图11所示，包括两个直流电源Vp和Vn，分别代表土壤中和/或树木与配电线路之间空气的电弧电压。二极管之间的两个电阻Rp和Rn分别代表树木的电阻和/或接地电阻，并且由于大多数观察到的电弧都发生在高电感电路中[11]，因此在电路中添加了两个电感Lp和Ln。电感的影响导致V-I曲线呈非线性环路形状，并导致HIF电流达到所需的不对称形状。当线路电压大于正直流电压Vp时，故障电流开始流向地面。当线路电压小于负直流电压Vn时，故障电流从地面反向反向。在线路电压介于Vp和Vn之间的情况下，线路电压被Vp或Vn抵消，因此不会流过故障电流。典型的故障电流和V-I曲线如图12和13所示。

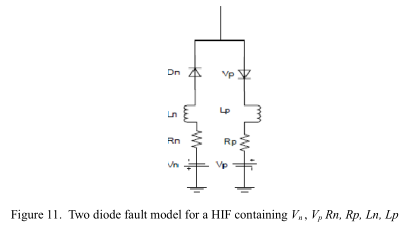
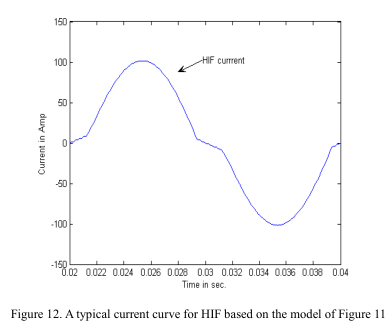
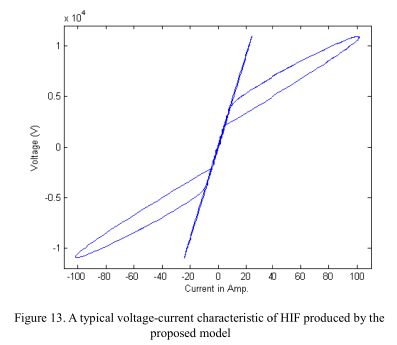
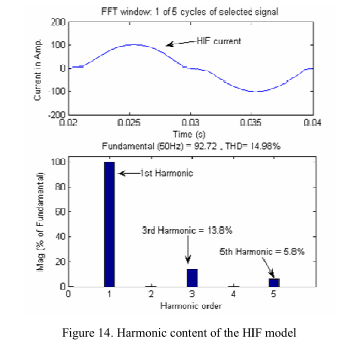
图14显示了本文提出的HIF电弧模型的电流谐波含量，相对于基波3次和5次谐波分别是13.8%和5.8%。与文献[12]中列出的KEPCO数据，仿真结果很好的进行了拟合，尤其是谐波含量方面。另一方面，提出的HIF模型可以复现文献[4]的实验结果和文献[12]的分析结果。同样重要的是，模型的可调整参数允许产生的HIF特性发生变化。

4. 结论

这篇论文的目的是开发一个模型，用来表征和预测高阻接地故障的特征，包括非线性，不对称和谐波含量。电弧发生的物理过程导致独特的信号特征。因此，提出一个新的高阻接地故障模型，并测试了模型性能，包含主动和被动元器件，电压源、二极管、电阻和电感，这个可以很好的表征电弧特性。这个模型表征了独特的高阻接地电压和电流曲线斜率，谐波特性，和实验特征。因此，可以将所提出的模型视为高阻抗故障特性的适当且物理上合理的表示，并且可以利用该模型来生成开发更可靠的HIF检测算法所需的各种数据。