接地电极土壤电离模型的严格审查（A critical review on soil ionisation modelling for grounding electrodes）

DOI 10.1515/aee-2016-0033

摘要

由于土壤电离现象，在脉冲条件下接地电极电阻会非线性变化。已经提出了几种模型来模拟用于接地电极应用的土壤电离。但是，迄今为止，还没有尝试将所有这些作品汇编成一篇全面的评论文章。因此，本文旨在总结该领域的所有相关著作，作为一站式参考。参考文献，本文旨在总结土壤电离模型的工作原理以及模型的准确性和性能分析。本文特别强调了可用模型在准确性和性能方面的不足。这些知识将有助于开发新的准确有效的土壤电离模型。

1. 简介

当高冲击电流通过接地导体[1-5]排放到土壤中时，会发生土壤击穿现象。由于土壤的破坏，土壤的电阻降低，因此接地电极的峰值电压响应降低。因此，土壤击穿提高了接地系统的效率。提出了两个主要过程来解释在高脉冲电流放电期间土壤传导的增加，即（1）热加热过程和（2）土壤电离过程。在热加热过程中，放电电流会增加土壤颗粒中现有水的填充温度。由于加热过程，热水的电阻率降低，这继而导致散装土壤的电阻率降低，从而降低了接地电极的电阻[6-8]。在土壤电离过程中，土壤颗粒之间的空隙中的电场增强，导致土壤分解[5，9-11]。由于电离空气的电阻远小于土壤颗粒的电阻，因此等效土壤电阻降低。值得注意的是，土壤电离是土壤分解现象的主要因素。

已经提出了几种电路模型来模拟土壤电离及其对接地电极电阻的影响。尽管在该领域进行了许多公开的研究，但似乎没有一份全面的评论文章可以对优缺点进行评估。参考文献，撰写本综述论文时要谨记以下目标：（1）总结CIGRE [4]，Bellaschi等人提出的可用土壤电离模型的功能和工作原理。 [3]，Nor等。 [12]和Liew和Darveniza [13]和（2）在准确性，所用方法的复杂性和应用方面评估了所述土壤电离模型的优缺点。在本文的最后，还提供了土壤电离模型与相应实验结果之间的比较。本文的其余部分安排如下：

第2节介绍了介绍土壤电离过程和接地电极电阻特性的理论背景。在第3节中，对土壤电离模型进行了严格审查。第四部分讨论了土壤电离模型的准确性和性能分析。最后，第5节给出了整体讨论和结论。

2. 理论背景

在本节中，将对土壤电离过程（最普遍的过程）进行说明。然后，介绍了从实验情况获得的冲击电流下接地电极电阻的关键特性。这些关键特性已被CIGRE [4]，Bellaschi等人用于调查提出的土壤电离模型的准确性和性能。 [3]，Nor等。 [12]和Liew和Darveniza [13]。

2.1 土壤电离过程

在土壤介质中，气穴和土壤颗粒充当混合电介质。这是因为气孔（σair和εair）和土壤颗粒（σsoil和εsoil）的电导率和介电常数不同。因此，气孔与土壤颗粒之间的界面处的位移矢量相等，即E airεair = E土壤εSoil。当电流放电到大地时，气隙和土壤颗粒的电阻路径充当电阻分压器。由于空气的介电常数远大于土壤颗粒的介电常数，因此气隙中的电场超过了击穿水平[14]。由于空气击穿，电离的空气在土壤内部形成电弧。在土壤中，电弧在电流峰值处完全发达。电弧在土壤中传导电流的体积称为电弧通道。在电流从零上升到峰值的持续时间内，电弧电阻是电流的函数；通过增加电流将减小电弧电阻。电弧电阻的最小值在电流峰值处获得[13]。对于电流在衰减时间内的持续时间，电弧的电阻主要取决于电弧通道和土壤之间的能量平衡，而不是电流幅度。通过减少存储在电弧通道中的能量，电弧的电阻会增加，直到电弧在土壤中熄灭为止。在任何情况下的土壤动态阻力都等于等效的平行土壤阻力和耐电弧性。由于电弧的电阻发生了变化，土壤动电阻在脉冲电流的持续时间内发生了变化。由于电弧通道和土壤之间的能量平衡，动态土壤阻力将显示出滞后特性[13，15]。

2.2 接地极电阻特性

在本节中，Bellaschi等人完成了一个实验案例。讨论接地电极电阻的特性。实验是在土壤中使用半径为7.9 mm的带驱动力的2.44 m长电极，电阻率为162Ω.m（Ground-M）进行的。注入电流的幅度为6.6 kA，波形为15 µs / 42 µs。通过实验设置获得的瞬态电阻为电压和电流的瞬时比率（波形图CSH-2184-CH＆CI）。

图1示出了电流和电压波形，以及电极的接地电极电阻的变化。注意，获得的电阻是电压和电流的瞬时比，即R（t）= v（t）/ i（t）。如该图所示，当冲击电流分散到地时，接地电极电阻值非线性地变化。

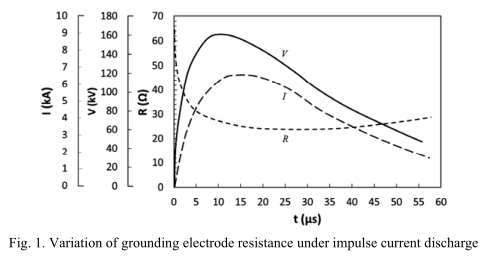
在电流从零上升到峰值的持续时间内，接地电极电阻从测得的低电流ac值（64Ω）减小到一个最小值（24.5Ω）。在电流峰值附近获得电阻的最小值。在电流从峰值减小到零的持续时间内，接地电极电阻在测得的低电流ac值中缓慢增加。这是因为存储在电弧通道中的能量不允许快速增加电阻。

如图2所示的电阻电流特性所示，电阻的缓慢增加会引起磁滞效应。

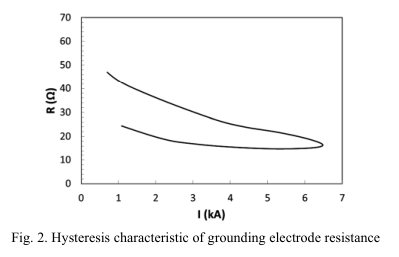
3. 土壤电离模型

在本节中，CIGRE [4]，Bellaschi等人建议的土壤电离模型的概念。 [3]，Nor等。 [12]，以及Liew和Darveniza [13]。此外，本文还重点介绍了建议模型的优缺点。

3.1 CIGRE模型

CIGRE [4]提出的模型是计算接地电极电阻随电流变化的经验公式。在该模型中，电离的开始主要取决于土壤的电阻率。土壤电离开始后，接地电极电阻随电流的对数而减小。 CIGRE模型将电离区的电阻视为零。该模型考虑了土壤电离，考虑了电离区的等效几何形状以计算接地电极电阻。简化模型考虑在高振幅电流下计算接地电极电阻以接近平方根相关电流，而在低振幅电流下计算接地电极电阻接近零。此外，该模型还可以估算低振幅电流和高振幅电流之间的对数关系。在考虑土壤电离的情况下计算接地电极电阻的建议表达式为

$R _ { i } = \frac { R } { \sqrt { 1 + i ( t ) / I _ { g } } } \tag{1}$

其中R是以[Ω]为单位的低电流接地电极电阻，而i（t）是以[kA]为单位的脉冲电流。 I g是发生土壤电离的极限电流，单位为[kA]，给出

$I _ { g } = \frac { E _ { c } \rho } { 2 \pi R ^ { 2 } } \tag{2}$

其中，ρ是土壤电阻率，单位为[Ω.m]，E c是土壤临界电场强度，单位为[kV / m]，CIGRE建议将其设为400 kV / m。然而，在许多先前的研究中已经建议将各种E c值应用于接地电极电阻计算，范围从50 kV / m [3]到1500 kV / m [16]。正如在[17]中得出的结论，当考虑到[14]中正确的E c值时，使用CIGRE模型以及电磁模型获得的结果是可比的。因此，可以说CIGRE模型计算接地电极电阻的精度取决于E c值。该模型很简单，可以轻松地用于电路方法中。但是，CIGRE模型仅对最长30 m的电极有效[4]。该模型在计算中没有考虑能量平衡的概念。因此，该模型无法显示接地电极电阻的磁滞特性。

3.2 Bellaschi 模型

Bellaschi等人提出的模型。 [3]使用基本公式来计算低电流接地电极的电阻值，该公式由Dwight [18]公式针对单驱动电极和多驱动电极提出。对于单个驱动电极，要考虑以下关系

$R = \frac { \rho } { 2 \pi l } [ 1 n ( \frac { 4 l } { a } ) - 1 ] \tag{3}$

其中ρ是土壤电阻率，单位为[Ω.m]，l是电极长度，单位为[m]，a是导体半径，单位为[m]。为了考虑土壤电离对接地电极电阻的影响，该模型将电离区的几何形状作为接地电极的新几何形状考虑在内。这是因为电弧的电阻被认为是零。在该术语中，将电离区的长度和半径用作导体有效半径ai和导体有效长度li。为了计算有效半径ai，考虑以下关系。

$a _ { i } = \frac { a i ( t ) } { I _ { c } } \tag{4}$

其中a是导体半径，单位为[m]，i（t）是脉冲电流强度，单位为[kA]，I c是临界电流，单位为[kA]，在该临界电流处，土壤电离发生在电极表面。为了确定临界电流I c，使用以下关系

$I _ { c } = \frac { 2 \pi a l E _ { c } } { \rho } \tag{5}$

需要注意的是，E c是从接地电极的实验设置中获得的，需要事先进行建模。 a i与电流的关系用于计算导体有效长度$l_i$为

$\frac { i ( t ) } { I _ { c } } = \frac { a _ { i } l _ { i } } { a l } \tag{6}$

该模型可用于多电极系统。为此，参考相关公式从（4）至（6）获得有效半径和有效长度，以计算多电极系统的电阻[18]。 Bellaschi模型很简单，适用于电路方法。但是，模型的准确性很大程度上取决于E c值。注意，该模型在换向中未考虑能量平衡概念。

3.3 Nor 模型

Nor等人提出的模型。 [12]是基于电路的模型。该电路包括代表电极的电阻和电感的串联元件R杆和L杆，以及由R 1 -C沙和R 2 -L电路组成的两个并联分支，分别代表预电离和后电离电路，如图1所示。。3.电感L确定电离所需的时间延迟。在电离分支中，电阻R 1表示由于热效应和具有土壤电容效应的土壤特性（$C_sand$）引起的土壤传导。在后电离分支中，R 2电阻表示电离完全扩展后的导电行为。应当注意，电感L的值必须通过反复试验确定。另外，Nor等人没有提出任何关系。计算$C_sand$的价值。

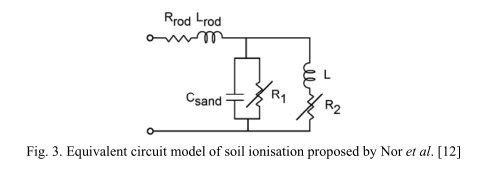
Nor等人提出的模型。是可以校准并应用于所有类型的脉冲响应和土壤样品的通用模型。前述电阻R 1和R 2具有很强的非线性电压-电流特性，需要使用曲线拟合法来确定。然而，应当注意，曲线拟合方法的应用可能固有地在确定电阻值时引起误差。电阻R 1和R 2的值作为电流的函数表示为R 1（i）和R 2（i）。在该模型中，考虑了电离时间。脉冲条件下的动态土壤阻力表示为

$R ( t ) = R _ { 1 } ( i ) \cdot ( \frac { R _ { 2 } ( i ) } { R _ { 1 } ( i ) } + e ^ { t / \tau _ { i } } ) \tag{7}$

其中τi是电离时间常数。但是，此模型未考虑去离子时间。 Nor模型也无法在脉冲电流的衰减持续时间内准确预测电阻特性。该模型仅能充分模拟具有电离前后特性的情况。该模型很简单，但是受获得电离前后分支中的电阻所需的实验数据的影响。除非使用实验数据来校准模型，否则Nor模型无法准确产生正确的接地电极电阻及其电压响应。最后，该模型没有考虑能量平衡的概念，因为模型中未考虑去离子时间。

3.4 Liew-Darveniza 模型

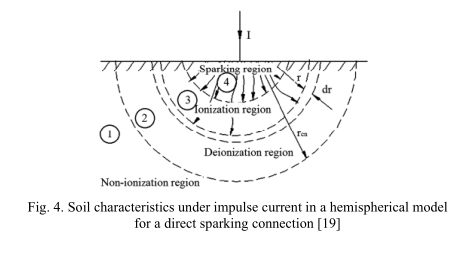
Liew和Darveniza [13]提出的动态土壤模型考虑了电离考虑的接地电极电阻建模的解析关系。该模型试图描述雷击时土壤的瞬态行为。该模型考虑了电离区的电离电阻。在此模型中，引入了三个区域，分别称为电离区域，去离子区域和非电离区域。但是，该模型无法描述电弧现象，该现象发生在从动杆附近，即土壤电阻率变为零的区域。为此，稍后在[19]中对模型进行了修改。根据改进的模型，将火花区域视为区域4，如图4所示。在该区域中，放电电流J的电流密度远高于临界值J c。在区域3中，土壤被电离，并且该电离向外解散。由于电流密度J小于临界值J c，区域2中的土壤开始恢复。最后，将未受影响的散装土壤作为区域1纳入模型。图5所示为电离土壤的电阻率曲线，以显示土壤电阻率随电流密度的变化。在电流放电的情况下，土壤电阻率为ρ0，并且如区域a所示，土壤未被电离。当电流密度达到临界电流密度J c时，土壤电离开始（区域b）。此时，土壤电阻率逐渐降低，如式（8）所示，达到ρ值。

$\rho = \rho _ { 0 } \cdot e ^ { \frac { - t } { \tau _ { 1 } } } \tag{8}$

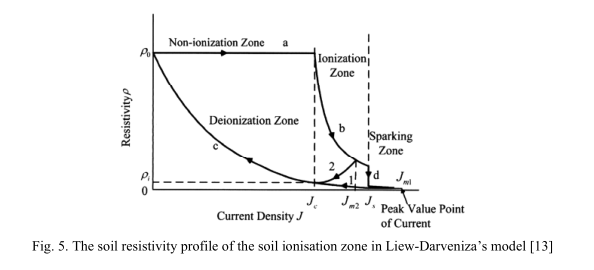
电离时间常数τ1估计为2 µs，t是从电离开始测量的时间。如果电流密度超过临界值，则跟踪将刺穿土壤（区域d）。该电流由（9）获得的J s表示。

$J _ { s } = \alpha \cdot J _ { c } \text { and } \alpha \geq 1 \tag{9}$

其中，α是系数，对于任何类型的土壤都可以确定，并且与电流幅度呈指数关系。如果不产生火花，则土壤会恢复，直到根据（10）的τ2（区域c）之后土壤电阻率ρ恢复为止。

$\rho = \rho _ { i } + ( \rho _ { 0 } - \rho _ { i } ) \cdot ( 1 - e ^ { - t / \tau _ { 2 } } ) \cdot ( 1 - J / J _ { c } ) ^ { 2 } \tag{10}$

其中，ρi是土壤电阻率的最小值，估计的恢复时间为τ2 = 4.5 µs。

由于$J_c =ρE_c$，因此临界电场$E_c$的正确值对于确定临界电流密度至关重要。因此，可以说模型的精度很大程度上取决于从实验设置中获得的临界电场值$E_c$。为了计算垂直接地电极的电阻，考虑了Liew和Darveniza提出的公式：

$R = \frac { \rho } { 2 \pi l } \operatorname { ln } \frac { a + l } { a } \tag{11}$

但是，通过Liew和Darveniza公式和Dwight公式获得的针对不同电极长度和半径的计算电阻之间的比较显示出约10％的差异[13]。 Liew-Darveniza的模型不能恰当地解释电极的电涌行为，在这种行为中，高电流会导致离散的击穿路径，而不是导致电离增加的扩散过程[13]。因此，需要更多的研究来改进模型。 Sekioka等人对该模型的解释。 [20]揭示了Liew-Darveniza的模型考虑了能量平衡的概念。该模型还显示了在脉冲条件下接地电极电阻的磁滞特性。在模型的等效电路中，电极电感和土壤电容被忽略。

当电感特性和电容特性变得很重要时，这可能会导致电极在快速和慢速前沿电流下的电压响应出现较大的误差[21]。与其他审查模型的方法相比，该模型的方法更为复杂。

4. 准确分析模型

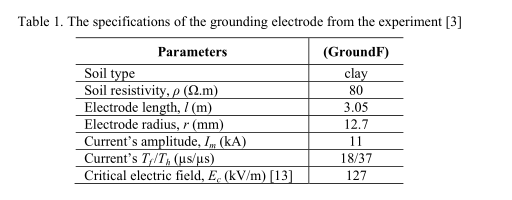
本节将在计算接地电极电阻和电压响应方面讨论上述模型的准确性。为了显示模型的准确性，将电极模型的电阻和电压响应与实验获得的结果进行了比较[3]。为此，根据Bellaschi等人的著名实验研究，确定的实验案例为Ground-F（示波图CSH-2184-CO）。 [3]被考虑在内。表1中列出了实验案例的规格。应注意，临界电场值取自[13]为127 kV / m。

从实验中获得的接地电极电阻变化和电压响应（Ground-F），以及通过CIGRE，Bellaschi，Nor和Liew-Darveniza模型获得的电压响应如图6所示。如图所示，在t = 0时，接地电极电阻的低电流值为24.4Ω，在t = 20 µs时，在10.9Ω处获得接地电极电阻的最小值。

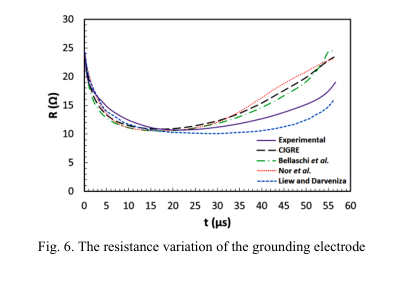
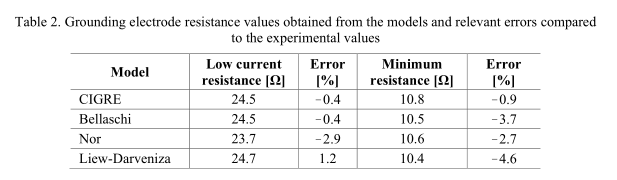
由模型计算出的电阻值示于表2中。根据表2，相对于实验电阻值而言，就针对低电流计算并满足最小值的电阻而言，模型的精度是令人满意的。但是，应注意，如实验图所示，只有Liew-Darveniza和Nor模型计算的最小电阻值约为20 µs。但是，CIGRE和Bellaschi模型在t = 18 µs时计算出接地电极电阻的最小值。从模型获得的在t = 0 – 18 µs持续时间内的电阻值与实验值相比，误差在15％以内。 t = 18 µs之后，用于计算接地电极电阻的模型的误差增加。在40％的t = 50 µs时可获得最大误差。总而言之，根据图6可以说，与实验电阻值相比，模型中的Liew-Darveniza模型在计算接地电极电阻值时的误差要低得多。

与实验值比较，由模型计算出的接地电极电阻的磁滞特性如图7所示。CIGRE，Bellaschi和Nor模型未能显示出该电阻的磁滞特性。这是因为这些模型在计算衰减时间中的电流持续时间时并未考虑能量平衡的概念。相反，Liew-Darveniza的模型显示了电阻的磁滞特性。但是，Liew-Darveniza模型显示的磁滞特性与实验结果相比有所不同。

通过模型计算并通过实验获得的电极的电压波形如图8所示。根据实验的电压峰值为120 kV。

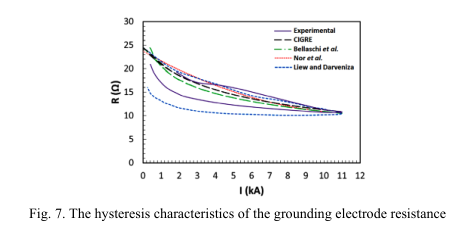
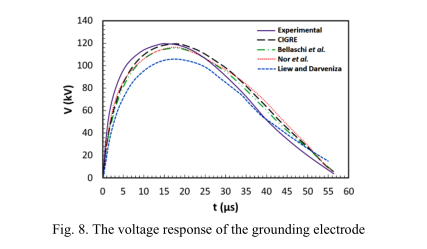
表3列出了模型计算出的值及其与实验值相比的误差。CIGRE和Nor模型计算出的电压峰值接近实验值。相反，Liew-Darveniza和Bellaschi的模型在计算电压峰值时有错误。所有模型的电压波形均与实验的电压波形不同。此外，与实验相比，由模型计算出的电压峰值更低。

5. 讨论和总结

根据评论，所有模型都需要校准实验数据，以便对接地电极进行建模。 CIGRE，Bellaschi和Liew-Darveniza模型取决于临界电场值，而Nor模型则需要电压和电流波形。应当注意，临界电场值以及电压和电流数据主要用于确定接地电极的最小电阻值。没有这些数据，所有模型都无法准确建模接地电极。所有模型都可以确定相对于电流峰值的最小接地电极电阻值。在电流处于衰减时间期间持续时间内计算接地电极电阻时，模型所产生的误差大于电流处于上升时间期间持续时间所计算出的值的误差。从简化计算的角度来看，CIGRE和Bellaschi模型比Nor和Liew-Darveniza模型具有优势。与通过Nor和Liew-Darveniza模型获得的电压峰值以及与实验值相比，通过CIGRE模型获得的电压峰值更加准确。模型也无法准确地模拟通过实验获得的电压波形。但是，没有实验数据，也无法使用Nor模型来获得电压波形。考虑到能量平衡的概念，Liew-Darveniza的模型在对接地电极电阻的特性进行建模方面更为准确。此外，在这些模型中，只有Liew-Darveniza的模型可以代表接地电极电阻的磁滞特性。

参考文献

[1] Mokhtari M., Abdul-Malek Z., Salam Z., The effect of soil ionization on transient grounding electrode resistance in non-homogeneous soil conditions, International Transactions on Electrical Energy Systems 26: 1462-1475 (2016). [2] Mokhtari M., Abdul-Malek Z., Progress Earthing Studies for Modern Life Style, Universiti Teknologi Malaysia (2015). [3] Bellaschi P.L., Armington R.E., Snowden A.E., Impulse and 60-cycle characteristics of driven grounds-II, Transactions of the American Institute of Electrical Engineers 61(6): 349 - 363 (1942). [4] CIGRE Working Group 33-01 (Lightning) of Study Committee 33, Overvoltages and insulation coordination, Guide to procedures for estimating the lightning performance of transmission lines, Paris October (1991). [5] Mousa A.M., The soil ionization gradient associated with discharge of high currents into concentrated electrodes, IEEE Transactions on Power Delivery 9(3): 1669-1677 (1994). [6] Schon J.H., Physical Properties of Rocks: Fundamentals and Principles of Petrophysics, Elsevier (1998). [7] Snowden D.P., Erler J.W., Initiation of electrical breakdown of soil by water vaporization, IEEE Transactions on Nuclear Science 30(6): 4568 - 4571 (1983). [8] Van Lint V.A.J., Erler J.W., Electric breakdown of earth in coaxial geometry, IEEE Transactions on Nuclear Science 29(6): 1891 - 1896 (1982). [9] Leadon R.E., Flanagan T.M., Mallon C.E., Denson R., Effect of ambient gas on arc initiation characteristics in soil, IEEE Transactions on Nuclear Science 30(6): 4572-6 (1983). [10] Flanagan T.M., Mallon C.E., Denson R., Smith I., Electrical breakdown characteristics of soil, IEEE Transactions on Nuclear Science 29(6): 1887-1890 (1982). [11] Flanagan T.M., Mallon C.E., Denson R., Leadon R.E., Electrical breakdown properties of soil, IEEE Transactions on Nuclear Science 28(6): 4432 - 4439 (1981). [12] Nor N.M., Haddad A., Griffiths H., Characterization of ionization phenomena in soils under fast impulses, IEEE Transactions on Power Delivery 21(1): 353-361 (2006). [13] Liew A.C., Darveniza M., Dynamic model of impulse characteristics of concentrated earths, Proceedings of the Institution of Electrical Engineers 121(2): 123-135 (1974). [14] Manna T.K., Chowdhuri P., Generalised equation of soil critical electric field E C based on impulse tests and measured soil electrical parameters, IET Generation Transmission Distribution 1(5): 811-817 (2007). [15] Kosztaluk R., Loboda M., Mukhedkar D., Experimental study of transient ground impedances, IEEE Power Engineering Review 1(11): 44-51 (1981). [16] Handbook for improving overhead transmission line lightning performance, Electrical Power Research Institution (EPRI) (2004). [17] Mokhtari M., Abdul-Malek Z., The effect of grounding electrode parameters on soil ionization and transient grounding resistance using electromagnetic field approach, Applied Mechanics and Materials 554: 628-32 (2014). [18] Dwight H.B., Calculation of resistances to ground, Electrical Engineering 55(12): 1319-1328 (1936). [19] Wang J., Liew A.C., Darveniza M., Extension of dynamic model of impulse behavior of concentrated grounds at high currents, IEEE Transactions on Power Delivery 20(3): 2160-2165 (2005). [20] Sekioka S., Lorentzou M.I., Philippakou M.P., Prousalidis J.M., Current-dependent grounding resistance model based on energy balance of soil ionization, IEEE Transactions on Power Delivery 21(1): 194-201 (2006). [21] Mokhtari M., Abdul-Malek Z., Salam Z., An improved circuit-based model of a grounding electrode by considering the current rate of rise and soil ionization factors, IEEE Transactions on Power Delivery 30(1): 211-219 (2015).