从前不懂得文献管理的重要性，但我估计大多数人和过去的我一样，作为搞科研的学生而言，最重要的文献资料是论文，从前的自己是怎样管理论文的呢，是按照课题，研究方向，具体研究内容，关键字进行文件夹分类，自己的报告放在哪个文件夹，基本上对应的文件夹里总会出现另一个文件夹叫做“资料”或“论文”。

于是在我的硬盘上出现了海量的属于不同方向的“资料”。

我觉得我有资格进行Markdown编辑软件的测评，因为我真的是大面积的使用了不同的markdown写作软件来寻找小书匠，总的来说，小书匠是一款美观度稍差，但功能性可以打的全部其他markdown写作软件满地找牙的优秀产品，其在各个维度上的完成度都堪称优秀，而且还在不断迭代增加很实用的功能。

据不完全统计：

Mac平台：

Mweb、Ulysses、Bear

Win平台：

印象笔记、为知笔记、有道云笔记、MarkdownPad、Cmd Markdown、Obsidian

跨平台：

Typora、马克飞象、飞书、语雀、Notion、小书匠

按照自己的需求，众里寻他千百度，感谢有这样一款软件。

转自了凡春秋的博客

工具箱的使用

工具箱函数

运行help index_emd可以查看工具箱提供的函数，如下

index_emd.M list of functions in the EMD package

type help function_name for more information on a specific function

Empirical Mode Decomposition

研究土壤电弧的电离过程。

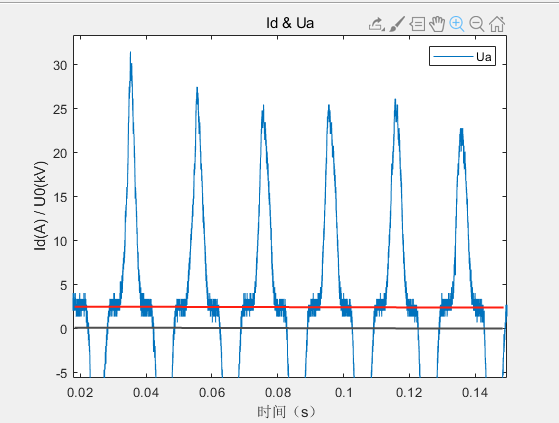
测量到的电弧电流波形会有直流分量，这个直流分量不知道是系统产生的还是罗氏线圈的零漂，鉴于罗氏线圈是无法测量直流分量的，那么大概率应该是干扰导致的零漂，在分析电弧的电离区域时，需要首先把直流分量去掉。

去掉直流分量并不难，传统经验是用FFT分析波形，将直流量提取出来即可。但电弧是按照半周波为单位完成一次击穿燃弧到熄弧的过程的，所以按照每个周期为单位对直流分量进行识别处理。

土壤冲激特性的动力学模型

Dynamic model of impulse characteristics of concentrated earths

ps：所有的从动杆或驱动杆的意思都是接地极

摘要

建立了描述多个集中土非线性电涌电流特性的动力学模型。 该模型在电阻率范围从5000 Ω cm到31000 Ω cm的土壤中，不时准确地解释了这些地球的浪涌行为。 与以前描述它们的方法相比，这带来了显着的改进。 使用新模型研究高雷电流下的集中地时，可以预料到比以前假设更大的电涌减小因子。 这项研究旨在克服以前从微不足道的实验结果中推断出值的困难。

摘要

由于土壤离子化，在高脉冲电流下接地电极的有效半径变得大于电极的外径。 因此，接地脉冲阻抗不同于通常在小电流下测量的60 Hz接地电阻。 如果已知土壤的临界电场，则可以估算任何给定脉冲电流的脉冲阻抗。 因此，对于接地系统设计以及雷电性能研究，必须有一个广义的土壤临界电场方程。 这里提出了土壤临界电场$E_c$的广义方程，它是土壤介电常数$k_g$和电导率$\sigma_g$的函数。 在不同的土壤，不同的水分含量下进行了广泛的脉冲测试和电气测量。 介电常数k g通过使用土壤填充的同轴传输线的波传播技术测量。 统计分析了波形对不同土壤临界电场$E_c$的影响。

1. 简介

先前的研究人员已经提出，如果已知土壤E c的临界电场，则可以准确估算接地棒的脉冲阻抗[1,2]。 然而，先前的研究报道了各种各样的E c值（70-2700 kV / m）[3-7]。 Oettle [4]建议E c值为1 MV / m。 但是，Mousa [6]观察到Oettle的结果在600–1850 kV / m的范围内变化，对于水分含量较高的土壤，其值较低（600–800 kV / m）。 Mousa进一步观察到，在雷暴天气和野外条件下，不均匀度要比实验室条件下高得多，Oettle结果的下限约为一半，即300-400 kV / m。 MousacitedLiew和Dayveniza [3]成功地使用临界电压为300 kV / m来模拟观察到的多个电极的动态行为。 因此，Mousa建议将300 kV / m用于典型土壤的临界电场。

由于土壤的电学特性因一种土壤类型而异，因此，$E_c$的单一值是不合理的。 因此，必须有适用于任何土壤类型的临界电场$E_c$的广义方程。

土壤的电参数是土壤电阻率$\rho_g$，介电常数$\varepsilon_g$（$\varepsilon_g = k_g \varepsilon_0$）和渗透率（$\mu_g = \mu_0 \mu_r$），其中空气中的$\mu_0$介电常数$varepsilon_0 = 8.854 \times 10^{-12}F/m$和$\mu_0 = 4 \pi \times 10^{-7}H/m$。 除非土壤中没有任何磁性材料，否则参数$\mu_g = \mu_0$。 据报道，频域测量土壤和岩石的介电常数和电阻率会随测量频率和水分含量的变化而显着变化[8-10]。 据报道，电容随着频率的增加呈指数下降。 电容测量中的误差是由极化效应引起的，极化效应与频率有关。 但是，由于脉冲电压或电流是时间相关的现象，因此接地系统的脉冲行为也是时间相关的现象。 因此，在时域内测量土壤电参数似乎更为合适。

这项研究的目的是根据不同类型土壤的广泛实验室测试结果，根据重要土壤参数$k_g$和$\sigma_g$提出土壤临界电场的广义表达式（$E_c$模型）。 统计分析了各种土壤中波形对临界电场$E_c$的重要性。

接地电极土壤电离模型的严格审查（A critical review on soil ionisation modelling for grounding electrodes）

DOI 10.1515/aee-2016-0033

摘要

由于土壤电离现象，在脉冲条件下接地电极电阻会非线性变化。 已经提出了几种模型来模拟用于接地电极应用的土壤电离。 但是，迄今为止，还没有尝试将所有这些作品汇编成一篇全面的评论文章。 因此，本文旨在总结该领域的所有相关著作，作为一站式参考。 参考文献，本文旨在总结土壤电离模型的工作原理以及模型的准确性和性能分析。 本文特别强调了可用模型在准确性和性能方面的不足。 这些知识将有助于开发新的准确有效的土壤电离模型。

1. 简介

当高冲击电流通过接地导体[1-5]排放到土壤中时，会发生土壤击穿现象。 由于土壤的破坏，土壤的电阻降低，因此接地电极的峰值电压响应降低。 因此，土壤击穿提高了接地系统的效率。 提出了两个主要过程来解释在高脉冲电流放电期间土壤传导的增加，即（1）热加热过程和（2）土壤电离过程。 在热加热过程中，放电电流会增加土壤颗粒中现有水的填充温度。 由于加热过程，热水的电阻率降低，这继而导致散装土壤的电阻率降低，从而降低了接地电极的电阻[6-8]。 在土壤电离过程中，土壤颗粒之间的空隙中的电场增强，导致土壤分解[5，9-11]。 由于电离空气的电阻远小于土壤颗粒的电阻，因此等效土壤电阻降低。 值得注意的是，土壤电离是土壤分解现象的主要因素。

已经提出了几种电路模型来模拟土壤电离及其对接地电极电阻的影响。 尽管在该领域进行了许多公开的研究，但似乎没有一份全面的评论文章可以对优缺点进行评估。 参考文献，撰写本综述论文时要谨记以下目标：（1）总结CIGRE [4]，Bellaschi等人提出的可用土壤电离模型的功能和工作原理。 [3]，Nor等。 [12]和Liew和Darveniza [13]和（2）在准确性，所用方法的复杂性和应用方面评估了所述土壤电离模型的优缺点。 在本文的最后，还提供了土壤电离模型与相应实验结果之间的比较。 本文的其余部分安排如下：

第2节介绍了介绍土壤电离过程和接地电极电阻特性的理论背景。 在第3节中，对土壤电离模型进行了严格审查。 第四部分讨论了土壤电离模型的准确性和性能分析。 最后，第5节给出了整体讨论和结论。

1. 从麦克斯韦方程组推导波动方程

其实导线和真空中电磁波的传播的波动方程是一致的，因为导线内并不存在电荷，整个导线是处于中性状态，故麦克斯韦方程组可以写为：

$\nabla \cdot E = 0\tag{1}$ $\nabla \cdot B = 0\tag{2}$ $\nabla \times E = - \frac { \partial B } { \partial t }\tag{3}$ $\nabla \times B = \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial E } { \partial t }\tag{4}$

对式（3）两边都去旋度。

$\nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E = - \frac { \partial } { \partial t } ( \nabla \times B )$

由于式（1），所以可以简写为

$0 - \nabla ^ { 2 } E = - \frac { \partial } { \partial t } ( \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial E } { \partial t } )$

这里用到一个矢量三重积公式：

$\nabla \times ( \nabla \times E ) = \nabla ( \nabla \cdot E ) - \nabla ^ { 2 } E$

最后，波动方程为：

$\nabla ^ { 2 } E = \mu _ { 0 } \varepsilon _ { 0 } \frac { \partial ^ { 2 } E } { \partial t ^ { 2 } }\tag{5}$

第一章

1. 世界初步展示
2. 冒险的召唤（可能主角有拒绝）
3. 越过第一道边界

第二章

1. 考验、伙伴和敌人
2. 接近最深的洞穴
3. 遭遇磨难

第三章

1. 返回的路
2. 大决战
3. 英雄复活
4. 携万能药归来