1. 分析实验中的电流谐波含量

做接地电力谐波分析。

爸爸和妈妈

这是平凡幕后的视频，袁代川拍的，看完后有很多感想。

1. 大家都很忙碌

   忙生活不易，挣钱不易，在有限的时间要出产一个精品的东西不易，所以需要忙碌起来。

2. 做事情规划很重要

   飞猪老师首先用文字编辑器将要说的话都写下来，然后用excel来做分镜脚本，这样在拍摄前能做到有的放矢。

3. 要动脑筋

   拍视频美很重要，设备很重要，但更重要的是要动脑筋，想给人描述清楚一个东西，要变化描述角度，常人接触到的内容是干涩的，是低级的，用低级的设备以及大脑去理解高级的东西就需要将高级的东西降低。比如去描述HDR，120Hz这个概念，常人用24Hz的影片观看效果是SDR，根本就不可能看出真正的HDR是什么意思，所以只能去类比。

   反过来想，只要将HDR和120Hz的东西拿出来给人家看，一对比就完全清楚了。

   但将概念低级化，讲出来还是有意义的。

4. 需求是人创造的

   一般人对HDR的概念不了解，或者以为自己了解，但没有真正去了解的冲动与勇气，这部分人只是觉得要了解这个信息付出的辛苦太多了而已，这时候如何将这个概念给他们，让这个概念成为他们的谈资，是自己的本事。

   反过来想，一般人都不会去努力了解这些东西，那么这些一般人不了解的东西就会成为自己的护城河。

朝阳里，她向我跑来，那笑容明亮的，让其他的一切都失去了神采。

朝阳里，我转身走开，她向我跑过来，眼里的惊慌失措和依依不舍。

https://weibo.com/tv/v/Iy7qauM6Q?fid=1034:4481315127623700

http://media.w3.org/2010/05/sintel/trailer.mp4

http://f.video.weibocdn.com/Vd1C8rlNlx07BCfb1cYE01041201qryo0E010.mp4?label=mp4_hd&template=852x480.25.0&trans_finger=1621fcd5d40969f1c74e6b06e52fcd54&Expires=1583923063&ssig=nxZ8wuRZ5K&KID=unistore,video

FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

以下步骤显示了如何在Level-2 MATLAB Sfunctions中初始化和使用DWork向量。 这些步骤使用S函数msfcn_unit_delay.m。

1. 在PostPropagationSetup方法中，初始化DWork向量的数量以及每个向量的属性。 例如，以下PostPropagationSetup回调方法配置一个DWork向量，用于存储离散状态。

    function PostPropagationSetup(block)
    %% Setup Dwork
    block.NumDworks = 1;
    block.Dwork(1).Name = 'x0';
    block.Dwork(1).Dimensions = 1;
    block.Dwork(1).DatatypeID = 0;
    block.Dwork(1).Complexity = 'Real';
    block.Dwork(1).UsedAsDiscState = true;
   

   Simulink.BlockCompDworkData和父类Simulink.BlockData的参考页列出了可以为Level-2 MATLAB Sfunction DWork向量设置的属性。

2. 在Start或InitializeConditions方法中初始化DWork向量值。 将Start方法用于仅在模拟开始时初始化的值。 每当重新启用包含S功能的已禁用子系统时，请使用InitializeConditions方法获取需要重新初始化的值。

   例如，下面的InitializeConditions方法将在上一步中配置的DWork向量的值初始化为第一个S函数对话框参数的值。

    function InitializeConditions(block)
    %% Initialize Dwork
    block.Dwork(1).Data = block.DialogPrm(1).Data;
   

3. 在“Outputs”，“Update”等方法中，根据需要使用或更新DWork矢量值。 例如，以下Outputs方法将S函数输出设置为等于DWork向量中存储的值。 然后，Update方法将DWork向量值更改为第一个S函数输入端口的当前值。

    %% Outputs callback method
    function Outputs(block)
    block.OutputPort(1).Data = block.Dwork(1).Data;
    %% Update callback method
    function Update(block)
    block.Dwork(1).Data = block.InputPort(1).Data;
   

2级MATLAB S函数不支持MATLAB稀疏矩阵。 因此，您不能将稀疏矩阵分配给DWork向量的值。 例如，以下代码行会产生错误 block.Dwork(1).Data = speye(10) speye命令生成一个稀疏的恒等矩阵。

一个常规的微分方程。

$\frac { d y } { d t } = a y + e ^ { s t }$ $y = y(0) at t = 0$ Look for $y_p = Ye^{st}$

把$\frac { d y } { d t }$比做银行的钱的增长率，$y$就是银行的利息，$e ^ { s t }$代表挣到的钱，是指数形式的，$s$代表souce，源，t代表时间。

带入$y_p = Ye^{st}$，得到$Y = \frac {1}{s-a}$

则 $y(t) = \frac{e^{st}}{s-a} + null solution$

null solution的意思是，输入项没有了，也就是$e^{st} = 0$，求$\frac { d y } { d t } = a y$，得$y = e^{at}$

所以，通解

$y(t) = \frac{e^{st}}{s-a} + Ce^{at} = y_p + y_n\tag{1}$

y_p意思是y_particular，y_n意思是y_null。

将$y = y(0) at t = 0$带入得特解

$y(0) = \frac {1}{s-a} + C$

则$C = y(0) - \frac {1}{s-a}$，带回（1）得，将y(0)单独提出来

$\begin{aligned} y ( t ) &\left. = \frac { e ^ { s t } } { s - a } + \left[ y ( 0 \right) - \frac { 1 } { s - a } \right] e ^ { a t } \ & = \frac { e ^ { s t - e ^ { a t } } } { s a } + y ( 0 ) e ^ { a t } \ & = y_{vp} + y_n \end{aligned}$

y_vp是y_very particular。

特接并不唯一。

这个null solution很好，可以看做是从初始状态开始的一个变化，并包含初始状态信息。

这个特别的解很好，有这样的性质，当t=0时，特解同时=0，这样就得到了通解。

但是有一个例外，当s=a时，分母为0，同时分子也为0，这时，就出现了震荡（Resonance）。这时候需要用到洛必达（L‘ Hopital）法则。

IF s = a，then

$y_{vp}+y_n = t e^{at} + y(0)e^{at}\tag{2}$

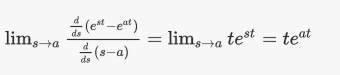
由此得到公式(2)中的特解部分。

test

如何给人分享一个东西让人家觉得珍贵，而自己又付出的较少。

利用迭代效应影响他人。

比如茶叶，普洱茶流传着一句至理名言，“越陈越香，越老越贵”。说的是茶存放的时间越长它的品质越好，相应的茶会升值。

利用这个效应来送礼就很合适，送的可以有时间的加成。

朋友请自己喝百茶堂的老茶，我们心里觉得这茶就很贵，很好，自然入喉后仔细的品味一番，然后就会不自然的说这是好茶。

而实际上，朋友买的时候的价格并没有特别贵重，这就是时间的味道。

反过来想问题就是，现在就要为未来请客积攒礼物，如何挑选越陈越值钱的礼物是很关键的，这个需要再仔细思量。

喝到一款很好喝的茶，而并不是百茶堂，忽有感，百茶堂的茶也并没有那么优秀，而在王晨那里喝到很好的茶，年份也好，但就不会觉得特别优秀，这就是如何营造时间的意义方面的话题了。